Деревья игры. Поиск выигрышной стратегии

Будем рассматривать класс игр двух лиц с полной информацией. В таких играх участвуют два игрока, которые поочередно делают свои ходы. В любой момент игры каждому игроку известно все, что произошло в игре к этому моменту и что может быть сделано в настоящий момент. Игра заканчивается либо выигрышем одного игрока (и проигрышем другого), либо ничьей.

Таким образом, в рассматриваемый класс не попадают игры, исход которых зависит хотя бы частично от случая − большинство карточных игр, игральные кости, «морской бой» и проч. Тем не менее класс достаточно широк: в него входят такие игры, как шахматы, шашки, реверси, калах, крестики-нолики и др.

Для формализации и изучения игровых стратегий в классе игр с полной информацией может быть использован подход, основанный на редукции задач. Напомним, что при этом должны быть определены следующие составляющие: форма описания задач и подзадач; операторы, сводящие задачи к подзадачам; элементарные задачи; а также задано описание исходной задачи.

Наиболее интересной представляется задача поиска выигрышной стратегии для одного из игроков, отправляясь от некоторой фиксированной конфигурации (позиции) игры (не обязательно начальной). При использовании подхода, основанного на редукции задач, выигрышная стратегия ищется в процессе доказательства того, что игра может быть выиграна. Аналогично, поиск ничейной стратегии, исходя из некоторой конкретной позиции, ведется в процессе доказательства того, что игра может быть сведена к ничьей.

Ясно, что описание решаемой задачи должно содержать описание конфигурации игры, для которой ищется нужная стратегия. Например, в шашках игровая позиция включает задание положений на доске всех шашек, в том числе дамок. Обычно описание конфигурации содержит также указание, кому принадлежит следующий ход.

Пусть именами игроков будут ПЛЮС и МИНУС. Будем использовать следующие обозначения:

X^S (или Y^S) − некоторая конфигурация игры, причем индекс S принимает значения + или −, указывая тем самым, кому принадлежит следующий ход (т.е. в конфигурации X⁺ следующий ход должен делать игрок ПЛЮС, а в X⁻ – игрок МИНУС);

W(X^S) − задача доказательства того, что игрок ПЛЮС может выиграть, исходя из конфигурации X^S;

V(X^S) − задача доказательства того, что игрок МИНУС может выиграть, отправляясь от конфигурации X^S.

Рассмотрим сначала игровую задачу W(X^S). Операторы сведения этой задачи к подзадачам определяются исходя из ходов, допустимых в проводимой игре:

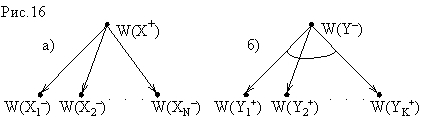
Если в некоторой конфигурации X⁺ очередь делать ход за игроком ПЛЮС, и имеется N допустимых ходов, приводящих соответственно к конфигурациям X₁⁻, X₂⁻, . . . X_N⁻ , то для решения задачи W(X⁺) необходимо решить по крайней мере одну из подзадач W(X_i⁻) (так как ход выбирает ПЛЮС, то он выиграет игру, если хотя бы один из ходов ведет к выигрышу) − см. рис. 16(а).
Если же в некоторой конфигурации Y⁻ ход должен сделать МИНУС, и имеется K допустимых ходов, приводящих к конфигурациям Y₁⁺ , Y₂⁺ , . . . Y_K⁺, то для решения задачи W(Y⁻) требуется решить каждую из возникающих подзадач W(Y_i⁺) (так как ход выбирает МИНУС, то ПЛЮС выиграет игру, если выигрыш гарантирован ему после любого хода противника) − см. рис. 16(б).

Последовательное применение для исходной конфигурации игры данной схемы сведения игровых задач к совокупности подзадач порождает И/ИЛИ-дерево (И/ИЛИ-граф), которое называют деревом (графом) игры. Дуги игрового дерева соответствуют ходам игроков, вершины − конфигурациям игры, причем листья дерева − это позиции, в которых игра завершается выигрышем, проигрышем или ничьей. Часть листьев являются заключительными вершинами, соответствующими элементарным задачам − позициям, выигрышным для игрока ПЛЮС. Заметим, что для конфигураций, где ход принадлежит ПЛЮСу, в игровом дереве получается ИЛИ-вершина, а для позиций, в которых ходит МИНУС, − И-вершина.

Цель построения игрового дерева или графа − получение решающего поддерева (подграфа) для задачи W(X^S), показывающего, как игрок ПЛЮС может выиграть игру из позиции X^S независимо от ответов противника. Для этого могут быть применены разные алгоритмы поиска на И/ИЛИ-графах. Решающее дерево или граф заканчивается на позициях, выигрышных для ПЛЮСа, и содержит полную стратегию достижения им выигрыша: для каждого возможного продолжения игры, выбранного противником, в дереве или графе есть ответный ход, приводящий к победе.

Для задачи V(X^S) схема сведения игровых задач к подзадачам аналогична: ходам игрока ПЛЮС будут соответствовать И-вершины, а ходам МИНУСа − ИЛИ-вершины, заключительные же вершины будут соответствовать позициям, выигрышным для игрока МИНУС.

Конечно, подобная редукция задач применима и в случае, когда нужно доказать существование ничейной стратегии в игре. При этом определение заключительной вершины (элементарной задачи) должно быть соответствующим образом изменено.

В большинстве игр, представляющих интерес, таких как шашки и шахматы, построить полные решающие деревья или графы (и найти полные игровые стратегии) не представляется возможным. Например, для шашек число вершин в полном игровом дереве оценивается величиной порядка 10⁴⁰, и просмотреть такое дерево практически нереально. Алгоритмы же упорядоченного перебора с применением эвристик не настолько уменьшают просматриваемую часть дерева игры, чтобы дать существенное (на несколько порядков) сокращение времени поиска.

Тем не менее в случае неполных игр в шашки и шахматы (например, для эндшпилей), так же как и для всех несложных игр, таких как «крестики-нолики» на фиксированном квадрате небольшого размера, можно успешно применять алгоритмы поиска на И/ИЛИ-графах, позволяющие обнаруживать выигрышные и ничейные игровые стратегии.

Рассмотрим, к примеру, игру «крестики-нолики» на квадрате 3×3. Игрок ПЛЮС ходит первым и ставит крестики, а МИНУС − нолики. Игра заканчивается, когда составлена либо строка, либо столбец, либо диагональ из крестиков (выигрывает ПЛЮС) или ноликов (выигрывает МИНУС). Оценим размер полного дерева игры: начальная вершина имеет 9 дочерних вершин, каждая из которых в свою очередь − 8 дочерних; каждая вершина глубины 2 имеет 7 дочерних и т.д. Таким образом, число концевых вершин в дереве игры равно 9!=362880, но многие пути в этом дереве обрываются раньше на заключительных вершинах. Значит, в этой игре возможен полный просмотр дерева и нахождение выигрышной стратегии. Однако ситуация изменится при существенном увеличении размеров квадрата или в случае неограниченного поля игры.

В таких случаях, как и во всех сложных играх вместо нереальной задачи поиска полной игровой стратегии решается, как правило, более простая задача − поиск для заданной позиции игры достаточно хорошего первого хода.