Альфа-бета процедура
Минимаксная процедура организована таким образом, что процесс построения частичного дерева игры отделен от процесса оценивания вершин. Такое разделение приводит к тому, что в целом минимаксная процедура − неэффективная стратегия поиска хорошего первого хода. Чтобы сделать процедуру более экономной, необходимо вычислять статические оценки концевых вершин и минимаксные оценки промежуточных вершин одновременно с построением игрового дерева. Этот путь приводит к так называемой альфа-бета процедуре поиска наилучшего первого хода от заданной позиции, на нем можно добиться существенного сокращения вычислительных затрат, прежде всего, времени вычисления оценок. В основе такого сокращения поиска лежит достаточно очевидное соображение: если есть два варианта хода одного игрока, то худший в ряде случаев можем сразу отбросить, не выясняя, насколько в точности он хуже.
Рассмотрим сначала идею работы альфа-бета процедуры на примере игрового дерева, приведенного на рис.19. Дерево игры строится до глубины N=3 алгоритмом перебора вглубь. Причем сразу, как это становится возможным, вычисляются не только статические оценки концевых вершин, но и предварительные минимаксные оценки промежуточных вершин. Предварительная оценка определяется соответственно как минимум или максимум уже известных (к настоящему моменту) оценок дочерних вершин, и она может быть получена при наличии оценки хотя бы одной дочерней вершины. Предварительные оценки затем постепенно уточняются по минимаксному принципу – по мере получения новых (предварительных и точных) оценок в ходе дальнейшего построения дерева.
Пусть таким образом построены вершины W1−, W2+ и первые три конечные вершины (листья) − см. рис.20. Эти листья оценены статической функцией, и вершина W2+ получила точную минимаксную оценку 3, а вершина W1− − предварительную оценку 3. Далее при построении и раскрытии вершины W3+ статическая оценка первой ее дочерней вершины дает величину 4, которая становится предварительной оценкой самой вершин W3+ . Эта предварительная оценка будет потом (после построения второй дочерней вершины) пересчитана, причем согласно минимаксному принципу она может только увеличиться (так как равна максимуму оценок дочерних вершин), но даже если она увеличится, это не повлияет на оценку вершины W1−, поскольку последняя при уточнении по минимаксному принципу может только уменьшаться (она равна минимуму оценок дочерних вершин). Следовательно, можно пренебречь второй дочерней вершиной для W3+, не строить и не оценивать ее (так как уточнение оценки вершины W3+ не повлияет на оценку вершины W1−). Такое сокращение процедуры поиска в дереве называется отсечением ветвей дерева.
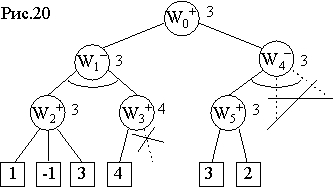
Продолжим для нашего примера процесс поиска в глубину с одновременным вычислением предварительных (и точных, где это возможно) оценок вершин вплоть до момента, когда построены уже вершины W4− , W5+ и две дочерних последней, которые оцениваются статической функцией. Исходя из оценки первой дочерней вершины начальная вершина W0+, соответствующая исходной позиции игры, к этому моменту уже предварительно оценена величиной 3. Вершина W5+ получила точную минимаксную оценку 3, а ее родительская W4− получила пока только предварительную оценку 3. Эта предварительная оценка вершины W4−может быть уточнена в дальнейшем, но в соответствии с минимаксным принципом возможно только ее уменьшение, а это уменьшение не повлияет на оценку вершины W0+, поскольку последняя, опять же согласно минимаксному принципу, может только увеличиваться. Таким образом, построение дерева можно прервать ниже вершины W4−, отсекая целиком выходящие из нее вторую и третью ветви (и оставляя ее оценку предварительной).
На этом построение рассматриваемого игрового дерева заканчивается, полученный результат − лучший первый ход − тот же самый, что и при минимаксной процедуре. У некоторых вершин дерева осталась неуточненная, предварительная оценка, однако этих приближенных оценок оказалось достаточно для того, чтобы определить точную минимаксную оценку начальной вершины и наилучший первый ход. В то же время произошло существенное сокращение поиска: вместо 17 вершин построено только 11, и вместо 10 обращений к статической оценочной функции понадобилось всего 6.
Обобщим рассмотренную идею сокращения перебора. Сформулируем сначала правила вычисления оценок вершин дерева игры, в том числе предварительных оценок промежуточных вершин, которые для удобства будем называть альфа- и бета-величинами:
- концевая вершина дерева оценивается статической оценочной функцией сразу, как только она построена;
- промежуточная вершина предварительно оценивается по минимаксному принципу, как только стала известна оценка хотя бы одной из ее дочерних вершин; каждая предварительная оценка пересчитывается (уточняется) всякий раз, когда получена оценка еще одной дочерней вершины;
- предварительная оценка ИЛИ-вершины (альфа-величина) полагается равной наибольшей из вычисленных к текущему моменту оценок ее дочерних вершин;
- предварительная оценка И-вершины (бета-величина) полагается равной наименьшей из вычисленных к текущему моменту оценок ее дочерних вершин.
Укажем очевидное следствие этих правил вычисления: альфа-величины не могут уменьшаться, а бета-величины не могут увеличиваться.
Сформулируем теперь правила прерывания перебора, или отсечения ветвей игрового дерева:.
1. Перебор можно прервать ниже любой И-вершины, бета-величина которой не больше, чем альфа-величина одной из предшествующих ей ИЛИ-вершин (включая корневую вершину дерева);
2. Перебор можно прервать ниже любой ИЛИ-вершины, альфа-величина которой не меньше, чем бета-величина одной из предшествующих ей И-вершин.
При этом в случае А говорят, что имеет место альфа-отсечение (поскольку отсекаются ветви дерева, начиная с ИЛИ-вершин, которым приписана альфа-величина), а в случае В − бета-отсечение (поскольку отсекаются ветви, начинающиеся с бета-величин).
Важно, что рассмотренные правила работают в ходе построения игрового дерева вглубь; это означает, что предварительные оценки промежуточных вершин появляются лишь по мере продвижения от концевых вершин дерева вверх к корню и реально отсечения могут начаться только после того, как получена хотя бы одна точная минимаксная оценка промежуточной вершины.
В рассмотренном примере на рис. 20 первое прерывание перебора было бета-отсечением, а второе − альфа-отсечением. Причем в обоих случаях отсечение было неглубоким, поскольку необходимая для соблюдения соответствующего правила отсечения предварительная оценка (альфа- или бета-величина) находилась в непосредственно предшествующей (к точке отсечения) вершине. В общем же случае она может находиться существенно выше отсекаемой ветви – на пути от вершины, ниже которой производится отсечение, к начальной вершине, включая последнюю.
После прерывания перебора предварительные оценки вершин в точках отсечения остаются неуточненными, но, как уже отмечалось, это не препятствует правильному нахождению предварительных оценок всех предшествующих вершин, как и точной оценки корневой вершины и ее дочерних вершин, а значит, и искомого наилучшего первого хода.
На приведенных выше правилах вычисления оценок вершин и выполнения отсечений (всюду, где это возможно) основана альфа-бетапроцедура, являющаяся более эффективной реализацией минимаксного принципа. Несложно в принципе, используя математическую индукцию и рассуждая аналогично рассмотренному примеру, доказать следующее
Утверждение:
Альфа-бета процедура всегда приводит к тому же результату (наилучшему первому ходу), что и простая минимаксная процедура той же глубины.
Важным является вопрос, насколько в среднем альфа-бета процедура эффективнее обычной минимаксной процедуры. Нетрудно заметить, что количество отсечений в альфа-бета процедуре зависит от степени, в которой полученные первыми предварительные оценки (альфа- бета-величины) аппроксимируют окончательные минимаксные оценки: чем ближе эти оценки, тем больше отсечений и меньше перебор. Это положение иллюстрирует пример на рис.20, в котором основной вариант игры обнаруживается практически в самом начале поиска.
Таким образом, эффективность альфа-бета процедуры зависит от порядка построения и раскрытия вершин в дереве игры. В принципе возможен и неудачный порядок просмотра, при котором придется пройти (без отсечений) через все вершины дерева, и в этом, худшем случае, альфа-бета процедура не будет иметь никаких преимуществ против минимаксной процедуры.
Наилучший случай (наибольшее число отсечений) достигается, когда при переборе в глубину первой обнаруживается конечная вершина, статическая оценка которой станет в последствии минимаксной оценкой начальной вершины. При максимальном числе отсечений требуется строить и оценивать минимальное число концевых вершин. Показано, что в случае, когда самые сильные ходы всегда рассматриваются первыми, количество концевых вершин глубины N, которые будут построены и оценены альфа-бета процедурой, примерно равно числу концевых вершин, которые были бы построены и оценены на глубине N/2 обычной минимаксной процедурой. Таким образом, при фиксированном времени и памяти альфа-бета процедура сможет пройти при поиске вдвое глубже по сравнению с обычной минимаксной процедурой.
В заключение отметим, что статическая оценочная функция и альфа-бета процедура − две непременные составляющие подавляющего большинства компьютерных игровых программ (в том числе коммерческих). Часто используются также дополнительные эвристические приемы в самой альфа-бета процедуре:
- направленное (эвристическое) отсечение неперспективных ветвей (например, построение дерева игры обрывается на «пассивных» позициях, к которым применяется оценочная функция, для «активных» же позиций поиск продолжается дальше, до нужной глубины или даже глубже, поскольку на это можно использовать время, сэкономленное вследствие отбрасывания ветвей);
- последовательное углубление, при котором альфа-бета процедура применяется неоднократно: сначала до некоторой небольшой глубины (например, 2), а затем глубина увеличивается с каждой итерацией, причем после каждой итерации выполняется переупорядочение всех дочерних вершин – с тем, чтобы увеличить число отсечений в последующих итерациях;
- фиксированное упорядочение вершин при спуске-построении дерева вглубь, при котором в первую очередь строится и раскрывается дочерняя вершина, оцениваемая как более перспективная (эта оценка может быть проведена как с помощью статической оценочной функции, так и более простой, хотя и менее надежной эвристической функции);
- динамическое упорядочение вершин, при котором каждый раз после уточнения минимаксных оценок и проведения отсечений производится переупорядочивание вершин во всем построенном к текущему моменту дереве (с помощью некоторой эвристической функции) и для дальнейшего раскрытия выбирается наиболее перспективная вершина (по существу это означает переход от классического перебора вглубь к алгоритму упорядоченного перебора на И/ИЛИ-графах).
Для усиления игры могут быть также использованы библиотека типовых игровых ситуаций и другие идеи.