рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Компьютеры
- /
- Поиск экстремума функции средствами MathCad
Реферат Курсовая Конспект
Поиск экстремума функции средствами MathCad
Поиск экстремума функции средствами MathCad - раздел Компьютеры, Гартман Т. Н., Клушин Д. В. Основы компьютерного моделирования химико-технологических процессов Задачи Поиска Экстремума Функции Означают Нахождение Ее Максимума (Наибольшег...
Задачи поиска экстремума функции означают нахождение ее максимума (наибольшего значения) или минимума (наименьшего значения) в некоторой области определения ее аргументов. Ограничения значений аргументов, задающих эту область, как и прочие дополнительные условия, должны быть определены в виде системы неравенств и (или) уравнений. В таком случае говорят о задаче на условный экстремум.
Для решения задач поиска максимума и минимума в Mathcad имеются встроенные функции Minerr, Minimize и Maximize.
Экстремум функции одной переменной
Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. Последние называют еще задачами оптимизации. Рассмотрим конкретный пример функции f(x), показанной графиком на рис. 4 на интервале (-2,5). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальный минимум и локальный максимум на правой границе интервала (в порядке слева направо).
В Mathcad с помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканировать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последний путь таит в себе некоторую опасность уйти в зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономии времени.

Рис. 4. График функции f(х)=х4+5х3-10х
Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.
Minimize (f, x1, ... ,хм) — вектор значений аргументов, при которых функция f достигает минимума;
Maximize (f, х1, ... ,хм) — вектор значений аргументов, при которых функция f достигает максимума;
f (x1,...,хм,...) — функция;
x1,...,xм — аргументы, по которым производится минимизация (максимизация).
Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления экстремума функции одной переменной (рис. 4) без дополнительных условий показаны ниже. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняется для любых значений.
Минимум функции одной переменной.
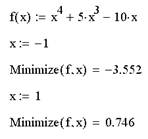
Максимум функции одной переменной.

Как видно из примеров, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются различные локальные экстремумы. В последнем случае численный метод вообще не справляется с задачей, поскольку начальное приближение х=-10 выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения f (х).
Условный экстремум
В задачах на условный экстремум функции минимизации и максимизации должны быть включены в вычислительный блок, т. е. им должно предшествовать ключевое слово Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логические выражения (неравенства, уравнения), задающие ограничения на значения аргументов минимизируемой функции. Ниже показаны примеры поиска условного экстремума на различных интервалах, определенных неравенствами.

Не забывайте о важности выбора правильного начального приближения и в случае задач на условный экстремум. Например, если вместо условия -3<х<0 в последнем примере задать
-5<х<0, то при том же самом начальном х=-10 будет найден максимум Maximize(f,x) =-0.944, что неверно, поскольку максимальное значение достигается функцией f (х) на левой границе интервала при х=-5. Выбор начального приближения х=-4 решает задачу правильно, выдавая в качестве результата Maximize (f ,x) =-5.
Экстремум функции многих переменных
Вычисление экстремума функции многих переменных не несет принципиальных особенностей по сравнению с функциями одной переменной. Поэтому ограничимся примером нахождения максимума и минимума функции, показанной в виде графиков трехмерной поверхности и линий уровня на рис. 5.
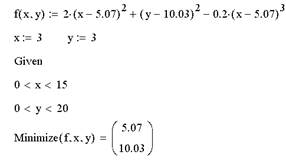
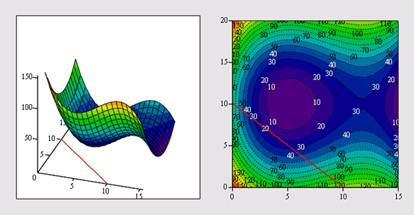
Рис. 5. График функции f (х, у) и отрезок прямой х+у=10
Дополнительные условия могут быть заданы и равенствами. Например, определение после ключевого слова Given уравнения х+у=10 приводит к такому решению задачи на условный экстремум.
Как нетрудно сообразить, еще одно дополнительное условие привело к тому, что численный метод ищет минимальное значение функции f(x,y) вдоль отрезка прямой, показанного на рис. 5.
Поиск минимума можно организовать и с помощью функции Minerr. Для этого в примере надо поменять имя функции Minimize на Minerr, а после ключевого слова Given добавить выражение, приравнивающее функции f(х,у) значение, заведомо меньшее минимального, например f (х,у)=0.
Тема 5. Формализованные модели химически активных газовых систем
Модель формализованного стехиометрического реактора.
 Рассмотрим одностадийный стехиометрический реактор, в котором имеет место одностадийная химическая реакция. В общем случае хим реакция м б описана стехиометрическим уравнением
Рассмотрим одностадийный стехиометрический реактор, в котором имеет место одностадийная химическая реакция. В общем случае хим реакция м б описана стехиометрическим уравнением
m1A1+m2A2+…+mnAn = r1B1+r2B2+…+rlBl+In
Тогда уравнение материального баланса для этой реакции можно записать как

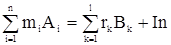 , (1)
, (1)
где n – количество исходных веществ; l – количество конечных веществ; In – инерты; mi, ri – стехиометрические коэффициенты; Аi, Bk – исходные и конечные вещества.
Из стехиометрического уравнения следует, что количество вступающих во взаимодействие веществ относятся как их стехиометрические коэффициенты.
 ;
; 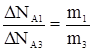 ;
; 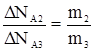 , (2)
, (2)
где DNi – изменение числа моль веществ.
Степень превращения целевого компонента (как правило, того который в недостатке)
 , (3)
, (3)
где N0i, Ni – начальное и конечное количество вещества i-го компонента.
В качестве целевого компонента выберем компонент А, тогда
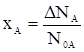 , (4)
, (4)
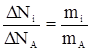 , (5)
, (5)
откуда
 , (6)
, (6)
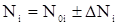 , (7)
, (7)
+ - для конечных веществ, - - для исходных.
В (7) подставляем (6) с учетом (4) и получаем
 , (8)
, (8)
 . (9)
. (9)
Концентрации исходных и конечных веществ можно определить по формулам:
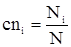 , (10)
, (10)
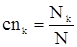 . (11)
. (11)
Общее количество вещества равно сумме общих количеств веществ начальных, конечных и инертов:
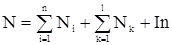 . (12)
. (12)
Общее количество начальных и конечных веществ можно вычислить по формулам:
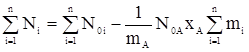 , (13)
, (13)
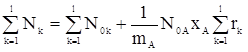 . (14)
. (14)
Тогда формулу (12) перепишем в виде
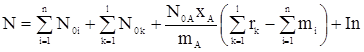 . (15)
. (15)
Обозначим через N0 сумму 1, 2 и последнего слагаемых в формуле (15):
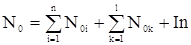 . (16)
. (16)
Обозначим через Dn выражение в скобках в формуле (15).
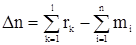 , (17)
, (17)
тогда (15) перепишем в виде
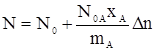 . (18)
. (18)
Модель формализованного стехиометрического реактора будетс состоять из следующих математических выражений:
 , (19)
, (19)
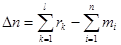 , (20)
, (20)
 , (21)
, (21)
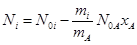 , (22)
, (22)
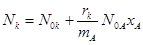 , (23)
, (23)
 , (24)
, (24)
 . (25)
. (25)
При моделировании формализованного стехиометрического реактора в качестве исходных варьируемых параметров целесообразно выбрать:
– количество конечных и исходных веществ (n, l);
– стехиометрические коэффициенты конечных и исходных веществ (rk, mi);
– начальные количества веществ N0i и инертов In;
– степень превращения хА.
К конечным данным: концентрации (cni, cnk), количество веществ на выходе (Ni, Nk)
К промежуточным параметрам следует отнести все остальные.
Программа, реализующая эту модель в Mathcad, должна состоять из блоков:
- Блок инициализации исходных параметров.
- Блок математической модели.
- Блок вывода результатов моделирования.
- Блок графической интерпретации результатов моделирования.
Модели идеального и реального газов.
В физике под идеальным газом понимается газ, в котором молекулы сводятся к точкам, взаимодействие между молекулами малы, поэтомусилами притяжения и отталкивания пренебрегают, взаимодействие молекул упругое. По своей сути идеальный газ – это модель реального газа, в которой приняты вышеперечисленные допущения.
Уравнением состояния называется уравнение, связывающее давление, объем и температуру формулой
 , (26)
, (26)
Самый простой вид уравнение имеет для идеального газа (уравн Менделеева-Клапейрона)
 , (27)
, (27)
Газ, подчиняющийся уравнению состояния  , называется идеальным. Все газы при достаточно низких давлениях являются идеальными.
, называется идеальным. Все газы при достаточно низких давлениях являются идеальными.
При расчетах объемов газов в условиях повышенных давлений уравнение () приводит к большим ошибкам.
Для описания реальных свойств газов было предложено много различных уравнений состояния. В 1948 году сводка уравнений состояния насчитывала их более 150. Первая попытка дать уравнение реального газа принадлежит Хирну (1867 г.):
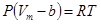 , (28)
, (28)
где b – константа, так называемый к-объем, имеет размерность объема.
Дальнейшее усложнение введено Ван-дер-Ваальсом в уравнении:
 , (29)
, (29)
где a – вторая константа, учитывающая взаимодействие между молекулами; Vm – молярный объем; b – поправка на объем, занимаемый молекулами, учитывает действие сил отталкивания. Константы a и b имеют теоретическое объяснение, но считаются эмпирическими.
Постоянные a и b рассчитываются из выражений:
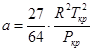 , (30)
, (30)
 , (31)
, (31)
где Pкр, Tкр – соответственно критические температура и давление.
Основное внимание уделяется уравнениям состояния, которые наиболее удобны для систем расчета свойств на ЭВМ.
Однако следует отметить, что вести расчеты по приведенным уравнениям следует с осторожностью, т.к. для каждого газа существует свой определенный интервал давлений и температур, за пределами которого данное уравнение может привести к значительным ошибкам. По сути, все предложенные уравнения состояния являются модификацией простого выражения 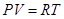 и уравнения Ван-дер-Ваальса.
и уравнения Ван-дер-Ваальса.
Одним из наиболее значительных достоинств рассмотренного ранее уравнения Ван-дер-Ваальса является количественное описание с его помощью критического состояния и явления сжижения газов.
Для каждого газа или пара имеется определенная температура, выше которой вещество не может быть сжижено одним давлением. Эта температура называется критической.
Критическая температура (Tкр) – это наивысшая температура, при которой газ может быть сжижен давлением.
Наинизшее давление, еще производящее сжижение, называется критическим давлением (Pкр). Удельный объем вещества при критическом давлении и критической температуре называется критическим объемом.
Критические температура, давление и объем представляют собой три широко используемые константы чистых веществ.
В табл. 1 приведены критические свойства некоторых веществ, встречающихся наиболее часто в технологии неорганических веществ.
Если выражать свойства газов и жидкостей не через P, V, T, а с помощью безразмерных единиц – приведенных параметров:
 ,
, 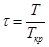 ,
,  , (32)
, (32)
то можно получить приведенное уравнение состояния:
 . (33)
. (33)
 . (34)
. (34)
Таблица 1
Физические свойства некоторых промышленных газов
| Газ | Молеку-лярная масса | Критические параметры | zкр | Нормальная температура плавления, | Нормальная температура кипения, | Теплота парообразо-вания при норм. | ||
| Tкр, К | Pкр, ат | Vкр, см3/моль | К | К | темп-ре, кал/моль | |||
| Аргон Ar | 39,948 | 150,8 | 48,1 | 74,9 | 0,291 | 83,8 | 87,3 | |
| Хлор Cl2 | 70,906 | 0,275 | 172,2 | 238,7 | ||||
| Водород H2 | 2,016 | 33,2 | 12,8 | 65,0 | 0,305 | 14,0 | 20,4 | |
| Вода Н2О | 18,015 | 647,3 | 217,6 | 56,0 | 0,229 | 273,2 | 373,2 | |
| Сульфид водорода H2S | 34,08 | 373,2 | 88,2 | 98,5 | 0,284 | 187,6 | 212,8 | |
| Аммиак NH3 | 17,031 | 405,6 | 111,3 | 72,5 | 0,242 | 195,4 | 239,7 | |
| Диоксид азота NO2 | 46,006 | 431,4 | 100,0 | 170,0 | 0,480 | 261,9 | 294,3 | |
| Азот N2 | 28,013 | 128,2 | 33,5 | 89,5 | 0,290 | 63,3 | 77,4 | |
| Гелий He | 4,003 | 5,19 | 2,24 | 57,3 | 0,301 | - | 4,21 | |
| Кислород O2 | 31,999 | 154,6 | 49,8 | 73,4 | 0,288 | 54,4 | 90,2 | |
| Диоксид серы SO2 | 64,063 | 430,8 | 77,8 | 122,0 | 0,268 | 197,7 | 263,0 | |
| Монооксид углерода CO | 28,010 | 132,9 | 34,5 | 93,1 | 0,295 | 68,1 | 81,7 | |
| Диоксид углерода CO2 | 44,010 | 304,2 | 72,8 | 94,0 | 0,274 | 216,6 | 194,7 | |
| Метан CH4 | 16,043 | 190,6 | 45,4 | 99,0 | 0,288 | 90,7 | 111,7 | |
| Метанол CH3OH | 32,042 | 512,6 | 79,9 | 118,0 | 0,224 | 175,5 | 337,8 | |
| Этилен C2H4 | 28,054 | 282,4 | 49,7 | 129,0 | 0,276 | 104,0 | 169,4 | |
| Пропан C3H8 | 44,097 | 369,8 | 41,9 | 203,0 | 0,281 | 85,5 | 231,1 |
Термодинамический реактор.
Физическая модель т/д реактора представляет собой смесь реагирующих газов. В данном случае выбираем ее в качестве объекта исследования.
Т/д система (ТДС) – любое макроскопическое тело, свойства которго исследуются. ТДС – это формализованная модель любого ХТП, в нашем случае – 2-я ступень иерархии при декомпозиции ХТП.
В конечном счете нас интересует степень превращения, которая возможна в данной системе химически активных газов с точки зрения термодинамики.
Согласно формуле (26) можно выделить три парметра состояния: Р, V, Т. Таким образом, степень превращения можно выразить как функцию этих трех параметров
 , (35)
, (35)
Представленное уравнение является формализованной моделью смеси реагирующих газов, поэтому объем можно заменить начальными концентрациями исходных и конечных веществ
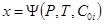 , (36)
, (36)
Температуру можно заменить константой равновесия Kf.
Моделирование энтальпии, энтропии, энергии Гиббса химического превращения.
Мерой самопроизвольного протекания хим процесса является изобарно-изотермический потенциал (функция Гиббса):
DGT0=DHT0-TDST0, (37)
Реакция может протекать в прямом направлении самопроизвольно при DG<0. Этому благоприятствует DН<0, DS>0. Чем более экзотермична реакция при данной температуре, тем вероятнее ее протекание.
DН – тепловой эффект реакции определяется на основании закона Гесса: тепловой эффект реакции равен сумме теплот образования продуктов реакции за вычетом суммы теплот образования исходных веществ с учетом с/х/м коэфф реагентов:
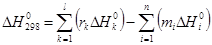 , (38)
, (38)
где 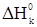 ,
, 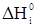 - стандартные энтальпии образования конечных и исходных веществ, кДж/моль (в спарвочной литературе).
- стандартные энтальпии образования конечных и исходных веществ, кДж/моль (в спарвочной литературе).
Если необходимо определить тепловой эффект реакции при температуре отличной от 298 К, то необходимо использовать уравнение Кирхгофа:
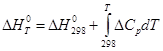 , (39)
, (39)
DСр – изменение теплоемкостей участников реакции.
DS – изменение энтропии в реакции, Дж/(моль×К).
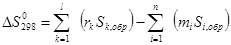 . (40)
. (40)
Если необходимо определить DS реакции при температуре отличной от 298 К, то необходимо использовать уравнение:
 , (41)
, (41)
Установлены эмпирические (интерполяционные) зависимости CP=f(T) в виде степенных рядов, которые приведены в справочных таблицах [см. Краткий справочник физико-химических величин].
Для неорганических веществ, Дж/(моль×К):
 , (42)
, (42)
Для органических веществ, Дж/(моль×К):
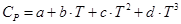 , (43)
, (43)
В этих уравнениях а, b, c, 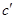 , d - эмпирические коэффициенты, справедливые для заданного интервала температур, приводимы в справочной литературе.
, d - эмпирические коэффициенты, справедливые для заданного интервала температур, приводимы в справочной литературе.
Тогда
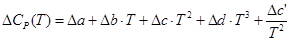 , (44)
, (44)
где
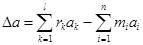 , (45)
, (45)
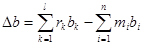 , (46)
, (46)
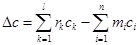 , (47)
, (47)
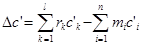 , (48)
, (48)
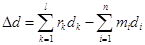 . (49)
. (49)
Таким образом, модель изменения теплоемкости в ходе реакции состоит из уравнений (45)-(49) и (44). Модель энтальпии реакции состоит из уравнений (38), (39), дополненных моделью изменения теплоемкости в ходе реакции. Модель энтропии реакции состоит из уравнений (40), (41), дополненных моделью изменения теплоемкости в ходе реакции. Модель изменения энергии Гиббса в ходе реакции состоит из уравнений модели изменения теплоемкости, энтальпии, энтропии, дополненных (37).
Формализация позволяет выделить следующие исходные данные: стехиометрические коэффициенты, коэффициенты, входящие в уравнение теплоемкости, количество исходных и конечных веществ, стандартные энетальпии и энтропии образования веществ, температура.
Необходимо учитывать, что энтальпии выражаеютя в кДж/моль, а теплоемкости и энтропии в Дж/(моль×К).
Математическое моделирование константы химического равновесия.
Для газов можно рассчитать константу равновесия по уравнению изотермы Вант-Гоффа:
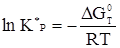 . (50)
. (50)
Изменение энергии Гиббса определяют по модели (37).
Таким образом модель константы химического превращения включает в себя модель изменения энергии Гиббса в ходе реакции, модели изменения теплоемкости, энтальпии, энтропии.
Математическая модель термодинамической сжимаемости.
Неидеальность газа можно выразить добавлением в уравнения состояния идеального газа (27) и (29) коэффициента сжимаемости z:
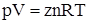 . (51)
. (51)
 для 1кмоль, (52)
для 1кмоль, (52)
Коэффициент сжимаемости z – это безразмерная величина, показывающая степень отклонения данного газа от идеального состояния. Для и.г. z=1. При известном значении z для данного газа можно рассчитать параметры состояния этого реального газа: p, T, V. Способ определения коэффициента z зависит от природы газа:
1) Определение величины z по индивидуальным графикам или уравнениям состояния. Для некоторых газов, свойства которых существенно зависят от межмолекулярного взаимодействия и от размера самих молекул, наблюдается резко индивидуальная зависимость z от р (рис. 1).
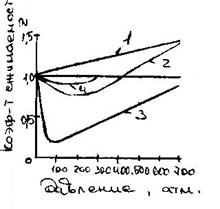
Рис. 1. Зависимость коэффициента сжимаемости от давления: 1 – водород, 2 – метан, 3 – аммиак, 4 – кислород.
Кроме газов, указанных на графике, не подчиняется общим закономерностям коэффициент сжимаемости для гелия, неона, сильно полярных газов (Н2О, НF).
2). Определение z по его зависимости от приведенных параметров π, τ и zк.
Величина zк называется критическим коэффициентом сжимаемости и вычисляется для состояния вещества в критической точке по формуле:
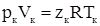 . (53)
. (53)
Для разработки математической модели можно воспользоваться известным уравнением состояния реального газа Редлих-Квонга:
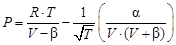 . (54)
. (54)
Экспериментальная константа a учитывает действие сил притяжения молекул, а константа b – эффективный молекулярный объем (действие сил отталкивания молекул). Константы a и b для i-го вещества выражаются через его индивидуальные опытные критические свойства ТКР, РКР:
 ; (55)
; (55)
 . (56)
. (56)
Необходимо всегда обращать внимание на то, что правильность количественного расчета зависит от единиц, в которых измеряются параметры уравнения состояния. В уравнениях (54)–(56) давление измеряется в физических атмосферах (атм), температура – в Кельвина (К), универсальная газовая постоянная R имеет единицу измерения  .
.
Для одновременного учета и критических параметров, и технологических параметров целесообразно ввести безразмерные факторы – приведенные температуры  и приведенные давления Рri. Математическая модель термодинамической сжимаемости для индивидуальных газов имеет весьма компактный вид:
и приведенные давления Рri. Математическая модель термодинамической сжимаемости для индивидуальных газов имеет весьма компактный вид:
 , (57)
, (57)
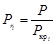 , (58)
, (58)
 , (59)
, (59)
 . (60)
. (60)
Система уравнений (57)–(60) является формализованной моделью термодинамической сжимаемости реальных газов.
При разработке программного модуля для расчета термодинамической сжимаемости требуется использование итерационного алгоритма. В среде MathCAD итерационный алгоритм можно реализовать с использованием встроенной функции 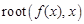 . С помощью этой функции, методом секущих, определяется корень уравнения
. С помощью этой функции, методом секущих, определяется корень уравнения 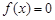 . Перед обращением к функции следует записать левую часть функции
. Перед обращением к функции следует записать левую часть функции  в виде функции пользователя и задать начальное приближение корня.
в виде функции пользователя и задать начальное приближение корня.
Встроенная функция 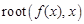 выдает значение переменной
выдает значение переменной  , при которой
, при которой  не превышает значение системной переменной TOL (точность). По умолчанию TOL = 10-3, поэтому в ряде случаев, чтобы функция
не превышает значение системной переменной TOL (точность). По умолчанию TOL = 10-3, поэтому в ряде случаев, чтобы функция 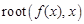 работала правильно, может потребоваться уменьшить значение системной переменной до TOL = 10-7.
работала правильно, может потребоваться уменьшить значение системной переменной до TOL = 10-7.
Моделирование коэффициента летучести реальных газов.
Для учета степени отклонения свойств реальных химически активных газовых систем от идеальных систем введен специальный термодинамический параметр – термодинамическая летучесть (фугитивность), которая обычно обозначается 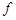 .
.
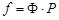 . (61)
. (61)
Летучесть пропорциональна реальному давлению . Коэффициентом пропорциональности
. Коэффициентом пропорциональности 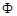 в уравнении (61) называют коэффициент летучести индивидуального вещества. Термодинамическая летучесть, в отличие от термодинамической сжимаемости, измеряется в тех же единицах, что и давление. Фактически летучесть является фиктивным давлением, подстановка которого в уравнение состояния идеального газа превращает это уравнение в уравнение состояния реального газа.
в уравнении (61) называют коэффициент летучести индивидуального вещества. Термодинамическая летучесть, в отличие от термодинамической сжимаемости, измеряется в тех же единицах, что и давление. Фактически летучесть является фиктивным давлением, подстановка которого в уравнение состояния идеального газа превращает это уравнение в уравнение состояния реального газа.
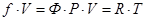 . (62)
. (62)
Поскольку существует понятие парциального давления, то можно говорить и о парциальной летучести. При этом уравнение (61) трансформируется в уравнение:
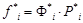 . (63)
. (63)
Тогда под коэффициентом пропорциональности  понимают коэффициент парциальной летучести. Индекс
понимают коэффициент парциальной летучести. Индекс  является индексом компонента, а индекс «٭» указывает на парциальность.
является индексом компонента, а индекс «٭» указывает на парциальность.
 . (64)
. (64)
Очевидно, что коэффициенты летучести веществ являются безразмерными параметрами. Коэффициенты летучести не определяются теоретически. Как и в случае с термодинамической сжимаемостью, коэффициенты летучести рассчитываются по известным косвенным экспериментальным параметрам. В качестве таких параметров используют критические параметры веществ  . Обычно в уравнении (64) при моделировании за парциальные коэффициенты летучести ингредиентов химически активной газовой смеси принимают коэффициенты летучести индивидуальных веществ.
. Обычно в уравнении (64) при моделировании за парциальные коэффициенты летучести ингредиентов химически активной газовой смеси принимают коэффициенты летучести индивидуальных веществ.
Если воспользоваться моделью состояния Редлих-Квонга [см. уравнения (54)–(56)], то математическая модель коэффициента летучести примет вид:
 , (65)
, (65)
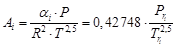 , (66)
, (66)
 , (67)
, (67)
 , (68)
, (68)
 . (69)
. (69)
Если выразить в соответствии с уравнениями (55)–(56) экспериментальные константы 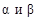 для i-го вещества через его индивидуальные опытные критические свойства
для i-го вещества через его индивидуальные опытные критические свойства  , то система уравнений (65)–(69) для моделирования коэффициента летучести примет вид:
, то система уравнений (65)–(69) для моделирования коэффициента летучести примет вид:
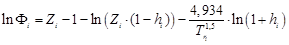 , (70)
, (70)
 , (71)
, (71)
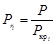 , (72)
, (72)
 , (73)
, (73)
 . (74)
. (74)
Из анализа математической модели следует, что коэффициент летучести чистого вещества есть функция от трех параметров:
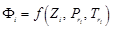 . (75)
. (75)
Моделирование равновесного состава идеальной газовой системы.
Моделирование термодинамики химического превращения включает в себя прогнозирование равновесного состава реакционной газовой смеси и степени превращения целевого компонента при заданных параметрах технологического процесса 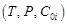 . Равновесный состав для газовой системы, выраженной стехиометрическим уравнением (1), определяется из известного отношения для константы химического равновесия:
. Равновесный состав для газовой системы, выраженной стехиометрическим уравнением (1), определяется из известного отношения для константы химического равновесия:
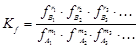 . (76)
. (76)
Парциальные летучести исходных и конечных веществ  и
и 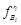 пропорциональны парциальному давлению
пропорциональны парциальному давлению  . Если воспользоваться моделью Дальтона, то абстрактное парциальное давление выразится через реальное давление в системе и мольную концентрацию соответствующего ингредиента газовой смеси.
. Если воспользоваться моделью Дальтона, то абстрактное парциальное давление выразится через реальное давление в системе и мольную концентрацию соответствующего ингредиента газовой смеси.
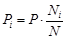 . (77)
. (77)
В итоге уравнение (76) примет вид
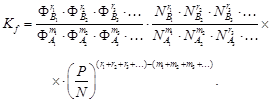 (78)
(78)
Или в более краткой форме:
 , (79)
, (79)
где  – соответственно индексы начальных и конечных веществ;
– соответственно индексы начальных и конечных веществ; 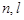 – соответственно число начальных и конечных веществ.
– соответственно число начальных и конечных веществ.
Уравнение (79) можно декомпозировать на две составляющие и представить в виде
 . (80)
. (80)
Первый множитель в уравнении (80) характеризует отклонение свойств изучаемой реальной газовой системы от идеальной и представляет собой коэффициент летучести газовой смеси.
 . (81)
. (81)
Второй множитель является константой равновесия идеальной газовой системы.
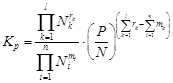 . (82)
. (82)
Для моделирования количества молей реагирующих газов следует воспользоваться разработанной ранее формализованной моделью стехиометрического реактора.
Константа химического равновесия выражается из уравнения (50) и представляется в виде
 , (83)
, (83)
Уравнение (83) необходимо дополнить математической моделью изменения потенциала Гиббса.
Для расчета равновесного состава необходимо произвести «сшивку» уравнений (80) и (83), в которых правые части представляют собой сложные функции от всего комплекса величин, выбранных в качестве определяющих параметров моделируемой газовой системы.
Для моделирования коэффициента летучести газовой смеси  , входящего в уравнение (80), используется соответствующая модель.
, входящего в уравнение (80), используется соответствующая модель.
– Конец работы –
Эта тема принадлежит разделу:
Гартман Т. Н., Клушин Д. В. Основы компьютерного моделирования химико-технологических процессов
На сайте allrefs.net читайте: 1. Гартман Т. Н., Клушин Д. В. Основы компьютерного моделирования химико-технологических процессов. – М.: ИКЦ «Академкнига», 2006. – 416 с....
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Поиск экстремума функции средствами MathCad
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов