Принцип дискриминации и сравнительных суждений
После иерархического или сетевого воспроизведения проблемы следует этап установления приоритетов критериев и оценки каждой из альтернатив по критериям с целью выявления самой важной из них.
ПАРНЫЕ СРАВНЕНИЯ. В МАИ элементы задачи сравниваются попарно по отношению к их воздействию (“весу” или “интенсивности”) на общую для них характеристику. Результаты парных сравнений обычно представляют в виде матрицы.
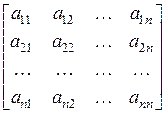 ,
,
где 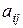 – числовое выражение оношения веса элемента i к весу элемента j. Поэтому должно выполняться условие антисимметричности
– числовое выражение оношения веса элемента i к весу элемента j. Поэтому должно выполняться условие антисимметричности 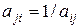 .
.
Пусть А1, А2, ..., Аn – множество сравниваемых элементов между собой, а w1, w2, ..., wn – их веса, причем 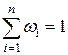 . Тогда идеальная матрица парных сравнений (МПС) принимает вид:
. Тогда идеальная матрица парных сравнений (МПС) принимает вид:
| А1 | А2 | ... | Аn | ||
| А1 | w1/w1 | w1/w2 | ... | w1/wn | |
| А2 | w2/w1 | ... | w2/wn | = А | |
| ... | ... | ... | ... | ||
| Аn | wn/w1 | wn/w2 | ... |
Идеальная МПС: 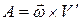 ,
,
где  – элементы матрицы A;
– элементы матрицы A;
 – вектор весов;
– вектор весов;
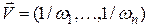 – транспонированный вектор.
– транспонированный вектор.
Получить численные значения относительной важности элементов задачи можно тогда, когда возможны количественные изменения. Например, когда рассматривается отношение веса камней и так далее. В частности можно было бы сравнить геометрические размеры домов. Однако оценка только геометрических размеров не всегда приемлема, так как, вообще говоря, важна планировка комнат и так далее.
Имеется сфера социальных, политических, эмоциональных и других исследований, где количественные сравнения, как правило, невозможны. Поэтому используются качественные суждения.
В МАИ для проведения субъективных парных сравнений разработана шкала экспертных суждений. Каждое из приведенных суждений кодируется числом. В МАИ для кодирования используется номер по порядку строк таблицы.
| Шкала | |
| Равная важность | |
| Умеренное превосходство | |
| Существенное превосходство | |
| Значительное превосходство | |
| Очень сильное превосходство | |
| 2, 4, 6, 8 | Промежуточные решения |
Например, если придано умеренное превосходство элемента  над элементом
над элементом 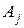 , то полагают
, то полагают 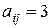 , где
, где 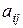 – значение элемента МПС на пересечении строки с номером i и столбца с номером j. Тогда должно быть
– значение элемента МПС на пересечении строки с номером i и столбца с номером j. Тогда должно быть  . В противном случае, когда наоборот элемент
. В противном случае, когда наоборот элемент 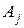 по мнению экспертов умеренно превосходит
по мнению экспертов умеренно превосходит  , то
, то 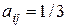 , а
, а 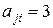 .
.
Если уровень превосходства  над
над 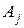 находится по мнению эксперта между умеренным и существенным превосходством, то полагаем
находится по мнению эксперта между умеренным и существенным превосходством, то полагаем  , а
, а 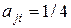 (или наоборот в противном случае).
(или наоборот в противном случае).
Суть обработки заключается в аппроксимации полученной МПС матрицей вида  , то есть
, то есть 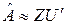 , где
, где 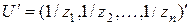 . Главная задача заключается в определении компонент вектора
. Главная задача заключается в определении компонент вектора 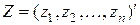 , что позволяет ранжировать элементы А1, А2, ..., Аn, считая полученные значения
, что позволяет ранжировать элементы А1, А2, ..., Аn, считая полученные значения  их весами. Отметим, что по смыслу всегда должны выполняться неравенства
их весами. Отметим, что по смыслу всегда должны выполняться неравенства  .
.
Компоненты искомого вектора весов, с помощью которого аппроксимируется МПС, равны среднему геометрическому, то есть корню n-й степени из произведения элементов соответствующей строки аппрксимирующей матрицы
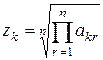 .
.
Тогда  (
( и
и 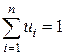 ).
).
Отметим, что если выполняется условие “идеальности” элементов матрицы, то действительно имеет место соотношение 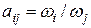 .
.
Весьма полезным является индекс согласованности (ИС), который дает информацию о степени нарушения численной (кардинальной 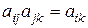 ) и транзитивной (порядковой) согласованности. Для улучшения согласованности рекомендуется поиск дополнительной информации и пересмотр данных. Отсутствие согласованности может быть серьезным ограничивающим фактором для исследования некоторых проблем.
) и транзитивной (порядковой) согласованности. Для улучшения согласованности рекомендуется поиск дополнительной информации и пересмотр данных. Отсутствие согласованности может быть серьезным ограничивающим фактором для исследования некоторых проблем.
Вместе с МПС мы имеем меру оценки степени отклонения от согласованности. Когда такие отклонения превышают установленные пределы, следует перепроверить суждения в матрице.
Индекс согласованности (ИС) в каждой матрице и для всей иерархии может быть приближенно получен вычислением вручную:
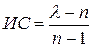 ,
,
где  (для обрабатываемой матрицы всегда
(для обрабатываемой матрицы всегда  );
);
 ;
;
n – число сравниваемых элементов.
Теперь сравнивая эту величину с той, которая получилась при случайном выборе количественных суждений из шкалы 1/9, 1/8, 1/7, …, 1, 2, …, 9 и образовании обратно симметричной матрицы. Ниже приведены средние согласованности (СС) для случайных матриц разного порядка.
| Размер матрицы | ||||||||||
| СС | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
Если разделить ИС на число, соответствующее СС матрицы того же порядка, получим отношение согласованности (ОС): ОС = ИС / ССn. Величина ОС должна быть порядка 10% или меньше, чтобы быть приемлемой. В некоторых случаях можно допустить 20%, но не более (например, в случае размерности матрицы 5х5 и выше). Если ОС выходит из этих пределов, то ЛПР нужно пересмотреть задачу, дополнительно ее исследовать и проверить свои суждения.