Дифференциальные уравнения

Некоторые понятия теории дифференциальных уравнений.

Многие процессы экономики, физики, химии, астрономии, биологии описываются одной функцией у=у(х), заданной на некотором множестве Х или несколькими функциями. Эти функции могут изменяться во времени.

Рассмотрим некоторые процессы, математические характеристики которых приводят к дифференциальным уравнениям.

Задача 1

Определить кривую, проходящую через точку (1;1) такую, что угловой коэффициент касательной в каждой её точке равен удвоенной ординате точке касания.

Пусть искомая кривая является графиком функции у=у(х). Существование касательной в каждой точке кривой означает существование производной 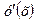в каждой точке х области определения функции у=у(х) .Тогда тангенс угла наклона касательной к рассматриваемой кривой в точке с координатами (х;у) равен 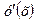и по условию задачи, он же равен 2у(х).Таким образом, получаем следующее соотношение , связывающее искомую функцию и её производную.

Все функции, удовлетворяющие данному уравнению, имеют вид .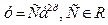

То, что эти функции удовлетворяют полученному уравнению, проверяется непосредственной подстановкой.

Из всей совокупности кривых, задаваемых формулой 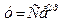выберем ту, что проходит через точку (1;1) :

.

Поэтому уравнение искомой кривой имеет вид: .

Определение.

Пусть некоторый процесс описывается функцией у=у(х), заданной и n>1 раз дифференцируемой на некотором множестве Х; эта функция неизвестна, но известна функциональная зависимость между независимой переменной х, 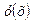и её производными 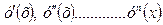до n-го порядка. Тогда уравнение 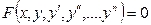(1)называется дифференциальным уравнением n-го порядка.

Порядок наивысшей производной (или дифференциала), входящей в дифференциальное уравнение, называется его порядком.

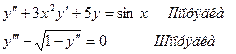
Определение.

Любая функция, удовлетворяющая дифференциальному уравнению (1) называется решением или интегралом этого уравнения.

Определение.

Решение дифференциального уравнения, если оно существует, число произвольных постоянных которого равно порядку уравнения, называется общим решением данного дифференциального уравнения.

Определение.

Решение дифференциального уравнения при определенных значениях произвольных постоянных называется частным решением этого дифференциального уравнения.