рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Компьютеры
- /
- Дифференциальные уравнения I порядка
Реферат Курсовая Конспект
Дифференциальные уравнения I порядка
Дифференциальные уравнения I порядка - раздел Компьютеры, Непрерывность функции. Точки разрыва. Асимптоты графика функции Простейшим Дифференциальным Уравнением I Порядка Называется Д...
Простейшим дифференциальным уравнением I порядка называется дифференциальное уравнение вида 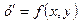 (2) , где f(x) – функция, определенная и непрерывная на некотором множестве Х
(2) , где f(x) – функция, определенная и непрерывная на некотором множестве Х 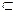 R
R
Общее решение уравнения (2) может быть записано в виде 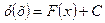 , где F(x) - одна из первообразных функции f(x), С – произвольное действительное число.
, где F(x) - одна из первообразных функции f(x), С – произвольное действительное число.
Пример 1.
Запишите общее решение дифференциального уравнения
Одна из первообразных функции 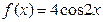 будет
будет 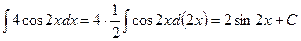 .
.
Таким образом, общее решение данного дифференциального уравнения 
Пример 2.
Найдите решение следующей задачи
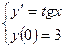
Функция 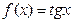 определена на каждом из промежутков
определена на каждом из промежутков 
Одной из первообразных функции 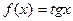 будет
будет 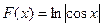 область определения которой совпадает с указанным выше интервалом.
область определения которой совпадает с указанным выше интервалом.
Тогда общее решение имеет вид 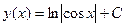 . Подберем значение С так, чтобы получить решение задачи
. Подберем значение С так, чтобы получить решение задачи 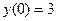 . Подставляя
. Подставляя 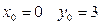 в общее решение, получаем
в общее решение, получаем 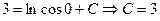 . Итак, решением рассматриваемой задачи будет функция
. Итак, решением рассматриваемой задачи будет функция  .
.
Представив производную 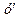 в виде отношения дифференциалов
в виде отношения дифференциалов 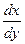 , уравнение (2) можно записать в так называемой дифференциальной форме:
, уравнение (2) можно записать в так называемой дифференциальной форме:
 , где
, где 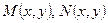 - некоторые функции переменных х и у.
- некоторые функции переменных х и у.
Если функция 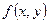 такова, что её можно представить в виде произведения двух функций, из которых одна является функцией переменной х , а другая – переменной у, то уравнение (2) можно записать в виде:
такова, что её можно представить в виде произведения двух функций, из которых одна является функцией переменной х , а другая – переменной у, то уравнение (2) можно записать в виде:
 (3)
(3)
В таком случае уравнение называют дифференциальным уравнением с разделяющимися переменными.
Например, уравнение 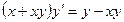 можно записать в виде (3)
можно записать в виде (3)
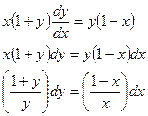
Уравнение  нельзя представить таким образом.
нельзя представить таким образом.
Итак, уравнение с разделяющимися переменными - 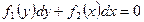 .
.
Общее решение получают в виде:  (4)
(4)
.
Пример
а) 
б) 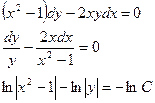
Определение.
Линейным дифференциальным уравнением I порядка называется уравнение вида 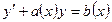 (5)
(5)
где 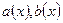 - функции, определенные и непрерывные на
- функции, определенные и непрерывные на 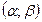
Если 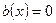 на
на , то уравнение (5) называется однородным:
, то уравнение (5) называется однородным: 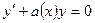
Однородное дифференциальное уравнение I порядка относится к типу уравнений с разделяющимися переменными.
Полагая, что 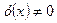 и разделив последнее уравнение, получим
и разделив последнее уравнение, получим 
Из него находим, что

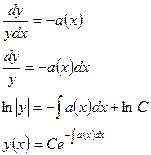
Итак,  - это и есть общее решение однородного дифференциального уравнения I порядка.
- это и есть общее решение однородного дифференциального уравнения I порядка.
Пример.
Постройте общее решение уравнения 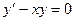
Уравнение является линейным однородным дифференциальным уравнением I порядка.
В рассматриваемом примере 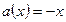 , значит
, значит 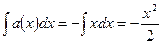 ,
,
Подставим найденный интеграл в формулу общего решения 
Теорема.
Пусть 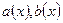 - функции, определенные и непрерывные на
- функции, определенные и непрерывные на 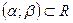 . Тогда общее решение уравнения (5) имеет вид
. Тогда общее решение уравнения (5) имеет вид 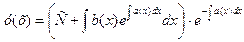 (6)
(6)
Это утверждение проверяется непосредственной подстановкой.
Пример.
Постройте общее решение уравнения 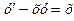
Это дифференциальное неоднородное уравнение I порядка, поэтому общее решение будем искать по формуле (6). 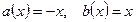
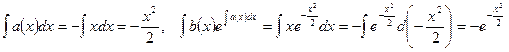 , значит
, значит
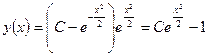 - общее решение искомого уравнения.
- общее решение искомого уравнения.
– Конец работы –
Эта тема принадлежит разделу:
Непрерывность функции. Точки разрыва. Асимптоты графика функции
Правила дифференцирования... Таблица производных основных функций...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Дифференциальные уравнения I порядка
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов