Теорема 2. Для того чтобы функция являлась решением уравнения (2), необходимо и достаточно, чтобы число являлось корнем уравнения

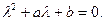(4)

 

Доказательство. Очевидно, что для указанной функции 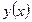будем иметь 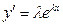и 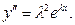Но тогда условие «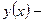решение уравнения (2)» эквивалентно условию «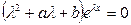», а это последнее- уравнению (4).

Теорема доказана.

Примечание. Уравнение (4) носит название характеристического уравнения для дифференциального уравнения (2).

 

Рассмотрим различные случаи разрешимости уравнения (4).

Случай 1. Дискриминант уравнения (4) положителен.

В этом случае уравнение (4) имеет два действительных различных корня, которые мы обозначаем 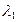и 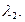Каждый из этих корней порождает соответствующее решение 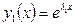и 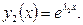Очевидно, что отношение функций 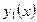и отлично от постоянной величины, и поэтому общее решение линейного однородного дифференциального уравнения (2) будет иметь вид:

 

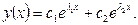
Случай 2. Дискриминант уравнения (4) равен нулю.

Условие равенства нулю дискриминанта уравнения (4) эквивалентно условию 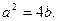В этом случае уравнение (4) имеет два совпадающих корня: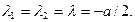

Эти корни порождают одно частное решение 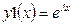уравнения (2), и для построения общего решения уравнения (2) нам необходимо еще одно решение.

Покажем, что в рассматриваемом случае еще одним решением уравнения (2) будет функция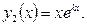

Действительно,

 

Подставляя эти выражения в уравнение (2), получим

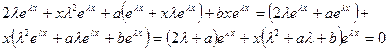
(здесь учтено, что ).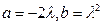

Очевидно, что и в этом случае отношение функций 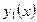и отлично от постоянной, и поэтому общее решение уравнения (2) будет иметь вид:

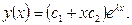(6)

 

Третий случай- случай, когда дискриминант уравнения (3) будет отрицательным, будет рассмотрен нами позже.

Пример 1. Построим общее решение уравнения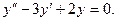

Решение. Характеристическое уравнение (4) для дифференциального уравнения 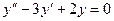будет иметь вид: 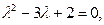а его корнями будут числа и Это означает, что мы имеем случай 1 (случай положительного дискриминанта уравнения (4)), и общее решение рассматриваемого уравнения в соответствии с формулой (5) будет иметь вид:

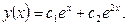
Пример 2. Построим общее решение уравнения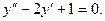

Решение. Для данного дифференциального уравнения характеристическое уравнение (4) будет иметь вид: 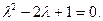Дискриминант этого уравнения равен нулю, и мы имеем случай 2. Корнями характеристического уравнения (4) будут 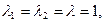а общее решение, в соответствии с формулой (6), имеет вид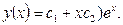

Перейдем теперь к рассмотрению линейного неоднородного дифференциального уравнения второго порядка(1).

Принципиальное значение в проблеме построения его общего решения имеет следующая теорема.

Теорема 3. Общее решение неоднородного дифференциального уравнения (1) имеет вид:

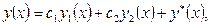(7)