Эластичность функции

 

Будем рассматривать дифференцируемую функцию 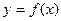. Как и ранее, 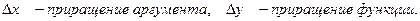Отношения 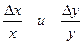представляют собой относительные приращения аргумента и функции соответственно.

Величина 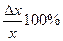показывает, сколько процентов составляет приращение ∆х относительно величины самой переменной х. Аналогичную характеристику дает и величина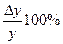

Отношение 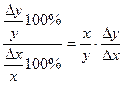показывает, сколько процентов составит среднее ( на промежутке от х до х+∆х) относительное приращение функции, если относительное приращение аргумента составляет 1%.

Предел 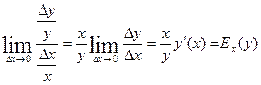называют эластичностью функции по её аргументу в точке х (читают: «Эластичность игрек относительно икс»).Эластичность функции по её аргументу показывает, на сколько процентов изменится значение функции при увеличении аргумента в точке х на 1%.

Таким образом, эластичность у по её аргументу х можно вычислить по формуле

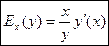
Пример1

Рассчитайте эластичность функции 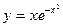при х = 1

1.

2.

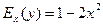
3. х = 1,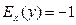

Это означает, что при увеличении х на 1% у уменьшится на 1%

При х = 2, 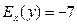, т.е. при увеличении х на 1% у уменьшится на 7%

 

Пример2

Известно, что спрос на товар зависит от доходов потребителей. При увеличении доходов потребители могут переключится на товар лучшего качества или на какой-либо заменитель товара. Таким образом, спрос q зависит от дохода r, q=q(r). Эластичность спроса относительно дохода показывает, на сколько процентов увеличится спрос при увеличении дохода на 1%.

Например, если q(r)=50-0,1r, то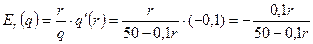

Так, при доходе r =10 получаем , 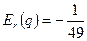, а при увеличении дохода на 10% спрос уменьшится на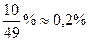

 

Замечание1

Спрос q на товар зависит от цены р, q=q(p) , причем обычно спрос понижается при увеличении цены и тогда . Поэтому эластичностью спроса q относительно цены р называют величину . Она показывает, на сколько процентов уменьшится спрос при увеличении цены на 1%.

 

Замечание1

Спрос называют эластичным, есл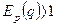и . При 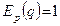спрос называют нейтральным. Если 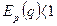, то говорят, что спрос неэластичен.

Для функции спроса q (p)=20-3p найдем эластичность спроса по цене при р=2.

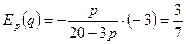
Можно сделать вывод, что при повышении первоначальной цены на 1% спрос уменьшиться на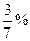

Пример3

Зависимость спроса q и предложения s от цены р задается функциями 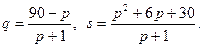Выясним, что произойдет в условиях равновесия рынка при увеличении цены на 1%.

Условия равновесия означают, что спрос и предложения уравновешены, q (p)=s(p), т.е. 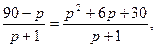откуда р=5. Эластичность спроса по цене При р=5 получаем . Следовательно, при увеличении цены на 1% СПРОС УМЕНЬШИТСЯ ПРИБЛИЗИТЕЛЬНО НА 0,89%

Эластичность предложения по цене 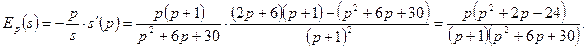При р=5 получаем 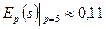. Значит, при увеличении цены на 1% предложение увеличится приблизительно на 0,11%.

*Для функции спроса 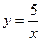в зависимости от цены х найти эластичность спроса по цене в точках х=1, х=4, х=8, х=10.

*Для функции предложения у=8х+3 в зависимости от цены х найти эластичность предложения по цене в каждой из точек х=2, х=3, х=5, х=10.

* В предложенных выше заданиях выяснить, является ли спрос или предложение эластичным, нейтральным или неэластичным в каждом из рассмотренных случаев.