рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Компьютеры
- /
- Применение производной к исследованию функции
Реферат Курсовая Конспект
Применение производной к исследованию функции
Применение производной к исследованию функции - раздел Компьютеры, Непрерывность функции. Точки разрыва. Асимптоты графика функции Функция Y=F(X) Называется Возрастающей...
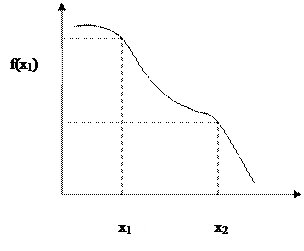
Функция y=f(x) называется возрастающей в промежутке 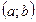 , если для любых
, если для любых 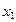 и
и 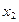 , принадлежащих этому промежутку и таких , что
, принадлежащих этому промежутку и таких , что 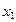 <
< 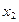 , имеет место неравенство
, имеет место неравенство 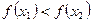 .
.
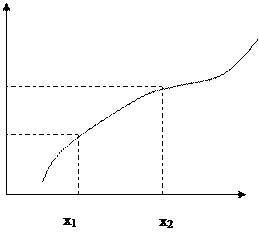 |
f(х2)
f(х1)
Функция y=f(x) называется убывающей в промежутке 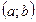 , если для любых
, если для любых 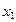 и
и 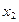 , принадлежащих этому промежутку и таких , что
, принадлежащих этому промежутку и таких , что 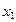 <
< 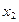 , имеет место неравенство
, имеет место неравенство 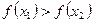 .
.
 |
f(x2)
Как возрастающие, так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает, - промежутками монотонности.
Возрастание и убывание функции y=f(x) характеризуется знаком её производной.
Теорема
Для того чтобы дифференцируемая на 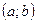 функция y=f(x) не убывала (не возрастала) на этом интервале, необходимо и достаточно чтобы
функция y=f(x) не убывала (не возрастала) на этом интервале, необходимо и достаточно чтобы 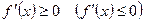 для всех х из этого интервала.
для всех х из этого интервала.
Если же для любого х из 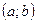
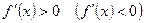 то функция y=f(x) монотонно возрастает (монотонно убывает) на этом интервале.
то функция y=f(x) монотонно возрастает (монотонно убывает) на этом интервале.
Из теоремы следует, что для того чтобы функция y=f(x) была постоянной на 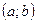 , необходимо и достаточно, чтобы выполнялось условие:
, необходимо и достаточно, чтобы выполнялось условие: 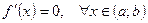
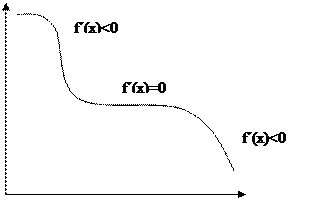
Внутренние точки области определения, в которых производная не существует или равна нулю, называются критическими.
Точка 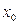 из области определения D(f) точкой максимума (минимума) этой функции, если существует такой интервал
из области определения D(f) точкой максимума (минимума) этой функции, если существует такой интервал 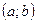 ,
,  , не выходящий из области определения D(f), что для всех х ≠
, не выходящий из области определения D(f), что для всех х ≠ 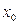 , выполняется неравенство
, выполняется неравенство 
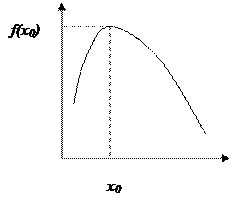 | 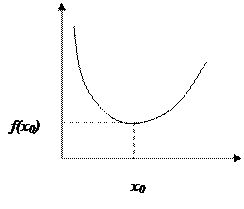 |
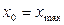
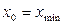
Точки максимума и минимума функции называются точками экстремума, а значения функции в этих точках – экстремумы функции.
Следующая теорема показывает, что точки экстремума следует искать среди критических точек функции.
Теорема Ферма
Если точка 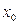 - точка экстремума функции y=f(x) и в этой точке существует производная, то
- точка экстремума функции y=f(x) и в этой точке существует производная, то 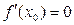
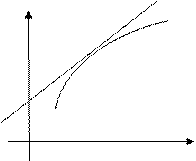
Свойство выпуклости (вогнутости) функции как и монотонности интуитивно понятно из геометрических представлений о графике функции:
 | |||
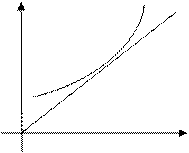 | |||
а) б)
График а) естественно назвать выпуклым вверх, а график б) - выпуклым вниз.
Введем понятие выпуклости для дифференцируемых функций на интервале в каждой точке графика функции, в которой можно провести касательную.
Определение. Дифференцируемая на интервале (а;b) функция f(x) называется выпуклой вверх (вниз), если для любого 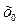 и х из этого промежутка справедливо неравенство:
и х из этого промежутка справедливо неравенство: 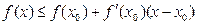 (
(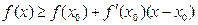 )
)
Т.е. дифференцируемая функция выпуклая вверх (вниз) на (а;b) если все точки графика функции лежат не выше (не ниже) касательной, проведенной к графику функции в любой точке из (а;b).
Теорема(достаточное условие выпуклости функции)
Пусть функция у=f(x) определена и дважды дифференцируема на (а;b), существует 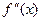 тогда если
тогда если 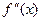 >0 на (а;b), то на этом промежутке функция выпуклая вниз (вогнутая), если
>0 на (а;b), то на этом промежутке функция выпуклая вниз (вогнутая), если 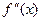 <0, то на этом промежутке функция выпуклая вверх (выпуклая).
<0, то на этом промежутке функция выпуклая вверх (выпуклая).
Определение. Точка 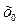 из D(f) функции f(x) называется точкой перегиба, если:
из D(f) функции f(x) называется точкой перегиба, если:
1.в этой точке функция непрерывна;
2.существует интервал (а;b),  такой, что на интервалах
такой, что на интервалах 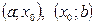 направления выпуклости противоположны, т.е. в точке
направления выпуклости противоположны, т.е. в точке 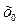 выпуклость сменяется вогнутостью или наоборот.
выпуклость сменяется вогнутостью или наоборот.
 |
Теорема. (необходимое условие точки перегиба)
Пусть дана функция у=f(x) дважды дифференцируемая на (а;b). Если в точке  график имеет перегиб и существует конечная вторая производная
график имеет перегиб и существует конечная вторая производная 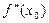 , то
, то 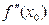 =0.
=0.
Теперь можно указать схему исследования функции на выпуклость (вогнутость):
1. Устанавливаем D(f)
2. Находим вторую производную
3. Определяем точки разрыва второй производной и из уравнения 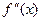 =0 – нули второй производной
=0 – нули второй производной
4. Найденными точками разбиваем D(f) на интервалы, в каждом из которых определяем знак второй производной. Строим кривую знаков.
5. По кривой делаем вывод о выпуклости (вогнутости) функции и наличии точек перегиба.
Пример.
Исследовать на выпуклость функции а)  , б)
, б) 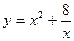
а) Область определения данной функции D(f)=R
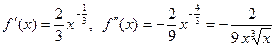
Нулей 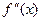 не имеет . Точкой разрыва является точка
не имеет . Точкой разрыва является точка 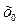 =0
=0
- -

На интервалах (- ;0) и (0;
;0) и (0; )функция выпуклая вверх. Точек перегиба нет.
)функция выпуклая вверх. Точек перегиба нет.
б) D(y)=R {0}
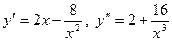
Точка разрыва второй производной 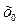 =0, нули второй производной найдем из уравнения
=0, нули второй производной найдем из уравнения 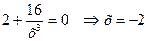
+ - +
 | |||||||||||||
| |||||||||||||
| | |||||||||||||
 | |||||||||||||
 |  | ||||||||||||
| |
На (- ;-2) и (0;
;-2) и (0; ) функция выпуклая вниз (вогнутая), на (-2;0)- выпуклая вверх (выпуклая),
) функция выпуклая вниз (вогнутая), на (-2;0)- выпуклая вверх (выпуклая), 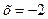 точка перегиба.
точка перегиба.
Наиболее полное исследование функции и построение её графика можно провести по следующей схеме:
1. Найти область определения функции.
2. Четность, периодичность.
3. Исследовать функцию на непрерывность: наличие точек разрыва, их характеристика; асимптоты графика.
4. Найти точки пересечения графика с осями координат.
5. Определить критические точки, промежутки возрастания и убывания функции, а также экстремумы функции.
6. Найти интервалы выпуклости и вогнутости, точки перегиба.
7. Построение графика.

Пример.
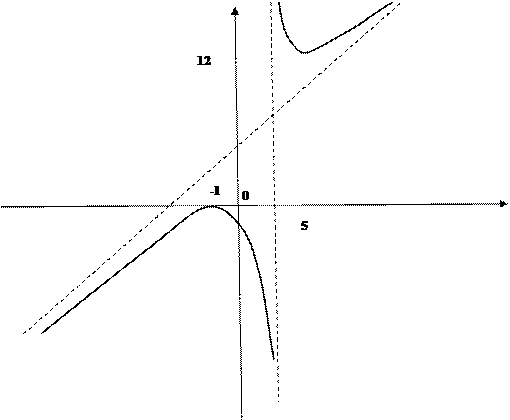
Построить график функции 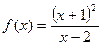
1.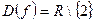
2.Функция не является ни чётной ни нечётной; кроме того, она не является периодической.
3.Функция непрерывна в области определения.
х=2 – точка разрыва
Исследуем функцию в окрестности точки х=2

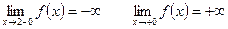
Следовательно, х=2 – вертикальная асимптота
Найдем наклонные: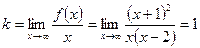
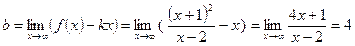
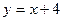 является наклонной асимптотой графика функции.
является наклонной асимптотой графика функции.
4. (0;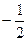 ), (-1;0) – точки пересечения с координатными осями.
), (-1;0) – точки пересечения с координатными осями.
5. 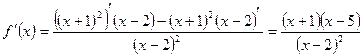
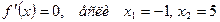 - критические точки.
- критические точки.
+ - - +

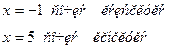
Найдем экстремумы функции:
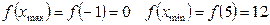
6.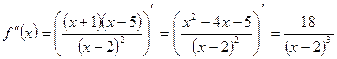
Вторая производная в нуль не обращается на всей области определения функции.
- +
 | |||
 |
– Конец работы –
Эта тема принадлежит разделу:
Непрерывность функции. Точки разрыва. Асимптоты графика функции
Правила дифференцирования... Таблица производных основных функций...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Применение производной к исследованию функции
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов