Интегральное исчисление. Неопределенный интеграл и его свойства

Будем считать, что мы достаточно хорошо освоили операцию дифференцирования одной переменной и, используя таблицу производных и основные правила дифференцирования, уверенно вычисляем производные основных элементарных функций и различных алгебраических выражений, содержащих эти функции. Так, например, 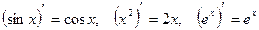и т.п., каждый раз по заданной функции F(x) находим её производнуюf(x) то есть 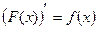. Вполне естественно поставить обратную задачу: по заданной производной f(x) , некоторой функции восстановить саму функцию F(x). Например, если 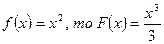, что легко проверяется дифференцированием.

 

Определение

Пусть функции f(x) и F(x) определены на (a;b). Если функция F(x) имеет производную на (a;b) и для всех х из этого интервала выполняется равенство 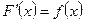(1), то функция F(x) называется первообразной для функции f(x) на интервале (a;b).

Теорема

Если определенная на интервале (a;b) функция f(x) имеет на нем хотя бы одну первообразную F(x), то она имеет на этом интервале бесконечное множество первообразных, элементами которого являются функции F(x)+С, 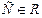и только они.

Пример.

Каждая из функций 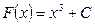, где С – произвольное действительное число, является первообразной для функции 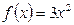на R.

Из теоремы очевидно, что при любом действительном С график функции F(x)+С получается из графика функции F(x) путем параллельного переноса последнего на величину С вдоль оси ординат.

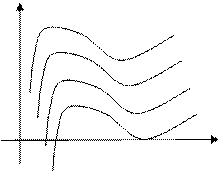
Таким образом, теорема утверждает, что вся

совокупность графиков первообразных функции f(x)

получается из одного из них путем всевозможных

параллельных переносов этого графика вдоль оси

ординат.

 

 

Определение.

Совокупность всех первообразных функций для функции f(x) на интервале (a;b) называется неопределенным интегралом от функции f(x) на этом интервале.

Обозначается: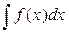

Функция f(x) называется подынтегральной, знак называется знаком интеграла, а выражение , записываемое справа от него: f(x)dx – подынтегральным выражением.

Нахождение неопределенного интеграла от функции f(x), заданной на некотором интервале 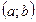, называется интегрированием.

 

В соответствии с определением и теоремой выше, можно записать: 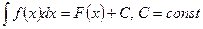(2)

Если первообразная (а значит, и неопределенный интеграл) для функции f(x) на интервале (a;b) существует, то подынтегральное выражение представляет собой дифференциал любой из этих первообразных.

Пусть F(x) – некоторая первообразная на (a;b) , т.е. для любого х из (a;b) выполняется 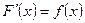, тогда 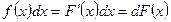(3)

Функция 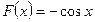одна из первообразных для функции 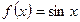на всей числовой прямой, т.е.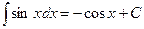

Функция 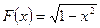является одной из первообразных для функции 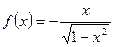на (-1;1), значит 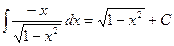на (-1;1)