Кинетика приближения термодинамической системы к конечному состоянию.

Сначала ограничимся случаем, когда выполняется уравнение (23), т.е. система находится вблизи от стационарного состояния. Решая это уравнение, получаем

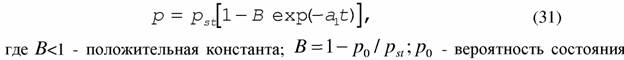
системы в начальный момент времени ί=0. Подставляя (30) и (31) в (24) и учитывая разбиение (16), имеем

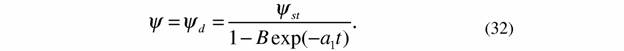
Во время развития и роста организм приближается к конечному стационарному состоянию и с определенного момента он попадает в линейную область, где будет справедливо уравнение (32). Так как в линейной области

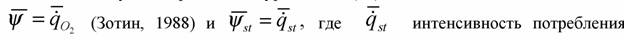
кислорода в конечном стационарном состоянии, то уравнение (32) можно записать в виде, которое поддается экспериментальной проверке:

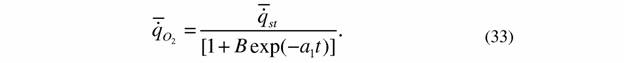
Это уравнение хорошо согласуется с данными, полученными нами для пресноводных двустворчатых моллюсков (рис. 3), и данными Броди (Brody, 1945), полученными для млекопитающих. При определенных допущениях, когда система достаточно близко подходит к конечному стационарному состоянию, уравнение (33) может быть трансформировано следующим образом:

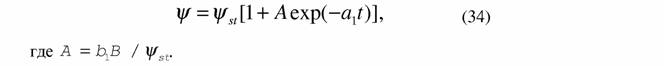
Это уравнение хорошо согласуется с зависимостью, полученной в термодинамике линейных необратимых процессов на основании совершенно иных соображений (см. де Гроот, Мазур, 1964; Зотин, 1988). Уравнение (34) также достаточно хорошо согласуется с экспериментальными данными, полученными для млекопитающих. Так, Броди (Brody, 1945) приводит следующие эмпирические уравнения для описания изменений основного обмена во время роста домашних млекопитающих:

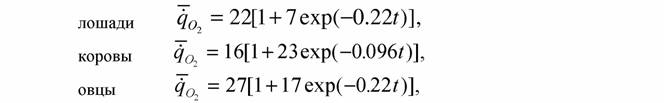
т.е. используют для этих целей уравнение вида (34). В нелинейной области следует использовать разложение (22) в более полном виде. Это сильно усложняет кинетические уравнения. Поэтому, мы ограничились квадратичным выражением (Зотин, Зотина, 1977; Зотина, Зотин, 1980; Зотин, 1988). В этом случае уравнение (25) можно записать в следующем виде

Это уравнение Риккати. Решая его, получим

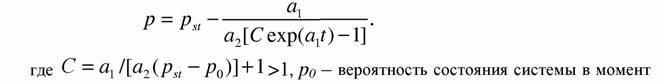
времени t=0. Подставляя это решение в (29), имеем

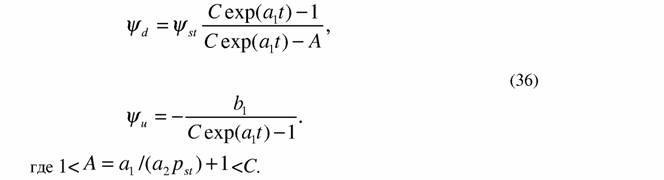
Теперь мы можем использовать полученные соотношения для описания кинетики изменения диссипативных функций во время развития и роста организмов. Анализ уравнений (36) показывает, что Ψ_d положительна на всей области определения, монотонно асимптотически уменьшается, стремясь к Ψ_st . Ψ_u отрицательна на всей области определения монотонно увеличивается, стремясь

реальными данными, полученными при изучении изменения интенсивности потребления кислорода и теплопродукции в оогенезе шпорцевой лягушки, в зародышевом развитии кур, во время роста рыб и насекомых (Зотин, Зотина, 1993) показали, что изменение диссипативных функций может быть описано соотношением (36). Таким образом, опираясь на теорию флуктуации Эйнштейна и некоторые термодинамические соображения, были получены кинетические уравнения для диссипативных функций, которые показывают, что критерии

эволюции отражают процесс перехода системы из менее вероятного в более вероятное состояние.

14. Принцип наискорейшего спуска. Согласно второму началу термодинамики (6) при протекании необратимых процессов энтропия изолированной системы возрастает и к состоянию равновесия достигает максимальной величины. В открытой, неравновесной системе основную роль играет не изменение энтропии, а функция внешней диссипации (13),(18), которая уменьшается при протекании необратимых процессов, и по мере приближения системы к равновесному или стационарному состоянию переходит в диссипативную функцию /см.(16), рис.3/. Эта последняя при протекании необратимых процессов также непрерывно уменьшается (12), а в состоянии равновесия равна нулю (8).

Во всех указанных случаях речь идет о конечной характеристике равновесного состояния (энтропия системы максимальна, диссипативная функция равна нулю). Другими словами, второе начало ничего не говорит о том, как и с какой скоростью осуществляется переходный процесс, а только о его направлении и о конечном значении энтропии или диссипативной функции. Для характеристики самого переходного процесса требуется некий новый принцип, попытка формулировки которого предпринималась многими авторами, опираясь на экстремальные принципы механики и второе начало термодинамики (Циглер, 1966; Преснов, 1973, 19766; 1977; Чернавский, 1975; Шахпаронов, 1987; Swensen,1889; Azzone, 1994; Зотин, Зотин, 1995; Zotin, Zotin, 1996). В конечном счете этот принцип (усиленный критерий эволюции по терминологии Преснова, 1973, 19766) можно сформулировать следующим образом (Зотин, Зотин, 1995):

в процессе приближения термодинамической системы к равновесному или стационарному состояниям функция внешней диссипации убывает наискорейшим возможным способом

Аналитическое выражение для этого критерия имеет вид (см. Преснов, 19766):

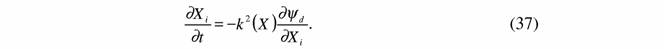
Автономная динамическая система (37) позволяет написать (Преснов, 19766, 1977) для функции внешней диссипации [принимая k²(x) = l]

Циглер (1966), а позднее и другие авторы (Николис, Пригожин, 1979; Swensen, 1989, 1992, 1997; Хазен, 1993, 1996), называет этот принцип законом максимальной скорости порождения энтропии и считает, что его можно вывести из второго начала термодинамики. Записывается этот закон (Swensen, 1989), в обозначениях, принятых в данной работе, в виде неравенства

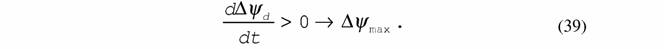
Этот закон можно назвать принципом наикратчайшего спуска (Циглер, 1966) или принципом наискорейшего спуска (Преснов, 19766: Зотин, Зотин, 1995). Шахпаронов (1987) выводит его, как и все законы термодинамики, из принципа наименьшего действия механики. По его представлениям изменение состояния любой физической системы можно характеризовать действием D

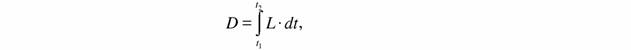
где L - функции Лагранжа, имеющая размерность энергии. Согласно принципу наименьшего действия процесс перехода системы из состояния 1 в состояние 2 протекает так, что функционал D имеет наименьшее из возможных значение. Если задан интервал времени t₂ — t₁ = Const, то при протекании процесса экономится энергия. Если постоянно изменяется L, то экономится время, т.е. процесс протекает наискорейшим путем.

Как считает Чернавский (1975) принцип наименьшего действия механики справедлив только для обратимых процессов, поэтому он применим только для систем близких к равновесию, т.е. в лучшем случае в области термодинамики линейных необратимых процессов. Мы также не думаем, что законы термодинамики можно вывести из принципов механики, хотя попытки такого рода широко известны (Циглер, 1966; Vojta, 1967; Biot, 1970; Дьярматы, 1974; Бахарева, 1976; Garrod, 1984; Шахпаронов, 1987; Хазен, 1993, 1996; Мещереков, Улыбин, 1994) и возможно они в конце концов приведут к успеху.

Если пока оставить в стороне попытки доказательства принципа наискорейшего спуска, опираясь на принципы механики, или второе начало термодинамики, то можно принять принцип наискорейшего спуска в качестве аксиомы или начала термодинамики. Оправданием для такого постулата может служить то, что на его основе легко понять причины появления в процессе приближения больших систем к равновесию подсистем, которые двигаются в обратном направлении, уклоняясь от равновесия. Упоминание о такой возможности имеется в книге Моисеева (1988) и в статье Азоне (Azzone, 1994)*, но

* Оба автора ссылаются при этом на Онзагера (Onsager, 1931a), который первым обосновал такую возможность.

подробнее эта идея разработана в наших работах (Зотин, Зотин, 1995; Zotin, Zotin, 1996), в которых показано, что согласно принципу наискорейшего спуска появление в материнской системе подсистем, уклоняющихся от равновесия, является обязательным событием, так как их движение в направлении неравновесия ускоряет общее движение большой системы к состоянию равновесия.

То, что возникновения подобного рода подсистем ускоряет процесс приближения большой системы к равновесию следует из второго начала термодинамики (Зотин, Зотин, 1995). Действительно, пусть производная псидфункции по времени (38) относится к таким необратимым процессам, среди которых отсутствуют процессы типа (10). Обозначим ее символом R₁. Производная псидфункции по времени для процессов, среди которых присутствуют необратимые процессы типа (10) обозначим через R₂. Для последнего типа процессов мы должны разбить правую часть уравнений (38) на две части

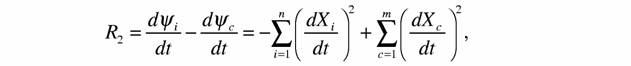
где Ψ_i - функция внешней диссипации уменьшающаяся, a Ψ_c -увеличивающаяся в ходе приближения системы к стационарному или равновесному состоянию. Легко показать, что

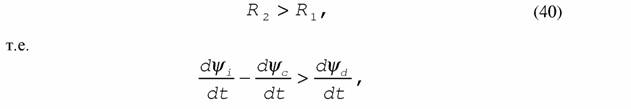
так как согласно второму началу термодинамики для компенсации увеличения псидфункции Ψ_с изменение Ψ_i должно быть больше, чем ∆Ψ_d, т.е. ∆Ψ_i = ∆Ψ_с + ∆Ψ_d. Уклонение подсистемы от равновесия может осуществляться только за счет сопряженных процессов (10), происходящих внутри большой системы. Больше того, согласно второму началу эта компенсация должна

сопровождаться возникновением энтропии, т.е. скорость уменьшения функции внешней диссипации должна в целом возрасти на d∆Ψ_d/dt [см. (39)]. Общая

система будет двигаться к состоянию равновесия более быстрым способом, чем она двигалась бы, если бы уклонения подсистемы в направлении от равновесия не происходило. Другими словами, для осуществления принципа наискорейшего спуска необходимо появление в большой системе подсистем, которые не приближались бы, а уклонялись от равновесного состояния. Условия, ограничения и обязательность появления таких подсистем пока не ясны, но то, что они возможны и желательны следует из принципа наискорейшего спуска и существования сопряженных процессов (10).

75. Кинетика сопряженных процессов. В результате протекания сопряженных процессов происходит уклонение части системы (подсистемы) от

равновесия. Такая подсистема может быть охарактеризована функцией внешней диссипации Ψ_sub большей, чем функция внешней диссипации всей системы Ψ_d.

Логично, поэтому, за меру диссипативной функции сопряженных процессов принять разницу Ψ_c = Ψ_sub - Ψ_d .

Рассмотрим термодинамические силы, влияющие на потоки удельных диссипативных функций всей системы и подсистемы, уклонившейся от равновесия. Уравнение (32) в дифференциальной форме может быть записано следующим образом:

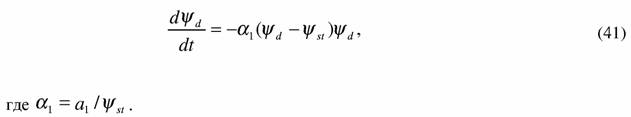
В уравнении (41) левая часть представляет поток функции внешней диссипации, а правая - величину, пропорциональную термодинамической силе. Можно предположить, что сопряженные процессы в системе возникают под действием той же термодинамической силы. С другой стороны, на сопряженные процессы действует также термодинамическая сила, под действием которой подсистема стремится прийти в равновесие со всей системой. Очевидно, по аналогии с уравнением (41) эта сила будет пропорциональна выражению (Ψ_d - Ψ_s_ub)Ψ_Sub. Таким образом, для потока функции внешней диссипации подсистемы можно записать

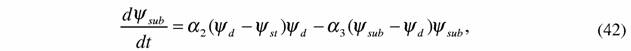
где α₂ и α₃ - коэффициенты пропорциональности. Сопоставление формул (41) и (42) показывает, что кинетика сопряженных процессов будет определяться уравнением

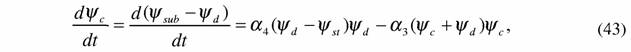
где α₄= α₂+ α₁_. Анализ уравнения (45) показывает, что функция диссипации сопряженных процессов сначала возрастает, достигая максимума, а затем уменьшается, стремясь

В определенных условиях, когда функции внешней диссипации подсистемы и всей системы различаются незначительно, а приближение системы к конечному стационарному состоянию достаточно медленно по сравнению со скоростью

где β - константа. Решением уравнения (44) будет экспонента
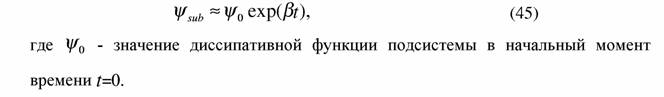