Формирование нижних и верхних оценок целевой функции

 

Прежде чем начать обсуждение данного вопроса, необходимо сказать, что общепринятым является применение метода ветвей и границ для задачи, в которой направление оптимизации приведено к виду минимизации. Для компактности дальнейших обозначений и выкладок запишем задачу дискретного программирования, для которой будем применять метод ветвей и границ, в следующей обобщенной форме:

 

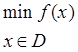(2)

 

где х – вектор оптимизационных переменных, среди которых часть действительных, а часть целочисленных; f(x) – в общем случае нелинейная целевая функция; D – область допустимых решений задачи дискретного программирования общего вида.

Нижние оценки целевой дикции в зависимости от выбранного способа ветвления могут определяться либо для подобластей D_i D либо для подобластей D_i' D' (D_i' и D' получены из соответствующих множеств D_i и D путем снятия условий целочисленности на дискретные переменные).
Нижней оценкой целевой функции f(x) на множестве D_i (или D_i') будем называть величину:

 

(3)

 

Вычисление нижних оценок в каждом конкретном случае может осуществляться с учетом особенностей решаемой задачи. При этом чтобы оценки наиболее эффективно, выполняли свою функцию, они должны быть как можно большими, т.е. быть как можно ближе к действительным значениям min f(x). Это необходимо в первую очередь для того, чтобы нижние оценки как можно точнее отражали действительное соотношение min f(x) на образовавшихся при ветвлении подмножествах и позволяли более точно определять направление дальнейшего поиска оптимального решения исходной задачи.

На рис. 3 показан такой идеальный случай, когда нижние оценки (соединены ломаной штрихпунктирной линией) правильно отражают соотношения между действительными минимальными значениями f(x) (соединены штриховой линией) для четырех подмножеств допустимых решений D₁, D₂, D₃, D₄.

Один из универсальных способов вычисления нижних оценок заключается в решении следующей задачи:

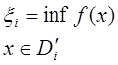(4)

 

Определенная таким образом ξ_i является нижней оценкой f(x) на D_i (или D_i'), так как D_i D_i'.

Если при решении задачи (4) установлено, что 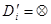, то для общности будем полагать, что .

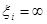Необходимо отметить одно важное свойство нижних оценок, заключающееся в том, что их значения для образовавшихся при ветвлении подмножеств не могут быть меньше нижней оценки целевой функции на множестве, подвергавшемся ветвлению.

Совместно с нижней оценкой в методе ветвей и границ используются верхние оценки f(x). Как правило, вычисляют лишь одно значение верхней оценки 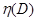, которую определяют как значение целевой функции для лучшего найденного допустимого решения исходной задачи. Такую верхнюю оценку иногда называют рекордом. Если же можно для решаемой задачи достаточно просто и точно получить верхние оценки f(x) для отдельных множеств, образующихся при ветвлении, то их необходимо использовать в методе для уменьшения вычислительной сложности процесса решения. При использовании единой верхней оценки ее первоначальное значение обычно полагают равным бесконечности (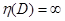), если, конечно, из априорных соображений не известно ни одного допустимого решения исходной задачи. При нахождении первого допустимого решения :

 

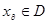(5)

 

Затем при определении более лучшего допустимого решения 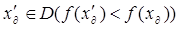верхнюю оценку корректируют:

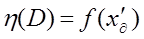(6)

 

Таким образом, значение верхней оценки может лишь уменьшаться в процессе решения задачи.