рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Программирование
- /
- Вид работы: Лекции
- /
- ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Реферат Курсовая Конспект
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ - Лекция, раздел Программирование, Закрепление теоретических знаний, получаемых студентами на лекционных и самостоятельных занятиях по решению задач линейного программирования Вспомним Построение Линейных Зависимостей. Начнём С Уравнений...
Вспомним построение линейных зависимостей. Начнём с уравнений.
 Линейное уравнение с двумя переменными может быть записано a1x1+a2x2 =b. Чтобы построить это уравнение, найдём точки пересечения с осями координат. При х1 = 0 получаем a2x2 =b, откуда х2 = b/a2. При х2 = 0 получаем a1x1 =b, откуда х1 = b/a1 (рис.2.2).
Линейное уравнение с двумя переменными может быть записано a1x1+a2x2 =b. Чтобы построить это уравнение, найдём точки пересечения с осями координат. При х1 = 0 получаем a2x2 =b, откуда х2 = b/a2. При х2 = 0 получаем a1x1 =b, откуда х1 = b/a1 (рис.2.2).
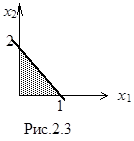 Разделим теперь левую и правую части уравнения на b и перепишем уравнение
Разделим теперь левую и правую части уравнения на b и перепишем уравнение 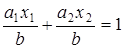 , или
, или 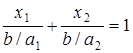 , или
, или  , которое называют уравнением прямой в отрезках. Такое представление уравнения удобно для построения прямой, так как величины a1 и a2 – это отрезки, отсекаемые прямой на тех осях, которые указаны в числителе. Например, 2х1+х2=2 или в форме уравнения в отрезках:
, которое называют уравнением прямой в отрезках. Такое представление уравнения удобно для построения прямой, так как величины a1 и a2 – это отрезки, отсекаемые прямой на тех осях, которые указаны в числителе. Например, 2х1+х2=2 или в форме уравнения в отрезках:  , т.е. a1 =1, a2 =2 (рис.2.3).
, т.е. a1 =1, a2 =2 (рис.2.3).
Теперь вспомним неравенства. Если линейное уравнение с двумя переменных 2х1+х2=2 может быть представлено прямой на плоскости, то неравенство a1x1+ +a2x2 £ b изображается как полуплоскость.
Так неравенство 2х1+х2£ 2 представляет собой заштрихованную полуплоскость, координаты всех точек которой, т.е. х1 и х2 удовлетворяют заданному равенству. Значит, эти значения составляют область допустимых решений (ОДР).
Рассмотрим построение системы линейных неравенств:

или в форме, аналогичной уравнениям в отрезках:

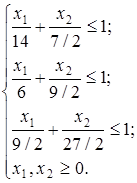
Построим каждое неравенство в системе координат х1б х2 в виде соответствующих полуплоскостей (рис.2.4).
Решение этой системы неравенств – координаты всех точек, принадлежащих ОДР, т.е. АВСДО. Так как в ОДР бесчисленное множество точек, значит рассматриваемая задача имеет бесчисленное множество допустимых решений.
Не любая система линейных неравенств имеет ОДР, т.е. допустимые решения.
Например, построим системы (рис.2.5):
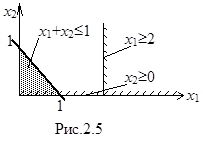

Из рис.2.5 видно, что нет таких точек, которые бы удовлетворяли всем неравенствам системы.
До сих пор рассматривали линейные уравнения и неравенства с двумя переменными. Если перейти к линейным зависимостям с тремя переменными, то тогда они будут описывать плоскость в трёхмерном пространстве; линейное неравенство характеризует полупространства, а система линейных неравенств – многогранник как ОДР в трёхмерном пространстве.
С увеличением числа переменных выше трёх, геометрическая интерпретация невозможна, но система неравенств – ОДР в k-мерном пространстве.
При этом мерность пространства определяют как: если ограничения заданы неравенствами, то k = п, где п – число переменных; если ограничения в виде уравнений, то k = n–т, где т – число уравнений.
Если мы хотим найти оптимальное решение, то должны принять ЦФ. Допустим, мы хотим, чтобы решение было оптимальным в смысле максимизации выпуска в целом. Тогда ЦФ: max L = x1+x2.
Положим L равной какому-либо числу (любому), например 2, и построим уравнение ЦФ: 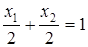 .
.
Так как нам требуется найти оптимальное решение, при котором достигается maxL, будем перемещать линию ЦФ в направлении увеличения L. Очевидно, что оптимальным решением будут координаты точки С, равные  . При этом L = L*.
. При этом L = L*.
Отсюда можно сделать исключительно важный вывод: оптимальное решение – координаты вершины ОДР.
Из этого вывода следует метод решения задач ЛП, который заключается в следующем.
1. Найти вершины ОДР как точки пересечения ограничений.
2. Определить последовательно значения ЦФ в вершинах.
3. Вершина, в которой ЦФ приобретает оптимальное (max или min) значение, является оптимальной вершиной.
4. Координаты оптимальной вершины есть оптимальные значения искомых переменных.
– Конец работы –
Эта тема принадлежит разделу:
Закрепление теоретических знаний, получаемых студентами на лекционных и самостоятельных занятиях по решению задач линейного программирования
На сайте allrefs.net читайте: - закрепление теоретических знаний, получаемых студентами на лекционных и самостоятельных занятиях по решению задач линейного программирования;...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов