Симплексные таблицы

Практические расчеты с использованием симплекс метода – на компьютере. Если вручную, то используются симплекс-таблицы. Будем решать задачу на максимум.

I. После введения добавочных переменных систему уравнений и лин функцию записывают в виде, который называется расширенной системой: (Слайд 2)

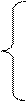а11*Х1 + а12*Х2 + … + а1n*Xn + Xn+1 = В1

а21*Х1 + а22*Х2 + … + а2n*Xn + Xn +2 = В2 …………………………………………………………….

аm1*Х1 + аm2*Х2 + … + аmn*Xn + Xn +m = Вm

F – c1X1 – c2X2 - … - cnXn = 0

Предполагаем, что все добавочные переменные имеют тот же знак, что и свободные члены, в противном случае используется М-метод (рассмотрим дальше).

II. Исходную расширенную систему заносим в первую симплексную таблицу. Последняя строка таблицы, в которой уравнение целевой функции – оценочная. В левом столбце таблицы – основные переменные (базис), в первой строке – все переменные (отмечая при этом основные), во втором столбце – свободные члены. Последний столбец – для оценочных отношений. В рабочую часть таблицы (начиная с третьего столбца и второй строки) занесены коэффициенты Aij.

III. Проверим выполнения критерия оптимальности (при макс – наличие отриц коэффициентов в последней строке, т.к. они с «-»). Если их нет, то достигнут максимум (его значение – в левом нижнем углу таблицы), основные переменные – значение второго столбца, неосновные = 0, т.е. оптимальное БР.

IV. Если критерий оптим не выполнен. То наибольший по модулю отрицательный коэффициент в последней строке определяет разрешающий столбец.

Составляем оценочные отношения каждой строки по правилам:

1) ½Bi/Aij½, если Bi и Aij одного знака и Aij не = 0, Bi не = 0.

2) ¥, если Bi и Aij разного знака и Aij не = 0, Bi не = 0.

3) 0, если Bi = 0 и Aij > 0.

4) ¥, если Bi = 0 и Aij < 0.

5) ¥, если Aij = 0.

Определяем min по I для {½Bi/Aij½}. Если конечного минимума нет, то нет конечного оптимума. Если минимум конечен, то выбирается строка q, на которой он достигается (любая, если их несколько), называется разрешающей строкой. На пересечении разрешающий элемент Aqs.

V. Переходим к следующей таблице по правилам:

1) в левом столбце записываем новый базис: вместо основной переменной Xq – переменную Xs;

2) в столбцах, соответствующих основным переменным, проставляем: 1 – против «своей основной переменной, 0 – против «чужой основной переменной, 0 – в последней строке для всех основных переменных;

3) новую строку с номером q получаем из старой делением на разрешающий элемент Aqs;

4) все остальные новые элементы Aij вычисляем по правилу прямоугольника: (Слайд 3)

 

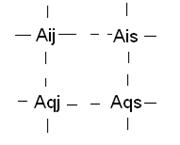
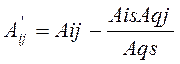
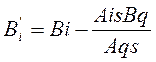
Далее перейти к п. III алгоритма.

 

Пример (решали как пример симплекс-метода):

F=2x1 + 3х2 à max при ограничениях: 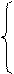  х1 + 3х2 <= 18 2х1 + х2 <= 16 х2 <= 5 3x1 <= 21 х1, х2 >= 0 Расширенная система имеет вид: 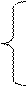х1 + 3х2 + х3 = 18 2х1 + х2 + х4 = 16 х2 + х5 = 5 3x1 + х6 = 21 х1, х2, х3, х4, х5, х6 >= 0 F - 2x1 - 3х2 = 0

Таблицы:

Базис Свободный член Переменные Оценочное отношение
Х1 Х2 Х3 Х4 Х5 Х6
Х3 18/3
Х4
Х5
Х6 ¥
F -2 -3  

 

Базис Свободный член Переменные Оценочное отношение
Х1 Х2 Х3 Х4 Х5 Х6
Х3 -3
Х4 -1 11/2
Х2 ¥
Х6
F -2  

 

Базис Свободный член Переменные Оценочное отношение
Х1 Х2 Х3 Х4 Х5 Х6
Х1 -3 ¥
Х4 -2 5/5
Х2 5/1
Х6 -3 12/9
F -3  

 

Базис Свободный член Переменные Оценочное отношение
Х1 Х2 Х3 Х4 Х5 Х6
Х1 -1/5 3/5  
Х5 -2/5 1/5  
Х2 2/5 -1/5  
Х6 3/5 -9/5  
F 4/5 3/5  

Метод искусственного базиса (М-метод)

Используется, когда первое БР – недопустимое.

В каждое уравнение, дающее отрицательную компоненту в БР, вводится своя новая неотрицательная искусственная переменная У1, У2, …, Ук, которая имеет тот же знак, что и свободный член в правой части уравнения. В первой таблице включаются в число основных (базисных) все искусственные переменные и те обычные добавочные переменные, которые определяют неотрицательные компоненты БР. Составляется новая линейная функция Т = F – М(У1 + У2 + … + Ук), где М – произвольно большое число, и ищется ее максимум. (Слайд 6)

Справедлива теорема (без доказательства):

1. Если в оптимальном решении новой функции все искусственные переменные = 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи (т.е. Тмах = Fмах, если У1=У2=…=Ук=0, т.е. минимум М-функции = 0) .

2. Если имеется оптимальное решение новой функции, в котором хотя бы одна из искусственных переменных отлична от 0, то система ограничений исходной задачи несовместна.

3. Если Тмах = ¥, то исходная задача также неразрешима, причем либо Fмах = ¥, либо условия задачи противоречивы.

 

Из теоремы следует, что сначала надо найти минимум М-функции. Если он = 0, то далее можно отбросить эти переменные и решать исходную задачу, исходя из полученного БР. На практике находят не минимум М-функции, а максимум (-М)-функции.

Пример:

F=x1 + 2х2 à max 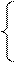х1 - х2 <= -1 х1 - х2 >= -3 х1 <= 3 х1, х2 >= 0   Расширенная система имеет вид: 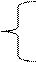х1 – х2 + х3 = -1 х1 - х2 - х4 = -3 х1 + х5 = 3 х1, х2, х3, х4, х5, х6 >= 0  

 

Х1= (0; 0; -1; 3; 3) – недопустимое БР, поэтому в первое уравнение введем искусственную переменную У1 с тем же знаком, что и свободный член.

х1 – х2 + х3 – у1= -1 х1 - х2 - х4 = -3 х1 + х5 = 3 - х1 + х2 - х3 + у1= 1 - х1 + х2 + х4 = 3 х1 + х5 = 3

 

В первой симплексной таблице последняя строка – это (-М)-функция, т.е. (-М)У1. Заполняется умножением строки У1 на коэффициент (-М).

 

(Слайд 7)
Базис

 Свободный член Переменные Оценочное отношение
Х1 Х2 Х3 Х4 Х5 У1
У1 -1 -1
Х4 -1
Х5 ¥
F -1 -2  
-Мф -М М -М М -М  

 

Заменяем У1 на Х2.

Базис Свободный член Переменные Оценочное отношение
Х1 Х2 Х3 Х4 Х5
Х2 -1 -1  
Х4  
Х5  
F -3 -2  
-Мф  

 

Последняя строка показывает, что критерий оптимальности выполнен: мах (-М) = 0, значит мин М = 0. далее эту строку можно не рассматривать. Получено ДБР (0; 1; 0; 2; 3), начиная с которого решаем исходную задачу в соответствии с обычным алгоритмом.