рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Программирование
- /
- Система m линейных уравнений с n переменными
Реферат Курсовая Конспект
Система m линейных уравнений с n переменными
Система m линейных уравнений с n переменными - раздел Программирование, Линейное программирование Система M Линейных Уравнений С N Переменными Имеет Вид: ...
Система m линейных уравнений с n переменными имеет вид:
 а11*Х1 + а12*Х2 + …+ а1j*Xj + …+ а1n*Xn = В1
а11*Х1 + а12*Х2 + …+ а1j*Xj + …+ а1n*Xn = В1
а21*Х1 + а22*Х2 + …+ а2j*Xj + … + а2n*Xn = В2
………………………….
аi1*Х1 + аi2*Х2 +…+ аij*Xj + … + а in*Xn = В i (6)
………………………….
аm1*Х1 + аm2*Х2 + … + аmn*Xn = Вm
или в краткой записи
 (I = 1, 2, …, m)
(I = 1, 2, …, m)
в задачах ЛП представляют интерес системы, в которых максимальное число независимых уравнений системы меньше числа переменных. Будем полагать, что в системе (6) все m уравнений системы независимы, т.е. m < n.
Любые m переменных системы m линейных уравнений с n переменными (m < n) называются основными (базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n - m переменных называются неосновными (или свободными).
Основными могут быть разные группы из n переменных, но общее число групп не превосходит число сочетаний 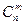 .
.
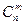 = n! / ((n-m)! m!)
= n! / ((n-m)! m!)
Пример:
Найти все возможные группы основных переменных в системе
 х1 – х2 – 2х3 + х4 = 0 (7)
х1 – х2 – 2х3 + х4 = 0 (7)
2х1 + х2 + 2х3 – х4 = 2
Решение. Общее число групп основных переменных не более чем  = 4*3/2 = 6, т.е. возможны группы основных переменных: х1, х2; х1, х3; х1, х4; х2, х3; х2, х4; х3, х4.
= 4*3/2 = 6, т.е. возможны группы основных переменных: х1, х2; х1, х3; х1, х4; х2, х3; х2, х4; х3, х4.
 Переменные х1, х2 могут быть основными, т.к. определитель матрицы из коэффициентов при этих переменных
Переменные х1, х2 могут быть основными, т.к. определитель матрицы из коэффициентов при этих переменных 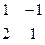 = 1 * 1 – 2 * (-1) = 3 ¹ 0. рассуждая аналогично, можно найти, что могут быть основными переменные х1, х3; х1, х4, но не могут быть основными х2, х3; х2, х4; х3, х4, т.к. соответствующие определители равны 0.
= 1 * 1 – 2 * (-1) = 3 ¹ 0. рассуждая аналогично, можно найти, что могут быть основными переменные х1, х3; х1, х4, но не могут быть основными х2, х3; х2, х4; х3, х4, т.к. соответствующие определители равны 0.
 х3, х4
х3, х4  = (-2) * (-1) – 2 * 1 = 0.
= (-2) * (-1) – 2 * 1 = 0.
Существует теорема. Если для системы из m линейных уравнений с n переменными ((m < n) существует хотя бы одна группа основных переменных, то эта система является неопределенной, причем каждому произвольному набору значений неосновных переменных соответствует одно решение системы.
Пусть, например, х1, х2, …, хm – основные переменные (если это не так, то нумерацию можно изменить), то определитель матрицы

 ¹ 0.
¹ 0.
Оставим в левых частях уравнений системы (6) члены с переменными х1, х2, …, хm, а члены с переменными xm+1, xm+2, …, xn перенесем в правые части. Получим:
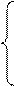
а11*Х1 + а12*Х2 + …+ а1m*Xm = В1 - а1m+1*Xm+1 - … - а1n*Xn
а21*Х1 + а22*Х2 + …+ а2m*Xm = В2 – а2m+1*Xm+1 - … - а2n*Xn
…………………………………………………………………….
аm1*Х1 + аm2*Х2 + …+ аmm*Xm = Вm - аmm+1*Xm+1 - … - аmn*Xn
Задавая неосновным переменным xm+1, xm+2, …, xn произвольные значения, каждый раз будем получать новую систему с новыми свободными членами. Каждая из полученных систем будет иметь один и тот же определитель, т.е. каждая из систем будет иметь единственное решение. Так как получаемых таким образом систем бесконечное множество, то и система (6) будет иметь бесконечное множество решений.
Решение Х = (х1, х2, …, хn) системы (6) называется допустимым, если оно содержит лишь неотрицательные компоненты, т.е. Хj >=0 для любых j = 1, 2, …, n. В противном случае решение называется недопустимым.
Среди бесконечного множества решений системы выделяют базисные решения.
Базисным решением (БР) системы m линейных уравнений с n переменными называют решение, в котором все n – m неосновных переменных равны нулю.
В задачах ЛП особый интерес представляют допустимые базисные решении (ДБР), или, как их еще называют, опорные планы. Число базисных решений является конечным, т.к. оно равно числу групп основных переменных, не превосходящему 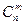 . Базисное решение, в котором хотя бы одна из основных переменных равна нулю, называется вырожденным.
. Базисное решение, в котором хотя бы одна из основных переменных равна нулю, называется вырожденным.
Пример:
В примере (7) существует три группы основных переменных, т.е. число базисных решений = 3.
Первое х1 и х2 – основные, х3 и х4 – неосновные (= 0), тогда
 х1 – х2 = 0
х1 – х2 = 0
2х1 + х2 = 2
откуда х1 =2/3; х2 = 2/3. следовательно первое баз решение системы Х1 = (2/3; 2/3; 0; 0) –допустимое.
Если взять за основные переменные Х1 и Х3, то получим второе баз решение системы Х2 = (2/3; 0; 2/3; 0) – также допустимое. Аналогично можно найти третье баз решение при основных переменных х1, х4 Х3 = (2/3; 0; 0; -2/3) – недопустимое.
Вывод: Совместная система (6) имеет бесконечно много решений, из них базисных решений – конечное число, не превосходящее 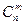 .
.
– Конец работы –
Эта тема принадлежит разделу:
Линейное программирование
А х а х a nxn b... при n является плоскостью а при n gt ее обобщением в n мерном...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Система m линейных уравнений с n переменными
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов