рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Программирование
- /
- Геометрический метод решения задач ЛП
Реферат Курсовая Конспект
Геометрический метод решения задач ЛП
Геометрический метод решения задач ЛП - раздел Программирование, Линейное программирование Итак, Выше Было Доказано, Что Множество Допустимых Решений (Многогранник Реше...
Итак, выше было доказано, что множество допустимых решений (многогранник решений) ЗЛП представляет собой выпуклый многогранник (или выпуклую многогранную область), а оптимальное решение задачи находится, по крайней мере, в одной из угловых точек многогранника решений.
Рассмотрим задачу в стандартной форме (1.4) – (1.6)
Найти такой план Х = (Х1, Х2, …, Хn) выпуска продукции, удовлетворяющий системе
 |
а11*Х1 + а12*Х2 + … + а1n*Xn <= В1
а21*Х1 + а22*Х2 + … + а2n*Xn <= В2 (1.4)
………………………….
аm1*Х1 + аm2*Х2 + … + аmn*Xn <= Вm
и условию Х1>=0, X2>=0, …, Xn>=0, (1.5)
при котором функция
F = С1*Х1 + С2*Х2 + … + Сn*Xn (1.6)
принимает макс значение.
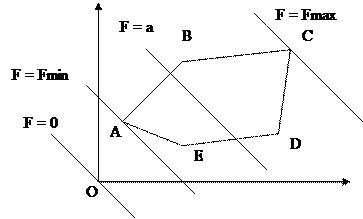 |
с двумя переменными (n=2). К такой форме может быть сведена и каноническая задача (с ограничениями в виде уравнений), когда число переменных n больше числа уравнений m на 2, т.е. n – m = 2.
ABCDE – геометрическое изображение системы ограничений. Необходимо среди точек этого многоугольника найти такую точку, в которой линейная функция F = С1*Х1 + С2*Х2 принимает макс или мин значение.
Рассмотрим линию, вдоль которой функция принимает одно и то же фиксированное значение а, т.е. F = а, или
с1*х1 + с2*х2 = а.
На многоугольнике решений следует найти точку, через которую проходит такая линия функции с наибольшим (при макс функции) или наименьшим (при мин функции) значением.
Уравнение линии с1*х1 + с2*х2 = а – это уравнение прямой линии. При различных значениях а линии будут параллельны, т.к. их угловые коэффициенты определяются соотношением между коэффициентами с1 и с2 и, следовательно равны.
Важное свойство линии уровня состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую – только убывает.
Может быть неограниченная прямоугольная область:
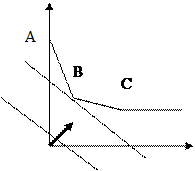 В данном примере есть мин, но нет макс.
В данном примере есть мин, но нет макс.
В вышеприведенных примерах макс и мин достигались в одной точке, т.е. задача имела единственное решение.
|

 Могут быть другие варианты:
Могут быть другие варианты:
 | |||||
 |
|
 |
На левом рисунке видно, что линия уровня с макс уровнем совпадает с граничной линией АВ многоугольника решений АВСD. Следовательно, на отрезке АВ линейная функция принимает одно и то же макс значение. Это значит, что задача имеет бесконечно много оптимальных решений (их задают координаты точек отрезка АВ), среди которых базисных оптимальных решений два – соответственно в угловых точках А и В. Точки отрезка АВ задаются уравнением соответствующей прямой, где с1 <= Х1<= c2.
При геометрическом решении подобных задач может быть неточность построения. Надо убедиться, что линия уровня совпадает с границей многоугольника решений. Это может быть, если они параллельны, т.е. их коэффициенты при переменных пропорциональны.
На правом рисунке показано, что если перемещать линию уровня в направлении убывания линейной функции, то она всегда будет пересекать многоугольник решений, т.е. линейная функция неограниченно убывает (нет конечного оптимума).
Если при геометрическом решении ЗЛП получен вариант, когда условия задачи противоречивы, т.е. область допустимых решений системы ограничений – пустое множество, то ясно, что оптимального решения нет и нет смысла строить линию уровня.
Плюсы геометрического метода:
§ прост,
§ нагляден,
§ быстро получить ответ.
Минусы геометрического метода:
§ возможны технические погрешности,
§ можно применять, когда в задаче только 2 переменных.
– Конец работы –
Эта тема принадлежит разделу:
Линейное программирование
А х а х a nxn b... при n является плоскостью а при n gt ее обобщением в n мерном...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Геометрический метод решения задач ЛП
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов