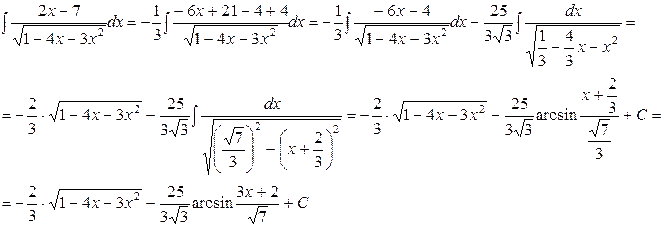Интегралы от некоторых функций, содержащих квадратный трехчлен.
Рассмотрим интеграл 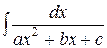 ( интеграл первого типа ). Преобразуем предварительно трехчлен, стоящий в знаменателе, представив его в виде суммы или разности квадратов:
( интеграл первого типа ). Преобразуем предварительно трехчлен, стоящий в знаменателе, представив его в виде суммы или разности квадратов:
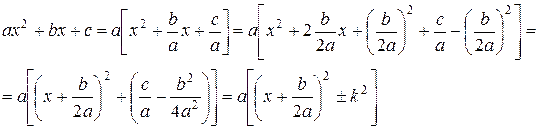
где 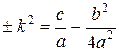 . Знак плюс или минус берется в зависимости от того, будет ли выражение, стоящее слева, положительное или отрицательным, т.е. будут ли корни трехчлена
. Знак плюс или минус берется в зависимости от того, будет ли выражение, стоящее слева, положительное или отрицательным, т.е. будут ли корни трехчлена 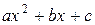 комплексными или действительными.
комплексными или действительными.
Таким образом, исходный интеграл принимает вид:
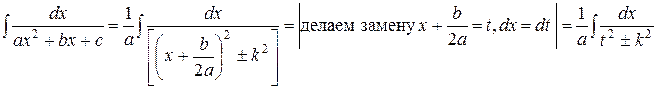 т.е. мы пришли к табличным интегралам.
т.е. мы пришли к табличным интегралам.
Пример 10. Вычислить интеграл 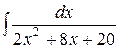 .
.
Решение:
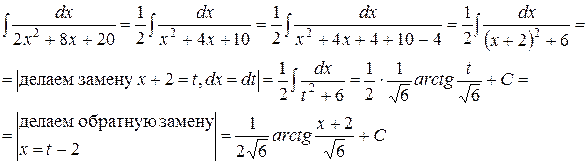
Рассмотрим интеграл более общего вида 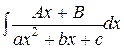 ( интеграл второго типа ). Произведем тождественное преобразование подынтегральной функции:
( интеграл второго типа ). Произведем тождественное преобразование подынтегральной функции:
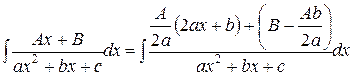
Последний интеграл представим в виде суммы двух интегралов. Вынося постоянные множители за знак интегралов, получим:
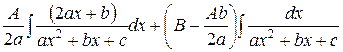
второй интеграл мы только что научились вычислять. Это интеграл первого типа. В первом интеграле сделаем замену переменного 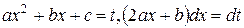 .
.
Следовательно, 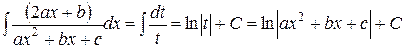 . Таким образом, окончательно получаем:
. Таким образом, окончательно получаем: 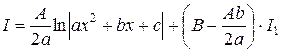 .
.
Пример 11. Вычислить интеграл 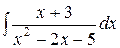 .
.
Решение:

Перейдем к усложненному варианту интеграла первого типа и рассмотрим интеграл 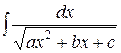 ( интеграл третьего типа ). Выполним преобразования, аналогичные преобразованиям проведенным с интегралом первого типа. Интеграл сведется, в зависимости от знака а, к табличным интегралам вида
( интеграл третьего типа ). Выполним преобразования, аналогичные преобразованиям проведенным с интегралом первого типа. Интеграл сведется, в зависимости от знака а, к табличным интегралам вида 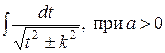 или
или 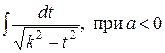 .
.
Пример 12. Вычислить интеграл 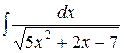 .
.
Решение: Выделив в знаменателе подынтегральной функции полный квадрат, получим
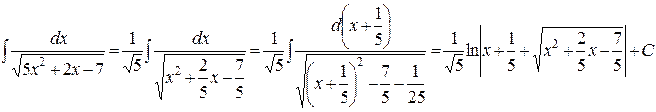
И наконец, интеграл 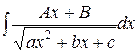 (интеграл четвертого типа). Он вычисляется с помощью преобразований, аналогичных проведенных в случае интеграла второго типа.
(интеграл четвертого типа). Он вычисляется с помощью преобразований, аналогичных проведенных в случае интеграла второго типа.
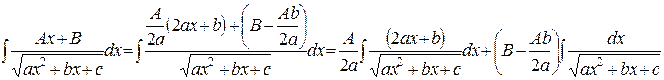
Применим к первому из полученных интегралов подстановку 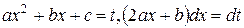 , получим
, получим
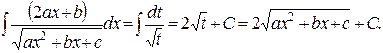
Второй же интеграл является уже рассмотренным интегралом третьего типа.
Пример 13. Вычислить интеграл  .
.
Решение: Представим данный интеграл в виде суммы двух интегралов, предварительно выделив в числителе подынтегральной функции слагаемое, равное производной подкоренного выражения из знаменателя: