Метод средних
Пусть эмпирическая формула имеет вид (2.35). Подставим в нее в место Х и Y опытные значения Xi и Yi. Так как левая часть формулы обычно не равна правой, получим систему уравнений:
| a∙X1 + b - Y1 = E1; a∙X2 + b - Y2 = E2; | (2.42) | |
| . . . . . . . . . a∙Xn + b - Yn = En; |
где Е1, Е2, . . . , Еn ,- невязки (отклонения), могут быть как положительными, так и отрицательными.
Согласно методу средних, за наилучшую эмпирическую зависимость принимается та, которая обеспечивает нулевое значение суммы отклонений по всем экспериментальным точкам, т.е. алгебраическая сумма невязок равна нулю.
Для определения параметров а и b формулы (2.35) поступают следующим образом:
1) Составляют условные Yi=a∙Xi + b, число которых m равно числу имеющихся собственных значений Хi и Yi .
2) Условные уравнения разбивают на примерные равные группы, число которых n равно числу определяемых коэффициентов (в данном случае - 2).
3) Уравнения, входящие в каждую из этих групп, складывают. Для данного случая получаем два уравнения:
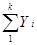 = a∙ = a∙ 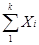 + k∙b; + k∙b;
| (2.43) | |
 = a∙ = a∙ 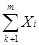 + (m-k) ∙b; + (m-k) ∙b;
| (2.44) |
4) Из этих уравнений находят неизвестные коэффициенты a и b.
Группировку условных уравнений перед их суммированием можно провести различными способами, причем каждый из них дает несколько отличающиеся значения коэффициентов. Рекомендуется группировать уравнения в порядке монотонного изменения одной из переменных.
Пример2.6: По опытным данным (табл. 2.11) определить коэффициенты эмпирической зависимости (2.37).
Для определения коэффициентов формулы (2.37) используем ее линейный вид (2.38) Значения переменных Y= ln(y) и t берутся из табл. 2.11 (строки 1 и 5). Имеющиеся 8 пар значений разбиваем на 2 группы и составляем для каждой группы по 4 условных уравнения Y = ln(a) + b.t:
4.054 = ln(a) + b.3 2.809 = ln(a) + b.15
3.735 = ln(a) + b.6 2.501 = ln(a) + b.18
3.434 = ln(a) + b.9 2.186 = ln(a) + b.21
3.122 = ln(a) + b.12 1.872 = ln(a) + b.24
Просуммировав почленно каждую группу, получим систему нормальных уравнений:
14.345 = 4.ln(a) + b.30
9.368 = 4.ln(a) + b.78
Решив систему, находим значение коэффициентов формулы (2.38), приведенной к линейному виду:
ln(a) = 4.3639 b = – 0.1037
Переходя к исходному виду формулы (2.37) и определив коэффициент а(а=78.563), получим окончательный видэмпирической формулы:
| y = 78.563.exp(–0.1037.b) | (2.45) |
Сравнение значений  Yi*, вычисленных по формуле (2.45), с опытными данными yi (табл. 2.11, строка 2) приведено в табл.2.13.
Yi*, вычисленных по формуле (2.45), с опытными данными yi (табл. 2.11, строка 2) приведено в табл.2.13.
Таблица 2.13
Оценка точности формулы (2.46)
| I | ti | yi | 
| D Y =  – yi – yi
| D Y 2 |
| 1 | 3 | 57.6 | 57.558 | –0.042 | 0.001764 |
| 2 | 6 | 41.9 | 42.169 | 0.269 | 0.072361 |
| 3 | 9 | 31.0 | 30.895 | –0.105 | 0.011025 |
| 4 | 12 | 22.7 | 22.635 | –0.065 | 0.004225 |
| 5 | 15 | 16.6 | 16.583 | –0.017 | 0.000289 |
| 6 | 18 | 12.2 | 12.150 | –0.050 | 0.00250 |
| 7 | 21 | 8.9 | 8.905 | –0.001 | 0.000001 |
| 8 | 24 | 6.5 | 6.521 | 0.021 | 0.000441 |
| S | SD Y 2= 0.09261 |
Как видно из сопоставления суммы квадратов отклонений (табл.2.12 и 2.13), меньшая погрешность обеспечивается при использовании метода средних по сравнению с методом выбранных точек.
В курсовой работе необходимо сравнить результаты, полученные при применении трех методов: выбранных точек, средних и наименьших квадратов.