Метод наименьших квадратов
Эмпирическая формула в общем виде может быть записана в следующем виде:
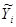 = F(Xi, aj), = F(Xi, aj),
| (2.13) |
где Хi — независимые переменные; aj — коэффициенты эмпирической зависимости.
Согласно методу наименьших квадратов наилучшими коэффициентами в смысле приближения к экспериментальным данным (yi=f(Xi)), будут коэффициенты, найденные из условия:
min{R(aj)} = 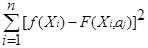 (i=1,2,...,n; j=0,1,...,m) (i=1,2,...,n; j=0,1,...,m)
| (2.14) |
т.е. минимума суммы квадратов отклонений между экспериментальными и расчетными значениями. В дальнейшем, вместо 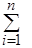 будем использовать Σ.
будем использовать Σ.
При фиксированных значениях Х функция R(aj) является положительно определенной (заданной и непрерывной в интервале [X1,Xn]) функцией и, следовательно, имеет экстремум. Необходимым условием существования экстремума функции нескольких переменных является равенство нулю частных производных.
Пусть эмпирическая формула имеет вид
F(Xi,a j) = a0 + a1.Xi + a2Xi2 + ... + am.Xim
Тогда выражение (2.13) можно записать в следующем виде:
| F(aj) =Σ (a0 + a1.Xi + a2Xi2 + ... + am.Xim – yi)2 | (2.15) |
Найдем частные производные функции R(a0, a1,...,am) по a0, a1,...,am и приравняем их к нулю. Получим так называемую нормальную систему m+1 уравнений с m+1 неизвестными a0, a1,...,am :
| ∂R/∂a0 = 2∑(a0 + a1Xi + a2Xi2 + ∙ ∙ ∙ + amXim - yi) ∙ 1 = 0 ∂R/∂a1 = 2∑(a0 + a1Xi + a2Xi2 + ∙ ∙ ∙ + amXim - yi) ∙ Xi = 0 ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∂R/∂am = 2∑(a0 + a1Xi + a2Xi2 + ∙ ∙ ∙ + amXim - yi) ∙ Xim = 0 | (2.16) |
Решив систему (2.16) известными методами (формулы Крамера, метод Гаусса и др.), найдем коэффициенты a0, a1,...,am формулы (2.14), которая будет обладать минимальным квадратичным отклонением R(aj ).
На практике, как правило, при определении коэффициентов с использованием метода наименьших квадратов любую эмпирическую зависимость целесообразно привести к линейному виду. Рассмотрим получение системы нормальных уравнений для этого случая.