ЗАДАЧА О КРАТЧАЙШЕМ ПУТИ НА СЕТИ. МЕТОД МИНТИ

Постановка задачи о кратчайшем пути на сети.

На сети, что задается графом (I,U), где И — множество вершин, U — множество дуг, с определенной на ней функцией стоимости сіj ((і,j) — дуга с U), для фиксированных i1 и is найти путь

L = ((i1,i2),(i2,i3)...,(is-1,is))

из вершины i1 в вершину is, длина которого

 

наименьшая.

Алгоритм метода Минти.

Методом Минти решается задача построения дерева кратчайших путей на сети с корнем в фиксированной вершине i1.

Алгоритм состоит из конечного числа шагов, на каждом из которых отражаются вершины сети и выделяются некоторые ее дуги.

Пусть Pr — множество вершин, обозначенных на шаге r, а Ir — множество вершин, обозначенных при r шагах.

ШАГ 0. Корень дерева (вершина i1) отражается постоянной h1=0; i1(h1)=i1(0). После нулевогошага P0={i1(0)}, I0={i1(0)}.

Пусть выполнено r шагов, за которые построенное множество

Ir={i1(0),...,ik(hk),...}

обозначенных вершин ik(hk), каждой из которых поставлено в соответствие число hk (численно ровное длине кратчайшего пути из вершины i1 в вершину ik).

ШАГ r+1. Строится разрез сети, который порождается множеством обозначенных вершин Ir, и определяется множество Jr={...,im,...} необозначенных вершин im сети, в которые заходят дуги разреза. Для каждой дуги (ik,im) разреза вычисляют сумму hk++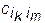и помечают те из дуг, для которых эта сумма минимальная. Потом выделяют обозначенные дуги так, чтобы в каждую необозначенную вершину множества Jr, в которое заходят обозначенные дуги разреза, заходила бы только одна выделенная дуга. После выделения дуг помечают вершины — концы выделенных дуг. Величина отметки ровная минимальной из сумм hk++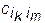, вычисленных для всех дуг разреза. Объединяя множество Ir с множеством Pr+1 вершин, обозначенных на (r+1) -м шаге, получают множество Ir+1 вершин, обозначенных при (r+1) шагах. Переходят к следующему шагу, если существует разрез, что порождается множеством Ir+1.

Указанный процесс продолжают до тех пор, пока возможное расширение множества обозначенных вершин.

Если некоторая вершина in сети осталась необозначенной по окончании процедуры Минти, то пути, что начинается в вершине i1 и заканчивается в вершине in, не существует.

Программное обеспечение.

Обучающий модуль, с помощью которого задача о кратчайшем пути на сети Решается в диалоге с пользователем за выложенным алгоритмом, вызывается из раздела «ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ» главного меню пакета ПО–МО.

Задание.

Решить методом Минти задачи о кратчайшем пути на сети, условия которых задаются модулем с помощью команды «Данные» главного меню (задачи №1–№9), а также следующие задачи, в каждой из которых сеть задается числом вершин N и матрицей L, что описывает множество дуг сети (каждый столбец этой матрицы отвечает существующей дуге сети, при этом, первый элемент столбца есть начало дуги, второе — конец дуги, третий — длина дуги):

1) N = 10, L =

1 1 1 2 2 2 3 3 4 4 5 5 5 6 6 7 7 8 9
2 3 4 3 5 6 4 6 6 7 8 9 10 5 9 6 9 10 10
5 10 20 5 20 17 12 17 5 4 10 6 20 7 5 1 5 11 15

2) N = 10, L =

1 1 2 2 3 3 3 4 4 5 5 6 6 7 7 7 8 8 9 9
2 3 4 5 2 7 8 3 7 9 10 5 10 6 8 9 4 9 6 10
20 12 9 20 12 20 7 20 2 10 18 10 18 1 7 16 18 17 20 8

3) N = 10, L =

1 1 1 2 2 2 3 4 4 4 4 5 5 6 7 7 7 8 8 9  
2 3 4 3 5 6 5 3 5 7 9 6 7 8 6 8 9 9 10 10  
18 20 19 8 2 11 2 7 1 6 12 9 5 12 6 15 6 16 2 4

4) N = 10, L =

1 1 1 2 2 2 3 3 4 4 4 5 5 5 6 6 7 8 9
2 3 4 4 5 6 2 4 5 7 8 7 9 10 5 9 8 10 10
15 2 20 9 20 17 13 12 15 8 5 4 3 7 7 11 5 6 4

5) N = 10, L =

1 1 2 2 2 3 3 3 3 4 4 5 5 6 6 7 7 8 9 10
2 3 4 5 6 2 6 7 8 5 9 6 9 7 9 9 10 7 10 8
13 2 8 18 2 11 13 20 20 10 20 4 20 20 20 11 20 11 14 5

6) N = 10, L =

1 1 1 1 2 2 3 3 3 3 4 4 5 5 6 7 7 8 8 9
2 3 4 5 3 6 4 6 7 10 7 8 4 8 10 9 10 7 9 10
10 18 20 20 8 15 9 7 17 12 8 10 7 15 5 10 19 20 10 2

Лабораторная работа 8.