Методы доказательства корректности рекурсивных программ

Рассмотрим следующую конкретизацию системы (4.36) определений рекурсивного кольца предикатов A₁, A₂,…, A_n:

A_j(t, x_j: y_j) º P_j(t, x_j) {K_j(t, x_j: y_j)} Q_j(t, x_j, y_j); j = 1…n; n > 0 . (5.17)

Здесь P_j и Q_j – предусловие и постусловие для предиката A_j; t – набор индукционных переменных; x_j, y_j – наборы переменных. На значениях набора t определен строгий частичный порядок ⊏, удовлетворяющий свойству обрыва бесконечных убывающих цепей; см. разд. 3.2. Пусть имеется предикат b(t), истинный, по меньшей мере, на любом минимальном элементе t. Предикат b(t) определяет базу индукции. Корректность определений рекурсивного кольца представлена формулой W(t) как корректность всех определений кольца:

W(t) º 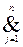{ P_j(t, x_j) Þ ($y_j. LS(K_j(t, x_j: y_j))) & (LS(K_i(t, x_j: y_j)) Þ Q_j(t, x_j, y_j)) }. (5.18)

Определим правила серии R доказательства корректности определений кольца (5.17) по методу структурной и полной индукции; см. разд. 3.2.

Правило RR1. b(t) ├ W(t).

Правило RR2. Øb(t) & Induct(t) ├ W(t).

Здесь Induct(t) @ "u. u ⊏ t Þ W(u). Предикат Induct(t) соответствует индукционному предположению при доказательстве по индукции и определяет корректность определений кольца (5.17) для всех значений, строго меньших t.

Лемма 5.9. Если правила RR1 и RR2 истинны, то определения кольца (5.17) корректны.

Доказательство. Конъюнкция правил RR1 и RR2 дает формулу (3.4) доказательства методом структурной индукции. □

Определим правила серии L. Выводимость программы рекурсивного кольца (5.17) из спецификаций представим формулой V(t):

V(t) º 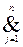{ P_j(t, x_j) & Q_j(t, x_j, y_j) Þ LS(K_i(t, x_j: y_j)) } . (5.19)

Правила доказательства корректности определений кольца (5.17) базируется на методе структурной индукции.

Правило LR1. b(t) ├ V(t).

Правило LR2. Øb(t) & Induct(t) ├ V(t).

Лемма 5.10. Допустим, для каждого предиката A_j рекурсивного кольца его спецификация (в виде предусловия P_j и постусловия Q_j) является реализуемой, а правая часть K_i - однозначной. Если правила LR1 и LR2 истинны, то определения кольца (5.17) корректны.

Доказательство. Конъюнкция правил LR1 и LR2 дает формулу (3.4) для доказательства истинности V(t) методом структурной индукции. Истинность V(t) есть истинность формулы (2.16) для всех предикатов рекурсивного кольца. Таким образом, все условия теоремы 2.1 удовлетворены, и поэтому все определения предикатов рекурсивного кольца являются корректными. □

Применимость леммы 5.10 базируется на однозначности операторов, используемых в определениях рекурсивного кольца (5.17). Однозначность операторов гарантируется в случае однозначности базисных предикатов по теореме 4.2.

Проиллюстрируем технику преобразования программы на языке CCP в эквивалентную программу на языке P3 на примере программы факториала, приведенной в разд. 4.11. Сначала используем функциональный стиль записи для операций и изображения констант. Получим:

A0(n: f) º A1( :c0, c1); A2(n, c0, c1: f)

A1( : c0, c1) º c0 = 0 || c1 = 1

A2(n, c0, c1: f) º b = (n = c0); A3(n, c1, b: f)

A3(n, c1, b: f) º if (b) f =c1 else A4(n, c1: f)

A4(n, c1: f) º n1 = n - c1; A5(n, n1: f)

A5(n, n1: f) º A0(n1: f1); f = n * f1

Далее подставим A1 в A0 и A5 в A4, а также преобразуем операторы суперпозиции к функциональному виду:

A0(n: f) º A2(n, 0, 1: f)

A2(n, c0, c1: f) º A3(n, c1, n = c0: f)

A3(n, c1, b: f) º if (b) f =c1 else A4(n, c1: f)

A4(n, c1: f) º A5(n, n - c1: f)

A5(n, n1: f) º f = n * A0(n1)

Подставим A3 в A2, а A2 в A0, A5 в A4:

A0(n: f) º if (n = 0) f =1 else A4(n, 1: f)

A4(n, c1: f) º f = n * A0(n - c1)

Наконец, подставляя A4 в A0, получим программу факториала на языке P3:

A0(n: f) º if (n = 0) f =1 else f = n * A0(n - 1) .

Использование функционального стиля и особенно подстановка определения предиката на место единственного вызова существенно улучшают структуру программы, за исключением последнего случая, в котором вызов A0(n - 1) находится в теле определения A0. Опыт показывает, что подавляющее число рекурсивных колец определений предикатов на языке P состоит из единственного рекурсивного определения.

Рассмотрим частный случай кольца (5.17) в виде следующего единственного рекурсивного определения:

A(t, x: y) º P_A(t, x) { if (j(t)) B(t, x: y) else C(t, x: y) } Q_A(t, x, y) . (5.20)

Здесь B(t, x: y) и C(t, x: y) обозначают блоки или вызовы, причем B(t, x: y) не зависит от A, а C(t, x: y) - зависит. При наличии спецификаций B и C можно было бы доказывать корректность представленного условного оператора по правилам RC1-RC4 или LC1, LC2, однако ввиду рекурсии следует использовать правила RR1, RR2. Формула корректности определения предиката (5.20) принимает вид:

W(t) º P_A(t, x) Þ ($y. LS(K(t, x: y))) & (LS(K(t, x: y)) Þ Q_A(t, x, y)) .

Здесь K(t, x: y) обозначает оператор if (j(t)) B(t, x: y) else C(t, x: y). Правила RR1, RR2 для кольца (5.20) принимают следующий вид.

Правило RR3. j(t) & P_A(t, x) ├ ($y. LS(B(t, x: y))) & (LS(B(t, x: y)) Þ Q_A(t, x, y)).

Правило RR4. Øj(t) & Induct(t) & P_A(t, x) ├

($y. LS(C(t, x: y))) & (LS(C(t, x: y)) Þ Q_A(t, x, y)).

В данных правилах истинность или ложность условия j(t) позволяет специализировать K(t, x:y) в виде B(t, x:y) или C(t, x:y). В итоге, справедлива следующая лемма.

Лемма 5.11. Если правила RR3 и RR4 истинны, то рекурсивное определение (5.20) корректно.

Аналогичным образом можно специализировать правила LR1, LR2 серии L. Формула корректности (5.20) принимает вид

V(t) º P_A(t, x) & Q_A(t, x, y) Þ LS(K(t, x: y)) .

Правила корректности получаются из правил LR1, LR2 для (5.20) применением специализации для K(t, x:y).

Правило LR3. j(t) & P_A(t, x) & Q_A(t, x, y) ├ LS(B(t, x: y)).

Правило LR4. Øj(t) & Induct(t) & P_A(t, x) & Q_A(t, x, y) ├ LS(C(t, x: y)).

Лемма 5.12. Допустим, спецификация (предусловие P_A(t, x) и постусловие Q_A(t, x, y)) является реализуемой, а вызовы (или блоки) B(t, x: y) и C(t, x: y) однозначны. Если правила LR3 и LR4 истинны, то определение (5.20) является корректным.

Доказательство. Из однозначности B(t, x: y) и C(t, x: y) получаем однозначность K(t, x:y). Выполняется условие леммы 5.10, что доказывает корректность (5.20). □

Техника доказательства корректности определений рекурсивного кольца базируется на замене каждого рекурсивного вызова A(u, x:y) в правой части рекурсивного определения на соответствующую спецификацию Q_A(u, x, y) с использованием индукционного предположения Induct(t). Если выполняется условие леммы 5.10 (или 5.12), то для u ⊏ t и при истинном предусловии P_A(u, x) по лемме 2.8 получаем тождество LS(A(u, x:y)) º Q_A(u, x, y), что дает возможность заменить вызов A(u, x:y) предикатом Q_A(u, x, y). В общем случае, когда однозначность спецификаций не гарантируется, применяется формула

LS(A(u, x:y)) Þ Q_A(u, x, y).

Пример 5.1. Программа умножения через сложение.

Докажем корректность следующего рекурсивного определения:

Умн(nat a, b: nat c) º

prea ≥ 0 & b ≥ 0

{ if (a = 0) c = 0 else c = b + Умн(a - 1, b) }

postc = a * b;

Доказательство. Реализуемость спецификации гарантируется, а однозначность правой части следует из теоремы 4.2. Чтобы применить лемму 5.12, достаточно доказать истинность правил LR3 и LR4. Правило LR3 принимает следующий вид:

LR3: a = 0 & & b ≥ 0 & c = a * b ├ c = 0.

Правило истинно ввиду свойства 0 * x = 0.

Правило LR4 переписывается в виде

LR4: a ¹ 0 & Induct(a) & a ≥ 0 & b ≥ 0 & c = a * b ├ c = b + Умн(a - 1, b).

Поскольку a ¹ 0 и a ≥ 0, то a – 1 ≥ 0, и истинно предусловие для вызова Умн(a - 1, b).
В соответствии с индукционным предположением, применяя лемму 2.8, можно заменить вызов на (a - 1) * b. Далее, b + (a - 1) * b = a * b, что доказывает истинность правила LR4 и корректность определения предиката Умн. □

Пример 5.2. Программа D(a, b: c) вычисления наибольшего общего делителя (НОД) положительных a и b.

Определим свойство «x является делителем a» следующим предикатом:

x – делитель a @ divisor(x, a) @ $z ≥ 0. x * z = a .

Предикат divisor2(с, a, b) @ divisor(с, a) & divisor(с, b) определяет с в качестве делителя значений a и b. Свойство наибольшего общего делителя определяется предикатом:

НОД(c, a, b) @ divisor2(с, a, b) & "x. (divisor2(x, a, b) Þ x ≤ c) .

Приведенная далее программа вычисления наибольшего общего делителя базируется на следующих известных свойствах НОД:

a = b Þ НОД(a, a, b) (5.21)

a > b & НОД(c, a, b) Þ НОД(c, a-b, b) (5.22)

НОД(c, a, b) º НОД(c, b, a) (5.23)

D(nat a, b: nat c) º pre a ≥ 1 & b ≥ 1

{ if (a = b) c = a

else if (a < b) D(a, b-a:c)

else D(a-b, b:c)

} post НОД(c, a, b);

Доказательство корректности программы D. Докажем реализуемость спецификации, т. е. истинность $c. НОД(c, a, b) для положительных a и b. Для a и b имеется, по крайней мере, один общий делитель - это 1. Следовательно, существует и наибольший общий делитель. Однозначность оператора в правой части определения D следует из теоремы 4.2.

Индуктивными переменными рекурсивного определения D является пара переменных a и b. На множестве положительных целых определим отношение

(a, b) ⊑ (c, d) @ a £ c & b £ d .

Отношение ⊑ является частичным порядком. Строгий частичный порядок ⊏ определяется на основе ⊑. Единственным минимальным элементом является (1, 1). Отношение a = b в условном операторе определения D является истинным на минимальном элементе и поэтому годится в качестве базиса при доказательстве по индукции. В соответствии с леммой 5.12 достаточно доказать истинность правил LR3 и LR4. Правило LR3 принимает следующий вид:

LR3: a = b & & a ≥ 1 & b ≥ 1 & НОД(c, a, b) ├ c = a .

Истинность правила следует из свойства (5.21) и единственности наибольшего общего делителя. Правило LR4 записывается в виде

LR4: a ¹ b & Induct(a, b) & a ≥ 1 & b ≥ 1 & НОД(c, a, b) ├

[ a < b Þ D(a, b - a :c) ] & [ Ø a < b Þ D(a - b, b :c) ] .

Пусть истинно a < b. Докажем истинность D(a, b - a :c). Так как b - a > 0, то для данного вызова истинно предусловие. Поскольку (a, b - a) ⊏ (a, b), то в соответствии с индуктивным предположением Induct(a, b) и по лемме 2.8 вызов D(a, b - a :c) тождественен НОД(c, a, b - a). Истинность НОД(c, a, b - a) следует из НОД(c, a, b) и свойств (5.22), (5.23).

Пусть истинно Ø a < b. Докажем истинность D(a - b, b :c). Из условий Ø a < b и a ¹ b следует b < a. Дальнейшее доказательство аналогично доказательству истинности первого конъюнкта левой части LR4. □

В приведенных примерах проводится следующая схема доказательства корректности рекурсивных определений вида (5.20). Сначала проверяется реализуемость спецификации и ее однозначность [19]. Проверяется, что все элементарные операции и вызываемые предикаты в правой части являются однозначными. Устанавливаются индуктивные переменные, определяется отношение частичного порядка и проверяется, что условие j в условном операторе покрывает все минимальные элементы. Далее, полагая истинным предусловие, постусловие и условие j, доказывается истинность первой альтернативы условного оператора. Затем для истинного предусловия, постусловия и ложного условия j доказывается истинность второй альтернативы условного оператора. При этом для каждого рекурсивного вызова проверяется истинность предусловия для аргументов вызова. Доказывается, что аргументы, соответствующие индуктивным переменным, строго меньше в смысле выбранного отношения. Это дает возможность заменить рекурсивный вызов соответствующим постусловием.