Гиперфункции

Пример 7.2. Допустим, для списка s целых чисел требуется извлечь второй элемент и присвоить переменной e. Список может содержать менее двух элементов. Логическая переменная exist = true, если второй элемент существует. Вычисление переменных e и exist можно представить следующим определением:

elemTwo(list(int) s: int e,bool exist ) (7.12)

{ if (s = nil Ú s.cdr = nil) exist = false

else { e = s.cdr.car || exist = true}

} post exist = (s ¹ nil & s.cdr ¹ nil) & (exist Þ e = s.cdr.car)

Предположим, имеется фрагмент программы с вызовом предиката elemTwo и последующими вызовами предикатов B и D, причем e используется среди аргументов B:

elemTwo(s: e,exist); if(exist) B(e…) else D(…) (7.13)

Подставим тело elemTwo на место вызова. Внесем оператор if(exist) A(e…) else (…) в обе альтернативы первого условного оператора:

if ( s = nil Ú s.cdr = nil) (7.14)

{ exist = false; if(exist) B(e…) else D(…) }

else { { e = s.cdr.car || exist = true}; if(exist) B(e…) else D(…) }

Далее реализуется специализация, позволяющая заменить внесенный условный оператор одной из альтернатив:

if (s = nil Ú s.cdr = nil) { exist = false || D(…) }

else { { e = s.cdr.car || exist = true}; B(e…) }

Обнаруживается, что переменная exist становится ненужной. Устраняя ее, получим результат подстановки тела elemTwo на место вызова в более компактном виде:

if (s = nil Ú s.cdr = nil) D(…) else { e = s.cdr.car; B(e…) } (7.15)

В данном примере определение (7.12) выглядит неадекватным и громоздким. Адекватным можно считать лишь итоговый оператор (7.15). Другой недостаток: переменная e не определена для списков, содержащих менее двух элементов. Неудобные ситуации, аналогичные приведенной в примере 7.2, регулярно встречаются в процессе программирования.

Проблему, представленную в примере 7.2, рассмотрим в общем виде. Пусть имеется тройка Хоара P(x) { A(x: y, z) } Q(x, y, z), где x, y и z - непересекающиеся, возможно пустые, наборы переменных. Предикат Q(x, y, z) определяется следующим тождеством:

Q(x, y, z) @ (C(x) Þ S(x, y)) & (ØC(x) Þ R(x, z)) (7.16)

Предикаты S(x, y) и R(x, z) можно рассматривать как функции S: x ® y и R: x ® z. В случае, когда условие C(x) истинно, предикат Q(x, y, z) совпадает с функцией S: x ® y, а при ложном условии C(x) - с функцией R: x ® z. Будем считать, что область определения каждой из функций имеет непустое пересечение с областью истинности предусловия P(x). Таким образом, Q(x, y, z) является результатом склеивания двух функций S: x ® y и R: x ® z. В предикате Q(x, y, z) не определено значение набора z, если C(x) истинно. Аналогично не определено значение y при ложном C(x).

Лемма 7.10. Если предикат S(x, y) реализуем в области P(x) & C(x), а R(x, z) - в области P(x) & ØC(x), то спецификация предиката A(x: y, z) является реализуемой.

Лемма 7.11. Если предикат S(x, y) является однозначным в области P(x) & C(x), а R(x, z) - в области P(x) & ØC(x), то спецификация предиката A(x: y, z) вляется однозначной.

Пусть вызов предиката A используется во фрагменте вида

A(x: y, z); if(C(x)) B(y: u) else D(z: u) . (7.17)

Вычисление C(x) может оказаться достаточно трудоемким. Очевидно, что значение C(x) можно вычислить внутри определения предиката A. Введем логическую переменную c и следующим образом инструментируем определение предиката A, превратив его в A’(x: c, y, z). Если некоторая ветвь тела предиката A завершается присваиванием набору y, то в конце этой ветви вставляется оператор c = true; если ветвь завершается вычислением z, то в конце ее вставляется c = false. Тогда фрагмент (7.17) можно заменить более эффективным:

A’(x: c, y, z); if(c) B(y: u) else D(z: u) . (7.18)

Пример 7.3. Необходимость использования предиката A’ вместо A рассмотрим на примере задачи решения системы линейных уравнений:

LinEq(n, a, x, b) @ 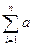_ij x_j, = b_j; j = 1..n.

Спецификацию задачи представим описаниями:

type VEC(nat k) = array (real, 1..k);

type MATRICE(nat k) = array (real, 1..k, 1..k);

Lin(nat n, MATRICE(n) a, VEC(n) b: VEC(n) x)

pre det(n, a) ¹ 0 [20]

post LinEq(n, a, x, b);

В предусловии функция det(n, a) обозначает детерминант матрицы. Истинное предусловие определяет невырожденность системы уравнений и гарантирует существование решения, т. е. реализуемость приведенной спецификации.

Иногда требуется решить более общую задачу:

Lin1(nat n, MATRICE(n) a, VEC(n) b: bool c; VEC(n) x)

post c = (det(n, a) ¹ 0) & (c Þ LinEq(n, a, x, b));

Предусловие предиката Lin1 по форме соответствует (7.16) c пустым предикатом R и S = LinEq. Переменная c вычисляет условие det(n, a) ¹ 0, аналогичное C(x) в (7.17). Использование Lin1 в программе реализуется в составе следующего фрагмента вида (7.18):

Lin1(n, a, b: c; x); if(c) B(x…) else D(…) .

В данном фрагменте вычисление c в Lin1 позволяет избежать повторного вычисления det(n, a).

Рассмотрим процесс подстановки определения A’ на место вызова во фрагменте (7.18) с последующим упрощением аналогично тому, как это делалось для фрагмента (7.13). Обнаруживается, что втягивание условного оператора внутрь подставленного тела A’ аналогично (7.14) с последующей специализацией может привести к появлению нескольких копий вызовов B(y…) и D(z…). Поэтому применим другое преобразование. Альтернативы условного оператора пометим метками 1 и 2. Получим оператор

if(c) 1: B(y: u) else 2: D(z: u) . (7.19)

Далее в подставленном теле A’ всякий оператор c = true заменим на #1, а c = false - на #2. Операторы #1 и #2 обозначают операторы перехода goto 1 и goto 2, соответственно. Например, применение данного преобразования для (7.13) дает следующий фрагмент:

if ( s = nil Ú s.cdr = nil) #1

else { e = s.cdr.car; #2};

if(exist) 1: B(e…) else 2: D(…)

Модифицированный фрагмент (7.18) запишем в виде

A’’(x: y, z); if(c) 1: B(y: u) else 2: D(z: u) . (7.20)

Здесь A’’ обозначает блок, полученный после подстановки определения A’ и замены c = true и c = false на #1 и #2. Поскольку в A’’ нет переменной c, заменим оператор (7.19) последовательностью

1: B(y: u); goto 3; 2: D(z: u); 3: . (7.21)

Композицию вида (7.21) с двумя (или более) входами и слиянием ветвей, соответствующих разным входам, запишем в следующем виде:

case 1: B(y: u) case 2: D(z: u) . (7.22)

Каждый из операторов case 1: B(y: u) и case 2: D(z: u) называется оператором продолжения ветви, или, коротко, оператор-ветвь. Последовательность из одного или более операторов продолжения ветвей называется обработчиком ветвей. Обработчику ветвей предшествует оператор - вызов гиперфункции или блок, содержащий операторы перехода. Если предшествующий оператор нормально завершается (не оператором перехода), то обработчик ветвей пропускается - исполнение продолжается с оператора, следующего за обработчиком.

Отметим, что оператор (7.19) эквивалентен

if(c) #1 else #2; case 1: B(y: u) case 2: D(z: u) . (7.23)

Отметим также, что блок A’’(x: y, z) эквивалентен композиции

A’(x: c, y, z); if(c) #1 else #2 . (7.24)

В итоге, исходный фрагмент (7.17) эквивалентен следующему:

A’’(x: y, z) case 1: B(y: u) case 2: D(z: u) . (7.25)

Исходный предикат A(x: y, z) будем записывать в виде A(x: y #1: z #2) и называть гиперфункцией с двумя ветвями. Метки 1 и 2 являются метками ветвей. Определение гиперфункции A(x: y #1: z #2) записывается следующим образом:

A(x: y #1: z #2) pre P(x); pre 1: C(x) (7.26)

{ A’’(x: y, z) } post 1: S(x, y); post 2: R(x, z);

Здесь блок A’’(x: y, z) является телом определения гиперфункции; P(x) - общим предусловием; C(x) - предусловием первой ветви гиперфункции; S(x, y) - постусловием первой ветви; R(x, z) - постусловием второй ветви. Фрагмент (7.17) записывается следующим образом:

A(x: y #1: z #2) case 1: B(y: u) case 2: D(z: u) . (7.27)

Для композиции (7.27) допускается более компактная запись:

A(x: y : z) case B(y: u) case D(z: u) . (7.28)

Вернемся к примеру 7.2 и дадим определение предиката elemTwo в виде гиперфункции:

elemTwo(list(int) s: int e:)

pre 1: s ¹ nil & s.cdr ¹ nil

{ if (s = nil Ú s.cdr = nil) #2

else { e = s.cdr.car #1}

} post 1: e=s.cdr.car;

Заголовок гиперфункции elemTwo(list(int) s: int e:) без указания меток ветвей подразумевает elemTwo(list(int) s: int e #1:#2). Отметим, что постусловие второй ветви отсутствует: оно считается тождественно истинным. Композиция фрагмента (7.13) записывается в новых обозначениях следующим образом:

elemTwo(s: e: ) case B(e…) case D(…) .

Допустим, имеется определение предиката:

V(x, u) @ pre P_V(x) { A(x: y : z) case B(y: u) case D(z: u) } post Q_V(x, u); (7.29)

Гиперфункция A имеет определение (7.26). Предикаты B и D представлены тройками Хоара:

{P_B(y)} B {Q_B(y, u)}, {P_D(z)} D {Q_D(z, u)},

Поскольку фрагмент (7.28) эквивалентен (7.17), определение (7.29) эквивалентно

V(x, u) @ pre P_V(x) {A(x: y, z); if(C(x)) B(y: u) else D(z: u)} post Q_V(x, u); (7.30)

Здесь предикат A определяется тройкой Хоара P(x) { A(x: y, z) } Q(x, y, z), где Q(x, y, z) представлена формулой (7.16). Определим предикат:

H(x, y, z, u) @ pre P_H(x, y, z ){if(C(x)) B(y: u) else D(z: u)} post Q_H(x, y, z, u) .

Тогда получим следующие формулы для предусловия и постусловия предиката H:

P_H(x, y, z) @ (C(x) Þ P_B(y)) & (ØC(x) Þ P_D(z))

Q_H(x, y, z, u) @ (C(x) Þ Q_B(y, u)) & (ØC(x) Þ Q_D(z, u)) .

Определение (7.30) эквивалентно следующему:

V(x, u) @ pre P_V(x) {A(x: y, z); H(x, y, z, u)} post Q_V(x, u); (7.31)

Построим правила RS1 и RS2 для суперпозиции в определении (7.31). Получим следующие правила.

Правило RS1’. P_V(x) ├ P(x) & "y,z (Q(x, y, z) Þ P_H(x, y, z )) .

Правило RS2’. P_V(x) & $y,z (Q(x, y, z) & Q_H(x, y, z, u)) ├ Q_V(x, u) .

Далее подставим формулы для Q, P_H и Q_H. Получим следующие правила.

Правило RS1’’. P_V(x) ├ P(x) & "y,z ((C(x) Þ S(x, y)) & (ØC(x) Þ R(x, z)) Þ

(C(x) Þ P_B(y)) & (ØC(x) Þ P_D(z)))

Правило RS2’’. P_V(x) & $y,z ((C(x) Þ S(x, y)) & (ØC(x) Þ R(x, z)) &

(C(x) Þ Q_B(y, u)) & (ØC(x) Þ Q_D(z, u))) ├ Q_V(x, u)

Специализация по условию C(x) дает следующие правила.

Правило RS9. P_V(x)├ P(x) .

Правило RS10. P_V(x) & C(x)├ "y (S(x, y) Þ P_B(y)) .

Правило RS11. P_V(x) & ØC(x)├ "z (R(x, z) Þ P_D(z)) .

Правило RS12. P_V(x) & C(x) & $y (S(x, y) & Q_B(y, u)) ├ Q_V(x, u) .

Правило RS13. P_V(x) & ØC(x) & $z (R(x, z) & Q_D(z, u)) ├ Q_V(x, u) .

В итоге, справедлива следующая лемма.

Лемма 7.12. Пусть предусловие P_V(x) истинно. Допустим, предикаты A, B и D корректны. Если правила RS9-RS13 истинны, то предикат V, представленный определением (7.29), является корректным.

Построим правила серии L для композиции (7.29), в которой используется гиперфункция. Для суперпозиции (7.31) построим правила LS1 и LS2.

Правило LS1’. P_V(x) ├ P(x) .

Правило LS2’. P_V(x) & Q_V(x, u) & Q(x, y, z) ├ P_H(x, y, z) & Q_H(x, y, z, u) .

Для правила LS2’ подставим формулы для Q, P_H и Q_H. Получим правило LS2’’.

Правило LS2’’. P_V(x) & Q_V(x, u) & (C(x) Þ S(x, y)) & (ØC(x) Þ R(x, z)) ├

(C(x) Þ P_B(y)) & (ØC(x) Þ P_D(z)) & (C(x) Þ Q_B(y, u)) & (ØC(x) Þ Q_D(z, u)).

Специализация по условию C(x) дает следующие правила.

Правило LS10. P_V(x) ├ P(x) .

Правило LS11. P_V(x) & Q_V(x, u) & C(x) & S(x, y) ├ P_B(y) & Q_B(y, u) .

Правило LS12. P_V(x) & Q_V(x, u) & ØC(x) & R(x, z) ├ P_D(z) & Q_D(z, u) .

Лемма 7.13. Допустим, спецификация предиката V реализуема, предикаты A, B и D однозначны в области предусловий и корректны, а их спецификации однозначны. Если правила LS10, LS11 и LS12 истинны, то предикат V, представленный определением (7.29), является корректным.

Приведенные правила серий R и L для композиции (7.29), в которой используется гиперфункция, демонстрируют, что доказательство проводится раздельно для каждой ветви гиперфункции аналогично тому, как это делается для условного оператора. При этом доказательство для каждой из ветвей гиперфункции проводится как для суперпозиции.

Пример 7.4. Определим гиперфункцию Comp следующей спецификацией:

Comp(list(int) s: : int d, list(int) r)

pre 1: s = nil

post 2: d = s.car & r = s.cdr;

Построим определение предиката elemTwo из примера 7.2 через гиперфункцию Comp, не используя полей car, cdr и конструктора nil.

elemTwo(list(int) s: int e #1:#2)

pre 1: s ¹ nil & s.cdr ¹ nil

{ int e1; list(int) s1, s2;

Comp(s: : e1, s1)

case #2

case {

Comp(s1: : e, s2)

case#2

case#1

}

} post 1: e = s.cdr.car;

Если оператор продолжения ветви содержит только оператор перехода, то действует следующее правило: оператор-ветвь устраняется, а оператор перехода переносится в конец соответствующей ветви вызова гиперфункции. Определение гиперфункции elemTwo переписывается следующим образом:

elemTwo(list(int) s: int e #1:#2)

pre 1: s ¹ nil & s.cdr ¹ nil

{ Comp(s: #2: int e1, list(int) s1)

case Comp(s1: #2: e, list(int) s2 #1);

} post 1: e = s.cdr.car;

В данном определении elemTwo, кроме переноса указателей завершения, реализован перенос описаний локальных переменных e1, s1 и s2 в позиции их определения, т. е. места в программе, где им присваиваются значения.

Если обработчик ветвей состоит из единственного оператора продолжения ветви, а предшествующий оператор не имеет нормального завершения исполнения, то обработчик ветвей вырождается. В этом случае оператор продолжения ветви устраняется, а находящийся в нем оператор композируется с предыдущим оператором в виде оператора суперпозиции. Последнее определение elemTwo должно быть заменено следующим:

elemTwo(list(int) s: int e #1:#2)

pre 1: s ¹ nil & s.cdr ¹ nil

{ Comp(s: #2: _, list(int) s1);

Comp(s1: #2: e, _ #1);

} post 1: e = s.cdr.car;

Дополнительно в этом определении проведена замена результирующих вхождений локальных переменных e1 и s2 стандартным именем “_”, означающим, что соответствующий результат игнорируется при исполнении.

Допустим, имеется условный оператор вида

if (C) {A; B} else {E; D} . (7.32)

Определим гиперфункцию:

H(…: …: …) º { if (C) {A; #1} else {E; #2}} .

Тогда условный оператор (7.32) эквивалентен следующей композиции:

H(…: …: …) case B case D .

Данное свойство демонстрирует гибкость аппарата гиперфункций. С помощью гиперфункций можно произвольно декомпозировать программу. Такое не реализуется традиционными средствами.

Стиль программирования с использованием гиперфункций проиллюстрируем на примере следующей задачи.

Пример 7.5. Сумма чисел в строке. Имеется строка литер, в которой встречаются числа в виде списка десятичных цифр. Числа разделяются произвольным набором литер, отличных от цифр. Подсчитать сумму чисел в строке.

Спецификацию задачи представим определением:

СуммаСтроки(string s: nat n) post P(s, n);

Предикат P(s, n) определяется рекурсивным образом.

цифра(charc) @ c Î {’0’, ’1’, ’2’, ’3’, ’4’, ’5’, ’6’, ’7’, ’8’, ’9’};

число(string s) @ s ¹ nil & "s1,s2Îstring "cÎchar (s = s1 + c + s2 Þ цифра(c))

val(string s: nat n) @ pre число(s) post n - значение числа s.

P(string s, nat n) @

(s = nil Þ n = 0) &

& (число(s) Þ n = val(s))

& ("s1Îstring "cÎchar. Øцифра(c) & s = c + s1 Þ P(s1, n)) &

& ("s1,s2Îstring "cÎchar. Øцифра(c) & число(s1) & s = s1 + c + s2 Þ

$m. P(s2, m) & n = val(s1) + m)

Напомним, что тип string есть list(char), а операция “+” обозначает конкатенацию строк.

Лемма 7.14. Спецификация предиката P реализуема.

Доказательство проводится индукцией по длине строки s. □

Так же, как и для программы УмнO (см. разд. 7.4), для построения алгоритма с хвостовой формой рекурсии необходимо обобщение исходной задачи введением накопителя для суммирования:

Сумма(string s, nat m: nat n) post $x. P(s, x) & n = m + x;

Ввиду истинности тождества СуммаСтроки(s: n) º Сумма(s, 0: n) корректно следующее определение предиката:

СуммаСтроки(string s: nat n) º {Сумма(s, 0: n)} post P(s, n);

Алгоритм решения данной задачи очевиден. Сначала в строке находится первая цифра. Далее вычисляется число, начинающееся с этой цифры. Для оставшейся части строки действие алгоритма повторяется. При нахождении первой цифры возможна ситуация, когда строка не содержит цифр. Данную ситуацию обозначим предикатом

мусор(string s) @ "s1,s2Îstring "cÎchar (s = s1 + c + s2 Þ Øцифра(c)) .

В частности, предикат истинен для пустой строки. Определение первой цифры выражается гиперфункцией:

перваяЦифра(string s: : char e, string r)

pre 1: мусор(s)

post 2: $w. мусор(w) & s = w + e + r & цифра(e);

Лемма 7.15. Спецификация гиперфункции перваяЦифра реализуема.

Отметим, что можно было бы использовать гиперфункцию вида перваяЦифра1(string s: : string r), где r начинается с первой цифры, однако в реализации это приведет к повторному доступу к одной и той же литере в строке. В практике типичным является решение, которое можно представить предикатом

перваяЦифра2(string s: char e, string r) .

Здесь отсутствие цифр в строке s кодируется некоторым значением e, отличным от цифры. Это типичный программистский трюк, усложняющий семантику переменной e и логику программы в целом. Вред подобных трюков обычно проявляется для сложных программ. Отметим, что решение в виде гиперфункции дает более короткую и эффективную программу.

Вторая часть алгоритма - выделение числа в строке и его вычисление - представляется предикатом:

числоВстроке(char e, string r: nat v, string t)

pre цифра(e)

post $w. конецЧисла(r, w, t) & v = val(e + w);

конецЧисла(r, w, t) @ r = w + t & (w = nil Ú число(w)) & (t = nil Ú Øцифра(t.car);

Лемма 7.16. Спецификация предиката числоВстроке реализуема.

Дадим определение предиката Сумма и докажем его корректность.

Сумма(string s, nat m : nat n)

{ перваяЦифра(s: : char e, string r)

case n = m

case {числоВстроке(e, r: nat v, string t); Сумма(t, m + v:n)}

} post $x. P(s, x) & n = m + x

Доказательство. Докажем истинность правила LS11. Пусть истинны формулы: мусор(s), $x. P(s, x) & n = m + x. Необходимо доказать, что n = m, т. е. истинно P(s, 0). Истинность P(s, 0) доказывается индукцией по длине строки s. Докажем истинность правила LS12. Пусть истинны формулы:

$x. P(s, x) & n = m + x, $w. мусор(w) & s = w + e + r & цифра(e), Øмусор(s) . (7.33)

Необходимо доказать истинность второго оператора продолжения ветви, представляющего суперпозицию вызовов предикатов числоВстроке и Сумма. Поскольку истинно предусловие вызова числоВстроке, присоединим его постусловие к формулам (7.33) и докажем истинность рекурсивного вызова Сумма(t, m + v:n). Индуктивной переменной является первый аргумент. Используется следующее отношение порядка: t ⊑ s @ $w. w + t = s. Минимальный элемент nil покрывается условием мусор(s), которому соответствует первый оператор продолжения ветви: для s = nil доказательство корректности уже проведено.

Из второй формулы (7.33) следует, что s = q + e + r для некоторого q. Из постусловия числоВстроке следует, что r = w + t. Тогда s = q + e + w + t и t ⊏ s. В соответствии с индукционным предположением вызов Сумма(t, m + v:n) эквивалентен его постусловию:

$y. P(t, y) & n = m + v + y . (7.34)

Докажем истинность (7.34). Пусть истинны P(s, x) и P(t, y). Достаточно доказать, что x = v + y. При этом истинны s = q + e + w + t, мусор(q) и w = nil Ú число(w). Легко доказать, что истинно число(e + w). Тогда применима функция val(e + w). Из постусловия числоВстроке следует, что v = val(e + w). Индукцией по длине q доказывается истинность P((e + w) + t, x). Наконец, истинность x = v + y следует из определения предиката P. □

Дадим определение гиперфункции перваяЦифра и докажем его корректность.

перваяЦифра(string s: : char e, string r) pre 1: мусор(s)

{ if (s = nil) #1

else {

{ char a = s.car || string u = s.cdr };

if (цифра(a)) { r = u ||e = a #2}

else перваяЦифра(u: #1 : e, r #2)

}

} post 2: $w. мусор(w) & s = w + e + r & цифра(e);

Доказательство. Пусть истинна спецификация гиперфункции, т. е. формула

Øмусор(s) Þ $w. мусор(w) & s = w + e + r & цифра(e) (7.35)

Докажем истинность тела гиперфункции. Пусть истинно условие s = nil. Тогда истинно предусловие первой ветви мусор(s), что подтверждает истинность оператора перехода #1. Пусть истинно s ¹ nil. Докажем истинность блока после else. Истинны корректно использование полей car и cdr. Поэтому достаточно доказать истинность внутреннего условного оператора при a = s.car и u = s.cdr. Пусть истинно условие цифра(a). Поскольку s = a + u, то ложно мусор(s) и из (7.35) следует s = w + e + r & мусор(w) & цифра(e). Тогда w = nil, e = a и r = u. Поскольку истинен оператор перехода #2, то блок {r = u ||e = a #2} является истинным. Пусть истинно условие Øцифра(a). Докажем истинность рекурсивного вызова. Поскольку u ⊏ s, а для s = nil корректность гиперфункции доказана, то рекурсивный вызов можно заменить постусловием:

Øмусор(u) Þ $q. мусор(q) & u = q + e + r & цифра(e) . (7.36)

Докажем истинность (7.36). Пусть истинна Øмусор(u). Тогда истинны Øмусор(s) и правая часть импликации (7.35). Поскольку s = a + u и Øцифра(a), то w = a + q для некоторого q и истинно мусор(q). Это доказывает формулу (7.36). □

Чтобы получить хвостовую рекурсию для предиката числоВстроке, необходимо ввести накопитель для вычисления значения очередного числа. Определим предикат:

взятьЧисло(string r, nat p: nat v, string t) º

post $w. конецЧисла(r, w, t) & val1(w, p, v);

val(s: n) º pre число(s) post val1(s, 0, n);

val1(w, p, n) º (w = nil Þ n = p) & (w ≠ nil Þ val1(w.cdr, p * 10 + valD(w.car), n) ,

где valD(e) - значение цифры e. Тогда корректно следующее определение предиката:

числоВстроке(char e, string r: nat v, string t)

pre цифра(e)

{ взятьЧисло(r, val(e): v, t) }

post $w. конецЧисла(r, w, t) & v = val(e + w);

Дадим определение предиката взятьЧисло и докажем его корректность.

взятьЧисло(string r, nat p: nat v, string t)

{ if (r = nil) {v = p || t = r}