Свертки - раздел Информатика, ЭТАПЫ ОБРАЩЕНИЯ ИНФОРМАЦИИ
В Одном Измерении Интеграл Свертки Двух Функций F(Х)...
В одном измерении интеграл свертки двух функций f(х)и g(х) определяется как:
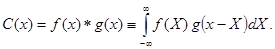
(2.4)
Путем простой замены переменных находим:

(2.5)
Для двух или более измерений можно воспользоваться векторной формой:

(2.6)
Тождественной операцией является свертка с дельта-функцией Дирака:
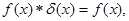
(2.7)
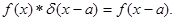
Пример свертки дает принцип Гюйгенса, записанный в виде формул Кирхгофа. Каждая точка фронта волны рассматривается как источник сферической волны, начальная амплитуда которой пропорциональна амплитуде падающей волны, Затем амплитуды вторичных волн складываются и дают амплитуду в плоскости наблюдения. Таким образом, функция амплитуды g(x, у) на начальном фронте волны рассеивается с помощью функции, которая представляет вторичную сферическую волну от точечного источника на фронте волны.
Для дифракции Френеля в малоугловом приближении записать:

(2.10)
Функцию в квадратных скобках можно назвать функцией распространения, или волновой функцией точечного источника, q(х, у) =d(х, у).
ЧАСТОТНАЯ ФОРМА ПРЕДСТАВЛЕНИЯ СИГНАЛА
Любой физически реализуемый сигнал ограничен во времени и обладает конечной энергией. Функции, отображающие реальные сигналы, удовлетворяют условиям Дирихле и абсолютно интегрируемы, т. е.
 (1.40)
(1.40)
где М — конечная величина.
Модели таких сигналов также могут быть представлены совокупностью гармонических составляющих в соответствии с выражением (1.2). Конкретный вид спектрального преобразования для непериодического сигнала получим, проследив изменения, происходящие в спектре периодической последовательности импульсов ii(f) при увеличении периода их повторения.
Пару преобразований Фурье для периодической функции u1(t) запишем в форме (1.15) и (1.16):
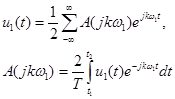
При Т® ¥ u1(t) переходит в u(t), частота w1 уменьшается до dw, a kw1 превращается в текущую частоту w. Заменяя суммирование интегрированием, находим
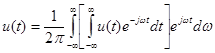
Обозначив интеграл в квадратных скобках S(jw), получим формулы для прямого и обратного интегрального преобразования Фурье:
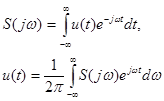 (1.41-1.42)
(1.41-1.42)
Величину S(jw) называют комплексной спектральной плотностью или спектральной характеристикой. Она имеет размерность [амплитуда/частота]. На каждой конкретнойчастоте амплитуда соответствующей составляющей равна нулю. Сравнивая (1.15) и (1.42), находим, что бесконечно малому интервалу частоты dw соответствует составляющая с бесконечно малой комплексной амплитудой dA(jw):
 (1,43)
(1,43)
Сравнение выражения (1.41) для спектральной характеристики функции u(t), с формулой (1.17) для огибающей комплексного спектра такой же функции, периодически продолжающейся во времени, показывает, что они различаются только множителем:
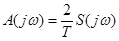 (1.44)
(1.44)
Поэтому по известной спектральной характеристике одиночного импульса легко построить линейчатый спектр их периодической последовательности. Соотношением (1.44) объясняется и тот факт, что для различных представлений спектральной характеристики имеют место формулы, весьма похожие на (1.18) — (1.24).
Как комплексная величина спектральная характеристика может быть записана в виде
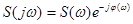 (1.45)
(1.45)
где S(w) = |S(jw)| называется спектральной плотностью амплитуд или спектром непериодического сигнала.
Так как составляющие расположены на всех частотах, то спектр непериодического сигнала является непрерывным или сплошным. Представим спектральную характеристику состоящей из действительной и мнимой частей:
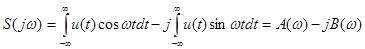 (1.46)
(1.46)
где
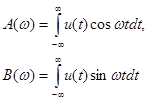 (1.47 - 1-48)
(1.47 - 1-48)
Модуль спектральной характеристики S(w) определяется выражением
 (1.49)
(1.49)
и представляет собой четную функцию частоты.
Для фазы спектральной характеристики S(w) соответственно получаем
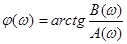 (1.50)
(1.50)
Так как из (1.42) и (1.43) следует, что A(w) — четная функция частоты, а В(w) — нечетная, то функция j(w) относительно частоты нечетна.
Комплексная форма интегрального преобразования Фурье легко приводится к тригонометрической:

Второй член в связи с нечетностью подынтегрального выражения равен нулю. Окончательно имеем
 (1.51)
(1.51)
Преимущество тригонометрической формы записи Фурье-преобразования заключается в возможности некоторого физического толкования с использованием идеализации, не очень далеких от реальности.
Все темы данного раздела:
СИСТЕМА ПЕРЕДАЧИ ИНФОРМАЦИИ
Совокупность средств информационной техники и людей, объединенных для достижения определенных целей или для управления, об
КОЛИЧЕСТВО ИНФОРМАЦИИ
Передача информации инициируется либо самим источником информации, либо осуществляется по запросу. Она диктуется желанием устранить неопределенность относительно последовательности состояний, реали
Передача информации от дискретного источника.
Выясним, насколько будет изменяться неопределенность относительно состояния источника сообщения при получении адресатом элемента сообщения с выхода канала связи. Алфавиты передаваемых и принимаемых
Передача информации от непрерывного источника.
Количество информации, получаемой от непрерывного источника по каналу с помехами, определяется так же, как в случае, рассмотренном выше, но с использованием понятия дифференциальной энтропии.
Свойства фурье-преобразований
Если не использовать комплексную экспоненту, то выражение (2.12)
можно переписать следующим образом:
Умножение и свертка
Добавим теперь два важных соотношения, представляющих теорему умножения:
(2.29)
&
Пространство и время
Кроме связи между пространственными распределениями f(r) и амплитудами дифракции F(u), фурье-преобразование также связывает изменение функции во вр
Точечный источник или точечная апертура
Распределение амплитуды при рассеянии от очень малого источника или при прохождении через очень малую апертуру (или щель) в одном измерении можно описать с помощью функции
Трансляция объекта
Трансляция объекта описывается выражением
(2.37)
здесь и
Функция щели
Функция прохождения для щели шириной a в непрозрачном экране дается выражением:
Другая форма функции щели
Проиллюстрируем использование выражения (2.27). Заметим при этом, что для функции щели, которая была определена в разд. 2.3.4, справедливо выражение:
Прямолинейный край
Для прямолинейного края функция прохождения имеет вид:
Обобщение преобразований Фурье. Преобразования Лапласа
Некоторые колебания не могут быть представлены интегралом (1.21), так как для них не существует или не определена спектральная функция. Это происходит потому, что колебание не удовлетворяет условию
Операция образования величины
часто встречается при расчете радиотехнических процессов и называется сверткой ф
Выражение энергии колебания через его спектральную функцию. Спектральная плотность энергии
Пусть Gs (w) является спектральной функцией колебания напряжения s(t). Тогда удельная энергия колебания (энергия, выделяемая на единичном сопротивлении)
Энергия взаимодействия двух колебаний
Пусть сумма колебаний напряжения s1(t) и s2(t), действует на единичном сопротивлении. Найдем выделяющуюся при этом энергию.
На основании (1.53) и теорем
Соотношение между длительностью колебанияи шириной его спектра. Определения длительности колебания
При рассмотрении спектральной функции любого импульсного колебания можно установить, что чем сосредоточеннее, короче импульс во времени, тем протяженнее его спектральная функция по частоте, т. е. т
Равномерное распределение.
Пусть некоторая случайная величина X может принимать значения, принадлежащие лишь отрезку x2 ³ x ³ x1, причем вероятности попадания в любые внутренние интерва
Гауссово (нормальное) распределение.
В теории случайных сигналов фундаментальное значение имеет гауссова плотность вероятности
(6.9)
Плотность вероятности функции от случайной величины.
Пусть Y — случайная величина, связанная с X однозначной функциональной зависимостью вида у = f(x). Попадание случайной точки х в интервал шириной dx и попадание случайной точки
Функция распределения и плотность вероятности.
Пусть даны случайные величины {Х1 Х2,…,Хn}, образующие n-мерный случайный вектор X. По аналогии, с одномерным случаем функция распределения этого вектора
&
Корреляция.
Предположим, что проведена серия опытов, в результате которых каждый раз наблюдалась двумерная случайная величина {Х1 Х2}. Условимся исход каждого опыта изображать точк
Функциональные преобразования многомерных случайных величин.
Предположим, что составляющие двух случайных векторови
Стационарные случайные процессы
Среди случайных процессов особое место занимают стационарные случайные процессы, имеющие важное значение при рассмотрении большого числа задач. Случайный процесс называется строго
Квазидетерминированные процессы и случайные процессы
Приведенное в настоящей главе описание случайных процессов может быть использовано не только для помех, но и для сигналов в случае, когда параметры сигналов меняются случайным образом на интервале
Предварительные замечания
Высокочастотные колебания, действующие на входе радиоприемного устройства, при достаточно общих предположениях можно представить в виде
Виды помех
Помехи радиоприему имеют весьма разнообразный и сложный характер, что создает определенные трудности при их классификации. Классификацию помех можно проводить по различным признакам, в частности, м
Зависимость уровня помех от частоты
Вразличных диапазонах частот активные помехи проявляют себя неодинаково. Внутриприемные шумы возникают в широком диапазоне частот, однако только на достаточно высоких частотах (при
Законы распределения помех
Рассмотрим применительно к выходу линейной части приемного тракта (УПЧ) модели, определяющие плотности вероятности следующих видов аддитивных помех: флуктуациопных, импульсных, квазиимпульсных и
Случайные процессы как математические модели реальных помех
Реальные помехи, воздействующие на вход радиоприемного устройства, проходя через приемный тракт, включающий линейные и нелинейные элементы, подвергаются существенным преобразованиям. Выбор элемен
Марковские процессы
Удобной идеализацией реальных помех радиоприему являются марковские случайные процессы. Предыдущее рассмотрение показало, что помехи радиоприему могут быть флуктуациоиными и импульсными. Флуктуаци
Флуктуационные помехи
Флуктуационные помехи занимают особое место среди различных видов помех радиоприему. Значительная часть помех, такие, как тепловые шумы в пассивных элементах приемных устройств, шумы в приемной ан
Спектральная плотность флуктуационных помех
Наряду с функцией корреляции для описания случайных процессов широко используется также спектральная плотность g{f), которая характеризует распределение мощности (энергии) помехи или сигна
Белый шум
Флуктуационные помехи, для которых в широкой полосе частот спектральная плотность постоянна, по аналогии с белым светом называют белым шумом. При теоретическом рассмотрении вопросов обнару
ТЕПЛОВЫЕ ШУМЫ
Проведем теперь расчет величины спектральной плотности Su шумовой ЭДС на сопротивлении R, вызванной тепловым движением электронов в проводнике, находящемся при температуре Т. Докажем
ДРОБОВОЙ ШУМ
Шум в лампах в основном создается дробовым эффектом, т. е. беспорядочными флуктуациями анодного тока около среднего значения, которое показывает амперметр постоянного тока. Термин «дробовой» связан
ГЕНЕРАЦИОННО-РЕКОМБИНАЦИОННЫЙ ШУМ
В полупроводниках и в приборах на их основе наблюдается еще один вид шума, создаваемый спонтанными флуктуациями скоростей генерации, рекомбинации и улавливания носителей, что приводит к флуктуациям
ПРИНЦИП ВЫДЕЛЕНИЯ СИГНАЛА ИЗ ШУМА
Методы выделения сигнала из шума основываются на том, что сигнал, несущий информацию, и шумы имеют разные статистические и спектральные характеристики.
Спектр сигнала обычно узкополосный и
СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисных для представления радиотехнических сигналов, особое место занимают гармонические функции. Важность
Ряды Фурье.
Зададим на интервале времени [-T/2, T/2] ортонормированный базис, образованный гармоническими функциями с кратными частотами:
Преобразование Фурье.
Метод рядов Фурье допускает глубокое и плодотворное обобщение, позволяющее получать спектральные характеристики непериодических сигналов. Среди последних наибольший интерес для радиотехники предста
Понятие спектральной плотности сигнала.
Воспользуемся тем, что коэффициенты ряда Фурье образуют комплексно-сопряженные пары:
;
Обратное преобразование Фурье.
Решим обратную задачу спектральной теории сигналов: найдём сигнал по его спектральной плотности, которую будем считать заданной.
Предположим вновь, что непериодический сигнал получается из
Преобразование Лапласа.
Спектральные методы анализа сигналов основаны на том, что исследуемый сигнал представляется в виде суммы неограниченно большого числа элементарных слагаемых, каждое из которых периодически изменяет
Условия существования преобразования Лапласа. Связь между преобразованиями Фурье и Лапласа.
Пусть - некоторый сигнал, определенный при >
Представление отклика линейной цепи в форме интеграла наложения или свертки.
Любой детерминированный сигнал можно представить при помощи единичной ступенчатой или единичной импульсной функции, называемой для краткости единичная ступенька и ед
Дискретное представление сигналов. Теорема Котельникова.
Если в спектре сигнала нет составляющих с частотой выше , то такая частота называется пред
Прохождение сигналов через линейные системы.
Каждое радиотехническое устройство представляет собой систему независимо от своего назначения и уровня сложности, то есть совокупность физических объектов, между которыми существуют определённые вз
Импульсные, переходные и частотные характеристики линейных систем.
Замечательная особенность линейных систем – справедливость принципа суперпозиции – открывает прямой путь к систематическому решению задач о прохождении разнообразных сигналов через
Вход Выход Вход Выход
h(t) H(x)
а) б)
Рисунок 5. Схемы линейных систем: а – линейная колебательная система с сосредоточенными параметрами; б - волновой аналог системы.
Н
ДИАГРАММА НАПРАВЛЕННОСТИ ИЗЛУЧАЮЩЕЙ СИСТЕМЫ
Излучающие системы являются преобразующим звеном между электромагнитными волнами, распространяющимися в свободном пространстве, и электромагнитными волнами, распространяющимися в линии передачи. В
Характеристики диаграмм направленности.
Из диаграммы направленности легко определить направление главного максимума, ширину главного лепестка и относительный уровень главных максимумов.
Относительный уровень боковых максимумов е
Графическое изображение диаграммы направленности.
Одним из наиболее распространенных способов изображения диаграммы направленности антенн является вычерчивание так называемых полярных диаграмм направленности.
Представим ряд векторов, исхо
Двойной физический смысл пространственных частот.
Рассмотрим соотношения, представляющие собой интеграл Фурье для двух пар переменных, и
Фильтрующие свойства свободного пространства
Рассмотрим сначала функцию, являющуюся двухмерной частотной характеристикой свободного пространства:
СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
1.1 Ряды Фурье
1.2 Преобразование Фурье
1.3 Понятие спектральной плотности сигнала
1.4 Обратное преобразование Фурье
1.5 Преобразование Лапласа
1.6 Усло
ДИАГРАММА НАПРАВЛЕННОСТИ ИЗЛУЧАЮЩЕЙ СИСТЕМЫ
2.1 Характеристики диаграмм направленности
2.2 Графическое изображение диаграммы направленности
2.3 Двойной физический смысл пространственных частот
2.4 Фильтрующие свойс
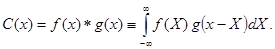


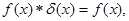
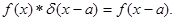

 (1.40)
(1.40)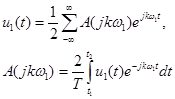
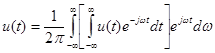
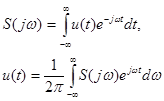 (1.41-1.42)
(1.41-1.42) (1,43)
(1,43)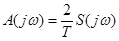 (1.44)
(1.44)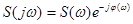 (1.45)
(1.45)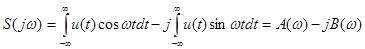 (1.46)
(1.46)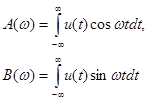 (1.47 - 1-48)
(1.47 - 1-48) (1.49)
(1.49)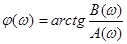 (1.50)
(1.50)
 (1.51)
(1.51)






Новости и инфо для студентов