рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Информатика
- /
- РАЗДЕЛ 1.МЕСТО И РОЛЬ ПРОЦЕССОВ ПОДГОТОВКИ И ПРИНЯТИЯ РЕШЕНИЙ В ОБЩЕЙ ТЕХНОЛОГИИ УПРАВЛЕНИЯ СЛОЖНЫМИ ОРГАНИЗАЦИОННО-ТЕХНИЧЕСКИМИ СИСТЕМАМИ (СОТС
Реферат Курсовая Конспект
РАЗДЕЛ 1.МЕСТО И РОЛЬ ПРОЦЕССОВ ПОДГОТОВКИ И ПРИНЯТИЯ РЕШЕНИЙ В ОБЩЕЙ ТЕХНОЛОГИИ УПРАВЛЕНИЯ СЛОЖНЫМИ ОРГАНИЗАЦИОННО-ТЕХНИЧЕСКИМИ СИСТЕМАМИ (СОТС
РАЗДЕЛ 1.МЕСТО И РОЛЬ ПРОЦЕССОВ ПОДГОТОВКИ И ПРИНЯТИЯ РЕШЕНИЙ В ОБЩЕЙ ТЕХНОЛОГИИ УПРАВЛЕНИЯ СЛОЖНЫМИ ОРГАНИЗАЦИОННО-ТЕХНИЧЕСКИМИ СИСТЕМАМИ (СОТС - раздел Информатика, Раздел 1.Место И Роль Процессов Подготовки И...
РАЗДЕЛ 1.МЕСТО И РОЛЬ ПРОЦЕССОВ ПОДГОТОВКИ И ПРИНЯТИЯ РЕШЕНИЙ В ОБЩЕЙ ТЕХНОЛОГИИ УПРАВЛЕНИЯ СЛОЖНЫМИ ОРГАНИЗАЦИОННО-ТЕХНИЧЕСКИМИ СИСТЕМАМИ (СОТС).
Общая характеристика задач подготовки и принятия решений в СОТС.
Среди системных направлений науки ведущее место занимают системный анализ, системотехника, теория управления, инженерия знаний, исследование… Исследование операций, как научная дисциплина, получила свое существенное… Выдающемуся советскому ученому, академику, лауреату Ленинской и Нобелевской премий Л.В.Канторовичу принадлежит…Концептуальная модель принятия решений
Анализ многочисленных публикаций по различным аспектам проблемы выбора показывает, что в настоящее время наметилась прогрессивная тенденция к… Интегрированный подход к использованию достижений, полученных в рамках… Отношение предпочтения следует считать центральным понятием теории выбора. Широкое привлечение аксиоматики бинарных…Обобщенная структура современных интегрированных систем поддержки принятия решений
Рис.1.3.1. Функциональная схема интегрированной системы поддержки принятия решений по управлению структурной динамикой СОТС.Постановка задачи линейного программирования
Пусть имеется т видов ресурсов, каждый i-й ресурс в количестве bi (i=1...m). Эти ресурсы нужно использовать для п видов продукции. Для выпуска… В реальных задачах суммарное количество основных xj (j = 1...n) и… Цель задачи распределения ресурсов устанавливается какой-либо одной из двух взаимоисключающих постановок:Экономическая интерпретация задачи линейного программирования
Из таб.2.1 видно, что для выпуска единицы продукции, например вида П2, требуется две единицы трудовых ресурсов, П3 – четыре единицы материальных… Таблица 2.2.1 Ресурсы (i) Вид продукции ( j) Запас … На основании исходных данных требуется составить математическую модель для определения плана выпуска продукции.Анализ существования решений в задаче линейного программирования
В общую постановку задачи оптимизации входят неравенства вида (i =1...т), где п – число неизвестных; т – число неравенств. Если в каждое неравенство… В этой системе общее число неизвестных N = n+m, где п – число основных… Возможны три варианта соотношения величин N и т.Графический метод решения задач линейного программирования
Линейное уравнение с двумя переменными может быть записано a1x1+a2x2 =b. Чтобы построить это уравнение, найдём точки пересечения с осями координат.… Разделим теперь левую и правую части уравнения на b и перепишем уравнение ,… Теперь вспомним неравенства. Если линейное уравнение с двумя переменных 2х1+х2=2 может быть представлено прямой на…Двойственные задачи линейного программирования
ДЗ по отношению к прямой составляют согласно правилам: 1) ЦФ ПЗ задаётся на max, тогда ЦФ ДЗ – на min, и наоборот; 2) матрица , составленная из коэффициентов вGt; 10;
2 · 5,75 + 1,25 = 14;
5,75 + 5 · 1,25 = 12.
Первое ограничение выполняется как строгое неравенство, т.е. двойственная оценка всех ресурсов на производство единицы изделия А выше цены этого изделия и, следовательно, выпускать его невыгодно. Его производство и не предусмотрено оптимальным планом ПЗ.
При одновременном изменении ресурсов всех видов на величину Dbi (i=1...m) можно оценить их суммарное влияние на значение ЦФ (при условии неизменности двойственных оценок в новой ДЗ относительно оценок в первоначальной ДЗ):
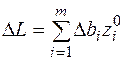 ,
,
где Dbi – величина возможного (при сохранении оптимального плана первоначальной ДЗ) изменения (увеличения или уменьшения) ресурса i-го вида.
Анализ решений задач линейного программирования.
Решением этой задачи являются следующие значения переменных и (см. рис. 2.6.1): . а) б)Таблица 2.6.1.
| Характеристика | Вид продукции | Располагаемый ресурс | |
| П1 | П2 | ||
| Резервы: | |||
| трудовые | |||
| материальные | |||
| финансовые | |||
| Выпуск | — | ||
| Прибыль | 8,5 | — | |
| План | 
| 
| — |
Для каждой приведенной целевой функции аналогично тому, как это делалось для  , можно построить линию целевой функции и определить вершину в которой целевая функция будет иметь оптимальное значение. Результаты решения задачи по пяти целевым функциям сведены в табл. 2.6.2, из анализа которой можно сделать следующий вывод: координаты каждой вершины могут быть оптимальным решением задачи в некотором принятом смысле. Так, вершина С дает максимальный суммарный выпуск, вершины А — максимальный выпуск продукции П2и т.д.
, можно построить линию целевой функции и определить вершину в которой целевая функция будет иметь оптимальное значение. Результаты решения задачи по пяти целевым функциям сведены в табл. 2.6.2, из анализа которой можно сделать следующий вывод: координаты каждой вершины могут быть оптимальным решением задачи в некотором принятом смысле. Так, вершина С дает максимальный суммарный выпуск, вершины А — максимальный выпуск продукции П2и т.д.
Таблица 2.6.2.
| Целевая функция | Вершина | 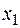
| 
| 
| Прибыль | Используемый ресурс |
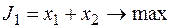
| С | 1,5 | 5,5 | 28,75 | ||
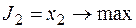
| A | 3,5 | 3,5 | 29,75 | ||
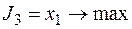
| D | 4,5 | 4,5 | |||

| B | 33,5 | ||||
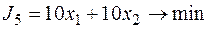
| F |
Если перед нами стоит задача минимизировать используемые ресурсы, то очевидно, что при отсутствии требований на заданную номенклатуру ничего не надо выпускать.
Пользоваться таблицами типа 2.6.2 при анализе различных вариантов планов, несомненно, полезно. При этом окончательный выбор варианта оптимального плана должен делать не специалист по математическим методам, а руководитель, т.е. лицо, принимающее решение.
Рассмотрим далее, как влияет на оптимальное решение введение дополнительных ограничений. Пусть дана задача, которая графически представлена на рис. 2.6.2, а. Принимаем, что при максимизации оптимальное решение находится в вершине А и имеет значения 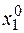 ,
, 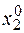 ,
,  . Рассмотрим, как влияют на оптимальное решение дополнительные ограничения, например, применительно к
. Рассмотрим, как влияют на оптимальное решение дополнительные ограничения, например, применительно к 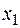 .
.
Таблица 2.6.3.
| См. рис. 2.6.2 | 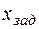
| 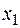
| 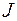
|
| б | 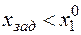
| 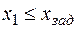
| 
|
| в | 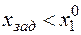
| 
| 
|
| г | 
| 
| 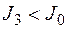
|
| д | 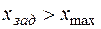
| 
| Нет |
Из рис. 2.6.2 и данных табл. 2.6.3 видно следующее: дополнительное ограничение ухудшило целевую функцию (рис. 2.6.2, б); оптимальное решение не изменилось (рис. 2.6.2, в); оптимальное решение ухудшилось (рис. 2.6.2, г); характерно появление несовместности (рис. 2.6.2, д), которое привело к тому, что задача вообще не имеет решения.
Выводы:
1. Если оптимальным решением являются координаты вершины ОДР, то это значит, что сколько вершин имеет ОДР, столько оптимальных решений может иметь задача.
2. Поскольку чем больше ограничений, тем больше вершин, то, следовательно, чем больше ограничений, тем больше оптимальных решений.
3. Дополнительные ограничения в задачах ЛП не улучшаются ранее полученных оптимальных решений.
2.7. Содержательная и формальная постановка
транспортной задачи.
Транспортная модель является частным случаем общей сетевой модели оптимизации, интерес к которым связан с тем, что в рамках терминологии сетевых (графовых) моделей описываются многие задачи принятия решений, связанные с управлением системами различной природы. Особенности математической структуры сетевых моделей позволяют строить эффективные вычислительные алгоритмы решения таких задач, и именно этот фактор позволяет выделить транспортные задачи в самостоятельный класс специальных задач, изучение которых имеет важные практические приложения в различных областях деятельности.
Представим транспортную модель в следующем виде. Имеется:
- множество поставщиков A = {Ai, i = 1,…, m};
- множество потребителей B = {Bj, j = 1,…, n}.
Каждому поставщику соответствует объем имеющегося у него ресурса ai, а каждому потребителю сопоставляется объем необходимого для него ресурса bj. Предполагается, что каждый поставщик соединен с каждым потребителем, т.е. множество дуг такой сети E = A ´ B. Задана функция c: E ® R1, характеризующая некоторое качество (время, стоимость, и т.п.) перевозки по дуге
eij = (Ai, Bj) Î E
В этом случае математической конструкцией, описывающей решение, может являться вектор
x = (x11, x12,....,x1n, x21,....,x2n,...., xmn)т = ║xij║,
компоненты которого xij характеризуют объем перевозок от поставщика Ai к потребителю Bj. Ограничения накладываются на объем продукции, вывозимой от i-го поставщика, и количество продукции, которую необходимо завести
j-му потребителю. Целевая функция характеризует суммарные расходы на все такие перевозки.
Тогда математическая модель классической транспортной задачи имеет вид:
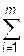
 cij xij ® min (1)
cij xij ® min (1)
при ограничениях
 xij £ ai, i = 1,…, m, (2)
xij £ ai, i = 1,…, m, (2)
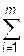 xij ³ bj, j = 1,…, n, (3)
xij ³ bj, j = 1,…, n, (3)
xij ³ 0, i = 1,…, m, j = 1,…,n. (4)
В ситуациях, когда имеется равенство суммарного ресурса у всех поставщиков и суммарных потребностей всех потребителей,
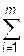 ai =
ai = bj , (5)
bj , (5)
неравенства в ограничениях транспортной модели приобретают вид равенств.
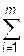
 cij xij ® min (6)
cij xij ® min (6)
 xij = ai, i = 1,…, m, (7)
xij = ai, i = 1,…, m, (7)
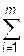 xij = bi, j = 1,…, n, (8)
xij = bi, j = 1,…, n, (8)
xij ³ 0, i = 1,…, m, j = 1,…,n. (9)
Такая задача называется стандартной (закрытой) транспортной задачей. Следует отметить, что произвольная транспортная задача может быть сведена к стандартной путем введения фиктивных поставщиков (потребителей), объем ресурсов (потребностей) которых равен разности левой и правой части в ограничениях (2) (или (3)).
Транспортная задача (6)–(9) описывается линейными ограничениями и линейной целевой функцией, следовательно, для ее решения могут использоваться стандартные методы линейного программирования (симплекс-метод, например). Размерность такой задачи равна (m+n)´(mn). Однако для решения транспортных задач был разработан специализированный алгоритм (метод потенциалов), учитывающий особенности данной задачи. Рассмотрим, в чем состоят эти особенности.
2.8. Содержательная и формальная постановка
задачи о назначениях.
Частным случаем классической транспортной задачи (1)–(4) раздела 2.7 является задача о назначениях, которая помимо того, что сама имеет важное прикладное значение, часто используется, как вспомогательная при решении дискретных оптимизационных задач различного рода. Практическая суть задачи, из которой и возникло ее название, заключается в том, что имеется (n) должностей, на которые могут быть назначены (n) кандидатов, причем назначение некоторого i–го кандидата на j-ю должность связано с расходами равными cij. Необходимо так распределить кандидатов на должности, чтобы суммарные расходы были минимальны.
В этих условиях решение (распределение кандидатов) можно описать вектором x с компонентами xij, которые принимают значение 1 или 0 в зависимости от того, назначается i–ый кандидат на j–ю должность, или нет. Математическая модель такой задачи имеет вид

 cij xij ® min (1)
cij xij ® min (1)
при ограничениях
 xij = 1, i = 1,…, n, (2)
xij = 1, i = 1,…, n, (2)
 xij = 1, j = 1,…, n, (3)
xij = 1, j = 1,…, n, (3)
xij Î {0, 1}, i = 1,…, n, j = 1,…,n. (4)
Такая задача относится к классу задач линейного дискретного (целочисленного, булевого) программирования. В силу абсолютной унимодулярности матрицы условий такой задачи многогранник условий имеет только целочисленные вершины, поэтому решение такой задачи может быть получено на основе симплекс-метода. Так как задача о назначениях является частным случаем транспортной задачи, то она может быть решена и с использованием метода потенциалов.
Раздел 3.ПОСТАНОВКА И МЕТОДЫ РЕШЕНИЯ ДЕТЕРМИНРОВАННЫХ ЗАДАЧ ВЫБОРА С НЕЛИНЕЙНОЙ ЦЕЛЕВОЙ ФУКНЦИЕЙ И НЕЛИНЕЙНЫМИ ОГРАНИЧЕНИЯМИ
3.1. Особенности задач выбора с нелинейной целевой функцией и нелинейными ограничениями (задач нелинейного
программирования (НЛП))
В задачах ЛП полагалось, что себестоимость, цена и другие показатели, оценивающие эффективность организации производства не зависят от объема производства (вектор 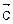 не зависит от
не зависит от 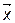 ). Однако, в общем случае, это не так. Так, например, на практике себестоимость единицы продукции снижается при увеличении объема производства (вектор
). Однако, в общем случае, это не так. Так, например, на практике себестоимость единицы продукции снижается при увеличении объема производства (вектор  ). Для учета данных ситуаций вводят новый класс моделей исследования операций.
). Для учета данных ситуаций вводят новый класс моделей исследования операций.
Определение 1. Задача выбора, в которой зависимости между переменными в целевой функции и/или в ограничениях являются нелинейными, называется задачей нелинейного программирования.
В общем случае задача нелинейного (математического) программирования имеет следующий вид:
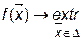
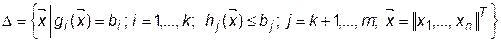
В зависимости от свойств, которыми обладают функции  ,
,  ,
, 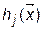 различают следующие классы задач нелинейного программирования:
различают следующие классы задач нелинейного программирования:
Определение 2. Множество (область) 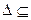 Rn называется выпуклым, если с каждыми двумя точками (альтернативами)
Rn называется выпуклым, если с каждыми двумя точками (альтернативами)  и
и 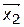 , ему принадлежащими, оно включает весь отрезок, соединяющий данные точки, т. е. выполняется соотношение
, ему принадлежащими, оно включает весь отрезок, соединяющий данные точки, т. е. выполняется соотношение
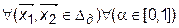
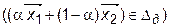
 — выпуклое по определению.
— выпуклое по определению.
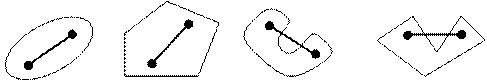
Определение 3. Функция 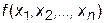 , заданная на выпуклом множестве
, заданная на выпуклом множестве  , называется выпуклой, если для любых двух точек
, называется выпуклой, если для любых двух точек  и
и 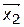 из
из  и любого
и любого  выполняется соотношение
выполняется соотношение
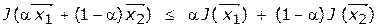


Согласно определению признака экстремума функция f(x) имеет максимум (минимум) в точке х*, если в достаточной близости от этой точки всем значениям х соответствуют значения f(x) меньшие (большие), чем f(x*). Для случая максимума это показано на рис. 3.1.1.
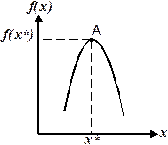 Рис. 3.1.1
Рис. 3.1.1
|

Рис. 3.1.2
Максимум и минимум функции объединяются понятием экстремум, который может быть как локальным, так и глобальным. На рис. 3.1.2 функция f(x) принимает максимальные значения в вершинах В и D. При этом B > D. В таком случае говорят, что точка В является глобальным максимумом, а точка D — локальным. Аналогично функция f(x) принимает минимальные значения в точках А, С, Е, причем С < A < E. В этом случае С будет глобальным минимумом, а А и Е — локальными минимумами. Из приведенных примеров видно, что глобальным максимумом (минимумом) называют такой максимум (минимум), который больше (меньше) всех остальных.
 Рис. 3.1.3
Рис. 3.1.3
|
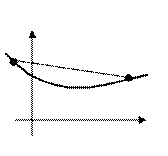
Достаточно часто при введении граничных условий типа х £ b, показанных на рис. 3.1.3, наибольшее значение функции находится на границе в точке х = b. При этом величина f(b) не удовлетворяет приведенному выше признаку экстремума.
В таких случаях говорят, что в точке х = b находится оптимум функции f(b) = B.
Наибольшее или наименьшее значение функции без учета того, где находится такое значение, — внутри заданного интервала или на его границе — называют оптимумом. Оптимум — более широкое понятие, чем экстремум. Если экстремум есть не у всех функций, то в практических задачах оптимум, как правило, есть всегда. Так же как и экстремумы, оптимумы могут быть локальными и глобальными.
Существующие методы дают возможность находить только локальные оптимумы. Если же есть подозрение, что в заданном интервале аj £ xj £ bj целевая функция f(xj) может иметь несколько оптимумов, то этот интервал следует разбить на n интервалов, в каждом интервале определить свои локальные оптимумы, а затем из всех локальных оптимумов выбрать глобальный. В таком случае задача нахождения глобального оптимума сводится к решению ряда задач, в которых ищется локальный оптимум.
В дальнейшем мы будем рассматривать нахождение только локального оптимума. Следует отметить, что в подавляющем большинстве практических экономических и технических задач оптимизации существует только один оптимум. Задачи нелинейной оптимизации с точки зрения методов решения делятся на два класса:
r задачи безусловной оптимизации;
r задачи условной оптимизации.
Особенности задач НЛП:
1. По сравнению с рассмотренными ранее задачами линейного программирования, в которых оптимальное решение соответствует некоторым крайним точкам (вершинам) выпуклого многогранника, в задачах нелинейного программирования оптимальное решение может соответствовать произвольной точке области D. В этих задачах решение может находиться как в точке, расположенной на границе допустимой области, так и в точке, расположенной внутри области, что определяется свойствами целевой и ограничивающих функций.
2. Многосвязность допустимой области и многоэкстремальность задачи. В задачах нелинейного программирования при произвольных ограничениях множество допустимых решений D может быть многосвязным, т.е. представлять собой объединение непересекающихся подмножеств. Решение в каждой такой области следует искать независимо от других, и выбирать из них наилучшее, однако установление факта многосвязности D, как правило, достаточно трудоемко.
Нахождение оптимума произвольной функции в допустимой области D, даже если она задается линейными ограничениями, равно как и нахождение оптимума даже линейной функции на невыпуклом множестве D, может привести к тому, что в исходной оптимизационной задаче будет существовать несколько локальных экстремумов, т.е. другими словами такая задача будет многоэкстремальна. Существуют значительные трудности в определении локальных экстремумов, число которых в общем случае может быть достаточно велико.
3. Так как целевая функция и множество допустимых альтернатив в задачах нелинейного программирования описываются произвольными нелинейными функциями, в ряде приложений эти функции могут быть разрывными или недифференцируемыми. Это создает дополнительные трудности в решении таких задач и требует разработки специфических методов нахождения оптимальных решений.
Обобщенный алгоритм решения задач НЛП
xk+1 = xk + hk r(xk), k = 0,1,.... (1) Здесь k - номер итерации;Метод приведенной безусловной оптимизации
Методы данной группы строятся на основе использования концепции "погружения", когда исходная задача нелинейного программирования с ограничениями приводится к задаче оптимизации некоторой функции F(x) в условиях отсутствия ограничений, и далее используются методы безусловной оптимизации. В качестве таких функций наиболее часто используются функции Лагранжа и штрафные функции.
Аналитические методы решения задач НЛП
Шаг 1. Формирование функции Лагранжа (переход от задачи на условный экстремум к задаче не безусловный экстремум). — неопределенные множители Лагранжа.Численные методы решения задач НЛП
xk+1 = xk + hk ÑF(xk), k = 0,1,.... (1) Алгоритмы, построенные на основе градиентного метода, носят итерационный… 0. Исходное состояние. Задается начальная точка xo, некоторое малое e ≥ 0; k = 0.Постоянный шаг.
F(xk+1) = F(xk + hkÑF(xk)) > F(xk). Пусть F(x) дифференцируема в окрестности точки xk. ТогдаНаискорейший подъем.
hk = max F(xk+hÑF(xk)) (3) h≥0 Последнее выражение представляет собой задачу одномерной оптимизации.Функции Лагранжа
L(x, m) = f(x) + mт(b - j(x)) = f(x) + mi (bi - j i(x)), где mi ≥ 0, i=1,...,m - множители Лагранжа. В соответствии с теоремой Куна-Таккера необходимым и достаточным условием оптимальности является то, что точка (x*,m*)…Штрафные функции
Fk(x, m) = f(x) - Sk(x, mk), k = 1,2,3,.... Здесь Sk(x,mk), k = 1,2,3,... - штрафные функции, задаваемые таким образом,… Различают три основных способа формирования штрафных функций:Методы прямой условной оптимизации
Итак, пусть решается задача нелинейного программирования f(x) ® max, (4) xÎDМетод условного градиента
x = xk + r(xk), или отсюда r(xk) = x - xk. С другой стороны из определения (2.2) дифференцируемости функции в точке xk … f(x) = f(xk) + Ñтf(xk)(x - xk) + o(║x - xk║)Постановка задачи целочисленного программирования
Первые упоминания о линейных уравнениях возникли ещё за несколько веков до нашей эры. В Древней Греции Диофант (II-III в.) формулирует уравнения, в которых искомые… Для уравнения с двумя неизвестными: а1х1+а2х2=0, где а1, а2 – целые, решение будет х1=–(а2/а1)х2. Например,Таблица 3.4.1.
| Точка (рис. 3.4.1) | 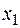
| 
| 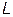
| Решение |
| A | 2,8 | 4,3 | 5,14 | Непрерывное |
| B | — | Недопустимое | ||
| С | 3,9 | Допустимое | ||
| D | 4,6 | Оптимальное |
На основании рассмотренного примера можно сделать следующие выводы: округление оптимальных значений переменных в непрерывном решении даже в меньшую сторону может привести к недопустимому решению; оптимальным решением целочисленной задачи может оказаться такое, в котором значения переменных не являются ближайшими к оптимальному решению непрерывной задачи.
Таким образом, решение целочисленных задач — процедура весьма трудоемкая. В связи с этим по возможности лучше не накладывать требований целочисленности переменных. Подобная возможность может определяться как из содержательной постановки задачи, так и в том случае, когда ожидаемые значения целочисленных переменных не меньше десяти. В ряде случаев рассматриваемую задачу упрощенно можно решать следующим образом: решать непрерывную задачу; округлять переменные; проверять допустимость округленного решения; если округленное решение является допустимым, принять его в качестве решения. При этом надо отдавать себе отчет в том, что принятое решение, которое является допустимым, нет никаких оснований считать оптимальным.
Для нахождения оптимального решения целочисленных задач применяют специальные методы, в которых учитывается, что число возможных решений любой целочисленной задачи является конечным. Так, в задаче с переменными 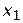 и
и 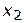 , удовлятворяющими граничным условия
, удовлятворяющими граничным условия 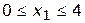 ,
,  , число возможных решений
, число возможных решений 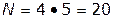 . Следовательно, можно рассмотреть все возможные сочетания
. Следовательно, можно рассмотреть все возможные сочетания 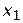 и
и 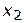 , проверить, удовлетворяют ли они ограничениям, и из числа удовлетворяющих ограничениям, т. е. допустимых, выбрать наилучшее в смысле принятой целевой функции.
, проверить, удовлетворяют ли они ограничениям, и из числа удовлетворяющих ограничениям, т. е. допустимых, выбрать наилучшее в смысле принятой целевой функции.
Такой метод называют методом полного перебора. Его трудоемкость с ростом числа переменных и расширением области граничных условий значительно возрастает. Поэтому для реальных задач он неприменим.
Основные этапы решения задачи целочисленного программирования (ЗЦП) методом ветвей и границ
Шаг 1. Исходная ЗЦП решается как задача линейного программирования (ЗЛП) (снимаем ограничения вида (г)). При этом за «рекорд» в ЗЦП принимают… Шаг 2. Если все переменные приняли целочисленные значения, то получено… (1),Постановка задачи бивалентного (булева) программирования
Перейдем теперь к частному случаю задач целочисленного программирования. В этом частном случае искомая переменная в результате решения может… С помощью булевых переменных можно решать самые различные по содержанию… Задача выбора вариантов. Примем, что для получения результатов в виде прибыли необходимо два вида ресурсов:…Таблица 3.7.1.
| Характеристика | Наличие | ||||
| Прибыль | — | ||||
| Ресурсы: | |||||
| материальные | |||||
| трудовые |
Количество расходуемого ресурса и получаемая прибыль для каждого варианта приведена в табл. 3.7.1. Требуется выбрать, какие варианты принять для реализации при условии, чтобы общее число принятых вариантов не превышало трех, т. е.  . Для составления модели принимаем, что
. Для составления модели принимаем, что  –му варианту будет соответствовать
–му варианту будет соответствовать  . При этом
. При этом
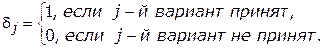
| (1) |
Математическая модель задачи будет иметь вид:
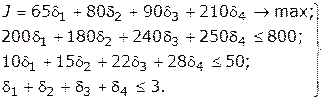
| (2) |
Последняя строка системы (2) обеспечивает удовлетворение требования, чтобы общее число принятых вариантов не превышало трех. Результаты решения задачи приведены в первом столбце табл. 3.7.2, из которого видно, что наибольшая прибыль  будет получена в том случае, если будут приняты третий и четвертый варианты. С помощью булевых переменных можно накладывать дополнительные различные логические условия связи между вариантами.
будет получена в том случае, если будут приняты третий и четвертый варианты. С помощью булевых переменных можно накладывать дополнительные различные логические условия связи между вариантами.
Таблица 3.7.2.
| Дополнительное условие | Нет | 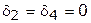
| 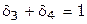
|
| Прибыль | |||
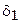
| |||
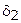
| |||
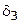
| |||

|
Например, требуется, чтобы четвертый вариант был принят только в том случае, если принят второй. Если же второй вариант не принят, то и четвертый не должен быть принят. Это условие можно записать так:  , или в форме записи ограничений
, или в форме записи ограничений
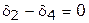
| (3) |
Результат решения задачи с учетом этого дополнительного условия приведен также в табл. 3.7.2.
Рассмотрим еще один вариант дополнительных условий. Допустим, нам надо, чтобы был принят либо третий вариант, либо четвертый. Это условие записывается так:
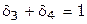
| (4) |
Результат решения задачи с этим дополнительным условием приведен также в табл. 3.7.2.
Сравнивая значения прибыли в оптимальном решении  с полученными значениями прибыли при выполнении дополнительных условий, можно сделать вывод, что дополнительные условия, как всегда, привели к снижению прибыли.
с полученными значениями прибыли при выполнении дополнительных условий, можно сделать вывод, что дополнительные условия, как всегда, привели к снижению прибыли.
Переходя от нашего примера, описываемого системой (2) с дополнительными условиями (3) и (4), к общему случаю, задачу выбора вариантов можно записать так:
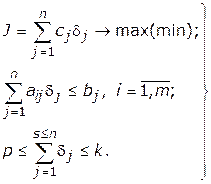
| (4) |
В этой системе ограничение  может учитывать самые разнообразные условия. Рассмотрим некоторые из них. Если накладывается требование «должен», то в ограничениях ставится знак равенства, если «может» — знак неравенства.
может учитывать самые разнообразные условия. Рассмотрим некоторые из них. Если накладывается требование «должен», то в ограничениях ставится знак равенства, если «может» — знак неравенства.
Так, если число принимаемых вариантов в нашем примере должно было бы быть равным 3, то надо было записать
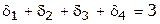
Если накладывается требование «и», то условие записывается следующим образом:
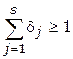 .
.
Например, если могут быть приняты и первый и третий варианты, то 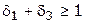 . Если для вариантов накладывается требование «или», то это условие записывается так:
. Если для вариантов накладывается требование «или», то это условие записывается так:

т. е., если из двух вариантов надо принять только один, то должно быть выполнено условие  .
.
Значит, если обозначить 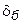 — соответствует «быть»,
— соответствует «быть»,  — «не быть», то вопрос «быть или не быть» может быть записан следующим образом:
— «не быть», то вопрос «быть или не быть» может быть записан следующим образом:
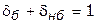
В этом случае есть два допустимых решения:  ;
; 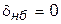 — означает «быть»;
— означает «быть»;  ;
; 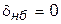 — означает «не быть». Так как целевая функция не сформулирована, то дать оптимальный ответ на этот извечный вопрос невозможно. Чтобы принять решение, необходимо знать, чего мы хотим.
— означает «не быть». Так как целевая функция не сформулирована, то дать оптимальный ответ на этот извечный вопрос невозможно. Чтобы принять решение, необходимо знать, чего мы хотим.
Эвристический метод решения задачи булева программирования.
Существует два метода решения задач с булевыми переменными. Во-первых, их можно решать как обычные задачи целочисленного программирования,… Вторым методом является метод сплошного перебора. Посмотрим его на таком примере. Пусть требуется решить систему: …Таблица 3.8.1.
| Вариант | 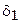
| 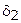
| 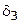
| (а) | (б) | (в) | (г) | 
|
| –2 | ||||||||
| –1 | ||||||||
| Требование | £2 | £4 | £3 | £6 | max |
3. Вычеркнуть те варианты, в которых не удовлетворяется хотя бы одно ограничение. В примере ограничение (а) не удовлетворяется в четвертом варианте; ограничение (2) — в четвертом, седьмом и восьмом, которые таким образом, вычеркиваются как приводящие к недопустимым решениям.
4. Из оставшихся вариантов принимается тот, в котором целевая функция приобретает максимальное значение. В примере оно равно 8; при этом оптимальный вариант — шестой, в котором 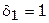 ;
; 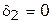 ;
;  ;
;  .
.
Из рассмотренного примера видно, что в данном случае всего вариантов будет 23=8 и для каждого варианта надо вычислить четыре ограничения и целевую функцию, т. е. выполнить 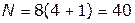 вычислительных операций. В общем случае число вычислительных процедур при полном переборе
вычислительных операций. В общем случае число вычислительных процедур при полном переборе
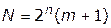 ,
,
где  — число переменных;
— число переменных; 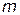 — число ограничений. Число вычислительных процедур для некоторых значений и приведено в табл. 3.8.2, из которой видно, как резко увеличивается число вариантов, которые надо вычислить при увеличении размерности решаемой задачи.
— число ограничений. Число вычислительных процедур для некоторых значений и приведено в табл. 3.8.2, из которой видно, как резко увеличивается число вариантов, которые надо вычислить при увеличении размерности решаемой задачи.
Таблица 3.8.2.

| 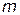
| ||
Для сокращения трудоемкости, необходимой при полном переборе, были предложены различные методы. Рассмотрим один из них, в котором работу производят в такой последовательности.
1. Принять некоторые значения 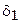 ,
, 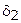 ,
, 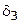 . Для конкретности изложения принимает
. Для конкретности изложения принимает 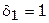 ;
; 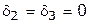 .
.
2. Определить значение целевой функции при таком наборе переменных
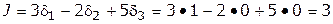
Значит, при принятом наборе переменных целевая функция  . Поэтому не будем рассматривать варианты, в которых целевая функция принимает меньшие значения. Для этого вводим дополнительное ограничение
. Поэтому не будем рассматривать варианты, в которых целевая функция принимает меньшие значения. Для этого вводим дополнительное ограничение
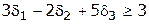 , ,
| (Ф) |
которые будем называть фильтром.
3. Составить табл. 3.8.3.
4. Проверить для каждого варианта выполнение ограничений. Вычисление для каждого варианта прекращать в том случае, если будет не выполнено хотя бы одно ограничение, включая фильтр. Если вычисление прекращается и величины не определены, то в клетках табл. 3.8.3 ставится прочерк. Введение фильтрующего ограничения (Ф) привело в тому, что в табл. 3.8.3 вычислены 24 величины вместо 40 при полном переборе, что составило 60%.
Таблица 3.8.3.
| Номер варианта | 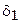
| 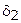
| 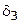
| 
| (а) | (б) | (в) | (г) |
| — | — | — | — | |||||
| –2 | — | — | — | — | ||||
| — | — | — | — | |||||
| –1 | ||||||||
| — | — | |||||||
| — | — | |||||||
| Требование | ³3 | £2 | £4 | £3 | £6 |
Число вычислений можно еще уменьшить, если фильтр иметь не постоянный для всего цикла вычислений, а изменяющийся. Напомним, что в качестве фильтра было принято значение целевой функции при некотором наборе переменных, т. е. некоторое допустимое решение. Если в ходе вычислений при каком-либо наборе переменных значение целевой функции окажется лучше, чем у фильтра, то это новое лучшее допустимое решение следует принять для следующих вычислений в качестве нового фильтра. Такой фильтр называют адаптивным. Покажем, как вести вычисления с помощью адаптивного фильтра. Из табл. 3.8.3 видно, что в пятом варианте 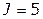 . Поэтому для дальнейших вычислений в качестве фильтрующего ограничения принимаем ограничение
. Поэтому для дальнейших вычислений в качестве фильтрующего ограничения принимаем ограничение
 . .
| (Ф-1) |
Однако для следующего варианта целевая функция будет уже больше и равна .
Значит, в качестве фильтрующего принимаем опять новое ограничение
 . .
| (Ф-2) |
Для седьмого и восьмого вариантов, для которых целевая функция не удовлетворяет требованиям фильтра (Ф-2), значения ограничений не вычисляем. Значит, благодаря трехкратному введению фильтров мы сократили число величин, для которых надо производить вычисления, еще на 4. Итого надо выполнить 20 вычислений вместо 40 при полном переборе, т. е. в 2 раза меньше.
Есть методы, с помощью которых наибольшее значение фильтра можно получить на первых вариантах расчета. Тогда сокращение трудоемкости при вычислениях будет еще более значительным. Такой современный метод называют методом Баллаша с фильтром.
Раздел 4. МЕТОДЫ И МОДЕЛИ МНОГОКРИТЕРИАЛЬНОГО ВЫБОРА
Структура выбора со многими отношениями предпочтения
Характерные особенности задач многокритериального выбора
Реальные задачи выбора, возникающие на практике, чрезвычайно разнообразны, но всех их объединяет общая схема поиска решения, суть которой состоит в… Для поиска указанных альтернатив в задачах выбора необходимо задать… Можно указать на 4 основных вида задач выбора, при решении которых необходимо использовать многокритериальный подход.…Уточненное описание структуры выбора с многими отношениями предпочтения. Общая постановка задач векторной оптимизации
где — множество допустимых альтернатив; — множество исходных отношений предпочтения; — множество правил согласований отношений предпочтения.Множество эффективных альтернатив и его основные свойства
Принцип В.Парето в задачах многокритериального выбора
В п. 4.1 было установлено, что для корректного решения задач многокритериального выбора необходимо в исходную постановку задачи (4.1)‑(4.2)… Определение 4.1. Альтернативы удовлетворяют отношению доминирования по Парето… Данное определение можно задать в виде единого соотношения вида:Основные свойства множества Парето
Рассмотрим основные свойства множества Парето (множества и соответственно ). При этом, как и ранее будем предполагать, что все целевые функции… Свойство № 1. Никакие альтернативы, принадлежащие множеству допустимых… Свойство № 2. При переходе от одной точки (альтернативы) множества Парето к другой точке множества Парето происходит…Методы построения множества Парето
Приведенные в п.4.2.2 свойства множества Парето могут быть использованы для построения (исследования) данного множества (либо его подмножеств) или… В этом случае задача выделения всех эффективных решений сводится к… К настоящему времени наиболее конструктивные результаты, связанные с построением множества Парето, получены для…Классификация современных методов решения задач многокритериального выбора
После выделения множества Парето выбор наиболее предпочтительных альтернатив (с точки зрения ЛПР) уже осуществляется из указанного множества. Однако данная задача, как уже подчеркивалось ранее в п.4.1, является некорректной и в этой ситуации для поиска наилучшей альтернативы необходимо получение дополнительной информации, на основе которой формируется соответствующее результирующее отношение предпочтения (правило согласования).
К настоящему времени разработано большое разнообразие методов решения задач многокритериального выбора. При классификации данных методов могут быть предложены различные принципы и признаки. Так, например, в работах предлагается различать классы: априорных, апостериорных и адаптивныхметодов и моделей многокритериальной оптимизации.
В априорных методах требуемой дополнительной информацией является непосредственно принцип оптимальности, представленной в явном виде либо формульным соотношением между частными свойствами (оценками свойств) альтернативы, либо таким понятием лучшего решения, определение которого становится возможным на основе бинарного отношения доминирования на множестве оценок 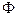 , либо непосредственно на множестве альтернатив
, либо непосредственно на множестве альтернатив  . В первом случае вводимое соотношение (свертка) интегрирует сочетание оценок
. В первом случае вводимое соотношение (свертка) интегрирует сочетание оценок  альтернативы
альтернативы 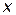 в скалярную характеристику качества. Данные априорные методы иногда называют методами построения сверток показателей (либо методами скаляризации). При этом различают эвристические и аксиоматические свертки.
в скалярную характеристику качества. Данные априорные методы иногда называют методами построения сверток показателей (либо методами скаляризации). При этом различают эвристические и аксиоматические свертки.
Среди эвристических сверток показателей выделяют псевдоуниверсальные (аддитивные, мультипликативные, функции минимума, расстояния в соответствии с заданной метрикой и т.п.) и специализированные (экономические, физические, вероятностные, функциональные или их комбинации).
При аксиоматическом подходе в качестве исходной информации при постановке задачи многокритериального выбора используется ряд аксиом (правил), которым должно удовлетворять результирующее отношение предпочтения. В зависимости от формы и способов задания аксиом различают теоретико-полезностные свертки, которые, как правило, представляются либо детерминированными функциями полезности, либо функциями ожидаемой полезности.
Вторая группа априорных методов решения многокритериальных задач основана на покомпонентном построении результирующих отношений предпочтения.
При этом различают паретовские, лексикографические, мажоритарные результирующие отношения предпочтения, первые два из которых в свою очередь подразделяются на классические, интервальные и пороговые, а последнее — на безынтервальное и интервальное результирующие отношения предпочтения.
Следует подчеркнуть, что выдвигаемое в априорных методах многокритериальной оптимизации требование получения дополнительной информации в виде принципа оптимальности базируется на предположении о том, что вся информация, по которой можно сформировать представление о лучшей альтернативе (и ЛПР способно это сделать), содержится в формальной модели задачи, т.е. в описании  и отображений
и отображений 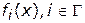 .
.
При разработке апостериорных методов многокритериальной оптимизации предполагается, что формальная модель задачи оптимизации не содержит достаточной информации, по которой ЛПР может сформулировать соответствующий целевой установке принцип оптимальности в таком виде, как того требуют априорные модели. В указанной ситуации ставится задача полного восстановления принципа оптимальности в явном виде по частичной дополнительной информации о нем. В качестве дополнительной информации используются предположения о свойствах принципа оптимальности, соответствующие физической сущности конкретной задачи принятия решения, и выявляемая определенными процедурами частичная информация, характеризующая предпочтения ЛПР на  и
и 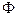 .
.
Восстанавливаемый принцип оптимальности задает формальную модель описания системы предпочтений ЛПР, которая в дальнейшем используется в качестве обобщенной целевой функции при решении задачи оптимизации. Указанная процедура имеет многоэтапный характер.
К многоэтапным методам могут быть отнесены адаптивные методы многокритериальной оптимизации, в которых не предполагается введение или полное восстановление принципа оптимальности в явном виде. В данных методах правдоподобные предположения о свойствах принципа оптимальности, свойствах системы предпочтений ЛПР и частичная информация о предпочтениях ЛПР используются непосредственно в процедурах поиска лучшей альтернативы. Другими словами, адаптивные методы позволяют ЛПР искать недоминируемые альтернативы при неявно заданном принципе оптимальности (результирующем отношении предпочтения).
Возможны различные сочетания (комбинации) перечисленных методов многокритериальной оптимизации: априорно-апостериорные методы, апостериорно-адаптивные методы и т.п. На рисунке 4.15 представлена классификация методов многокритериального выбора.
Теоретическая и практическая ценность различных методов многокритериального выбора определяется:
— обоснованностью принципов их построения и широтой класса задач принятия решений, в которых эти принципы реализуемы;
— возможностью выявления у ЛПР требуемой дополнительной информации;
— свойствами альтернатив и критериальных функций, степенью их соответствия целевой установке задачи.
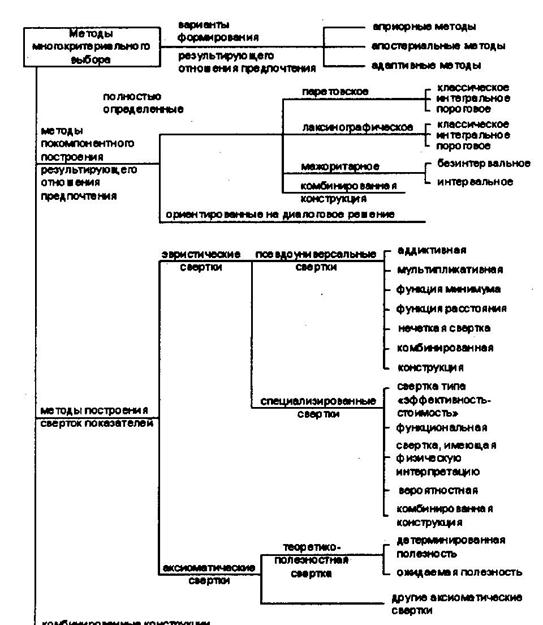
Рис. 4.15.
При этом каждый класс методов многокритериальной оптимизации имеет свои достоинства и недостатки. Из-за ограниченности объема учебника остановимся в дальнейшем более подробно на априорных методах многокритериального выбора. С апостериорными и адаптивными методами многокритериальной оптимизации можно более детально познакомиться, изучив литературу.
Методы покомпонентного построения результирующих отношений предпочтения
Основное содержание данных методов сводится к формированию сужающейся последовательности множеств (ядер): посредством введения на них… Необходимо отметить, что применение паретовских результирующих отношений… Из анализа определения классического лексикографического отношения предпочтения (см. формулу (4.30)) следует, что если…Методы построения результирующих отношений предпочтения на основе свертки показателей
Сущность данных методов многокритериальной оптимизации состоит в построении такого результирующего отношения предпочтения (в частности,… При применении прямых методов часто осуществляется модификация функций как в… С учетом введенных обозначений основные виды модификаций могут быть представлены следующим образом:РАЗДЕЛ 5. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОГО ВОЗДЕЙСТВИЯ СРЕДЫ
Характеристика задач принятия решений в условиях неопределенности среды
В зависимости от степени имеющихся знаний о среде используется та или иная форма ее описания, при этом различают следующие варианты: - д е т е р м и н и р о в а н н а я среда, действие которой на систему… - с т о х а с т и ч е с к а я среда, действие которой подчиняется известным (или неизвестным) вероятностным законам; …Принятие решений в условиях стохастической среды
(D(w), f(w)), wÎW, где D(w) - множество допустимых альтернатив, f(w) - целевая функция. На W вводится вероятностная структура (W,S,P) по Колмогорову А.Н.:Методы детерминизации.
f(x,w) ® max, gi(x,w) £ 0, i = 1,...,n. Далее будем иметь в виду обозначение go(x,w) = f(x,w).Методы имитационной оптимизации.
Преодоление указанных трудностей достигается на основе применения методов и м и т а ц и о н н о г о у с р е д н е н и я и методов с т о х а с т и ч… При имитационном усреднении произвольно (случайно) выбирается некоторое… Метод стохастической аппроксимации, как и метод имитационного усреднения, представляет собой итерационную процедуру…Принятие решений в условиях целенаправленной среды
К о н ф л и к т н о й с и т у а ц и е й назовем ситуацию, в которой сталкиваются интересы нескольких оперирующих сторон, преследующих различные… Конфликтная ситуация характеризуется: составом оперирующих сторон; целями,… Формализованную модель некоторой конфликтной ситуации называют и г р о й .Постановка задач игрового выбора.
(D ´ W, {fj, jÎG} ), где в качестве среды W выступают противники, преследующие свои цели fj, j… Т.к. имеется n оперирующих сторон, то множество альтернатив D ´ W представляется в виде декартова произведения…Матричные игры. Чистые и смешанные стратегии.
М а т р и ч н о й и г р о й называется конечная игра двух лиц с нулевой суммой. Тогда такая игра характеризуется конструкцией (D1 ´ D2, { f1, f2 }). (5.7)Методы нахождения оптимальных смешанных стратегий.
В качестве п о д г о т о в и т е л ь н о г о этапа при решении игры рассматривается этап упрощения игры, который заключается в: - преобразовании платежной матрицы к более простому виду; - выделении доминируемых стратегий игроков.Принятие решений в условиях неизвестной среды
П е р в о е направление связано с наблюдением за изменением состояний среды, и затем на основе собранной информации (статистики) строится… При анализе возможностей принятия решения в рамках данного направления следует… 1) для сбора и обработки статистики необходим ресурс времени, который на практике довольно часто отсутствует;– Конец работы –
Используемые теги: раздел, место, Роль, процессов, готовки, нятия, решений, общей, технологии, управления, сложными, организационно-техническими, системами, сотс0.16
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: РАЗДЕЛ 1.МЕСТО И РОЛЬ ПРОЦЕССОВ ПОДГОТОВКИ И ПРИНЯТИЯ РЕШЕНИЙ В ОБЩЕЙ ТЕХНОЛОГИИ УПРАВЛЕНИЯ СЛОЖНЫМИ ОРГАНИЗАЦИОННО-ТЕХНИЧЕСКИМИ СИСТЕМАМИ (СОТС
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов