Лекция 23. Метод главных компонентов в задаче сжатия
Идея сжатия сигнала на основе разложения по ортогональному базису была изложена выше. Рассмотренные базисы являются универсальными и не учитывают особенность сигнала. Когда имеется набор сигналов одной природы, возникает вопрос о выборе оптимального базиса, пригодного для сжатия всего семейства. Эта задача решается с помощью метода главных компонентов. Сначала нам понадобится вспомогательное утверждение из линейной алгебры.
Предложение 1. Пусть имеется вещественная симметрическая матрица 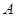 и натуральное
и натуральное 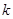 , меньше чем размер матрицы. Среди матриц
, меньше чем размер матрицы. Среди матриц 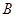 вида
вида 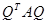 , где
, где 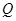 - ортогональная матрица, выбирается такая, в которой сумма первых
- ортогональная матрица, выбирается такая, в которой сумма первых 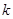 диагональный элементов максимальна. Тогда эта сумма совпадает с суммой
диагональный элементов максимальна. Тогда эта сумма совпадает с суммой 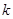 наибольших корней
наибольших корней 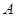 .
.
Доказательство. Очевидно, что максимум достигается на некоторой матрице 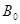 . Положим
. Положим 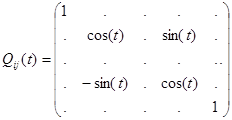 - элементарный поворот, затрагивающий строки и столбцы с номерами
- элементарный поворот, затрагивающий строки и столбцы с номерами 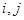 . Обозначим через
. Обозначим через 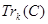 сумму первых
сумму первых 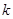 диагональных элементов матрицы
диагональных элементов матрицы 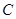 . По определению
. По определению 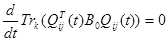 при
при  . Очевидно, что
. Очевидно, что 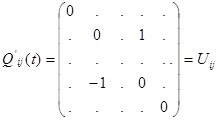 при
при  . В этих обозначениях производная в нуле принимает вид
. В этих обозначениях производная в нуле принимает вид 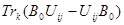 . Взяв индексы
. Взяв индексы 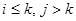 , получим, что
, получим, что 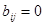 . Это означает, что искомая матрица
. Это означает, что искомая матрица 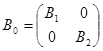 . Поскольку набор корней матриц
. Поскольку набор корней матриц 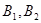 исчерпывает множество корней
исчерпывает множество корней 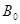 , отсюда следует утверждение.
, отсюда следует утверждение.