Р е ш е н и е.
Необходимо выбрать две точки (два момента времени) так, чтобы число ошибок, найденных на интервале А ÷ В, было больше, чем на интервале от О ÷ А. Затем выполнить следующие расчеты:
- ошибка, найденная соответственно на этапе тестирования О ÷ А
ε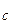 ( τ
( τ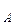 ) =
) = 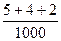 =
= 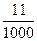 = 0,011;
= 0,011;
- то же на этапе А ÷ В
ε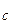 ( τ
( τ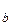 ) =
) = 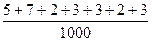 =
= 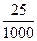 = 0,025;
= 0,025;
- время от начала тестирования до А
τ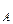 = 4 + 4 + 3 = 11;
= 4 + 4 + 3 = 11;
- время на интервале А ÷ В
τ = 4 + 6 + 4 + 4 + 5 + 3 + 2 = 28;
= 4 + 6 + 4 + 4 + 5 + 3 + 2 = 28;
- интенсивность появления ошибок на 1-м интервале
λ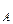 =
= 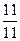 = 1;
= 1;
- интенсивность появления ошибок на 2-м интервале
λ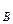 =
= 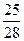 = 0,89;
= 0,89;
- первоначальное количество ошибок в ПС
Е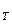 =
= 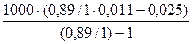 =
= 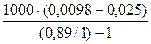 =
= 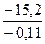 =
=
= 138 ошибок;
- константа С будет иметь значение
С = 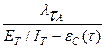 =
= 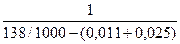 =
= 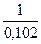 = 9,8.
= 9,8.
Подставляя различные t (время) при τ = 11+28 = 39. можно рассчитать по формуле (2) вероятность безотказной работы в течение соответствующего времени.
б) Позднее автором предложена модифицированная модель, не учитывающая число машинных команд, т.е. независимая от I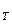 .
.
Функция частоты отказов в течение i-го интервала тестирования остается постоянной и равна:
Z(t) = (Е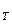 – n
– n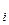 )∙С, t ≥ 0, i = 1, 2, . . . , m.
)∙С, t ≥ 0, i = 1, 2, . . . , m.
Известные параметры модели Е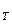 и С автор предлагает вычислять из следующих соотношений:
и С автор предлагает вычислять из следующих соотношений:
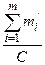 –
– 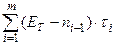 = 0;
= 0;
С∙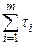 –
– 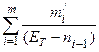 = 0,
= 0,
где τ – время i-го прогона (время i-го интервала);
– время i-го прогона (время i-го интервала);
m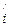 – число прогонов, завершившихся отказом в i-м интервале (число ошибок в i-м интервале);
– число прогонов, завершившихся отказом в i-м интервале (число ошибок в i-м интервале);
m – общее число тестовых интервалов;
n – общее число ошибок, обнаруженных (но не включенных) к i-му интервалу.
– общее число ошибок, обнаруженных (но не включенных) к i-му интервалу.
Все эти данные можно получить в ходе тестирования. Вычислив значения параметров Е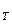 и С, можно определить следующие показатели:
и С, можно определить следующие показатели:
1) число оставшихся ошибок в ПС
N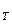 = Е
= Е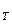 – n;
– n; 
2) надежность
R(t) = exp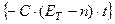 , t ≥ 0.
, t ≥ 0.
Достоинство этой модели по сравнению с предыдущей заключается в следующем. Теперь можно исправлять ошибки, внося изменения в текст программы в ходе тестирования, не разбивая процесс на этапы, чтобы удовлетворить требованию постоянства числа машинных инструкций.
2) Модель La Padula.По этой модели выполнение последовательноститестов производится в m этапов. Каждый этап заканчивается внесением изменений (исправлений) в ПС. Возрастающая функция надежности базируется на числе ошибок, обнаруженных в ходе каждого тестового прогона.
Надежность ПС в течение i-го этапа:
R(t) = R(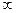 ) –
) – 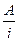 , i = 1, 2, …,
, i = 1, 2, …,
где А – параметр роста;
R(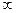 ) = limR(i) – предельная надежность ПС.
) = limR(i) – предельная надежность ПС.
i → 
Эти неизвестные величины автор предлагает вычислить, решив следующие уравнения:

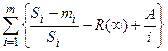 = 0;
= 0;

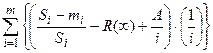 = 0,
= 0,
где S – число тестов;
– число тестов;
m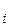 – число отказов во время i-го этапа;
– число отказов во время i-го этапа;
m – число этапов;
i = 1, 2, . . . , m.
Определяемый по этой модели показатель есть надежность ПС на i-м этапе.
R(i) = R(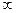 ) –
) – 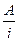 , i = m + 1, m + 2, …
, i = m + 1, m + 2, …
Преимущество модели заключается в том, что она является прогнозной. Основываясь на данных, полученных в ходе тестирования, она дает возможность предсказать вероятность безотказной работы программы на последующих этапах ее выполнения.
3) Модель Джелинского-Моранды. Эта модель относится к динамическим моделям непрерывного времени. Исходные данные для использования этой модели собираются в процессе тестирования ПС. При этом фиксируется время до очередного отказа. Основное положение, на котором базируется модель, заключается в следующем. Значение интервалов времени тестирования между обнаружением 2-х ошибок имеет экспоненциальное распределение с частотой ошибок (или интенсивностью отказов), пропорциональной числу еще не выявленных ошибок. Каждая обнаруженная ошибка устраняется. Число оставшихся ошибок уменьшается на единицу.
Функция плотности распределения времени обнаружения i-й ошибки, отсчитываемого от момента выявления (i – 1)-й ошибки, имеет вид:
R(t ) = λ
) = λ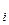 ∙e
∙e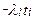 , (10)
, (10)
где λ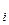 – частота отказов (интенсивность отказов), которая пропорциональна числу еще не выявленных ошибок в программе.
– частота отказов (интенсивность отказов), которая пропорциональна числу еще не выявленных ошибок в программе.
λ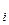 = C∙(N – i + 1), (11)
= C∙(N – i + 1), (11)
где N – число ошибок, первоначально присутствующих в программе;
С – коэффициент пропорциональности.
Наиболее вероятные значения величин  и
и 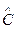 (оценка максимального правдоподобия) можно определить на основе данных, полученных при тестировании. Для этого фиксируют время выполнения программы до очередного отказа t
(оценка максимального правдоподобия) можно определить на основе данных, полученных при тестировании. Для этого фиксируют время выполнения программы до очередного отказа t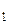 , t
, t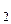 , t
, t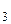 ,…, t
,…, t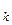 .
.
Значения  и
и 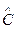 предлагается получить, решив систему уравнений:
предлагается получить, решив систему уравнений:
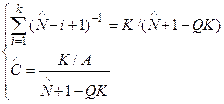
 , (12)
, (12)
где Q = B/A∙K; A = 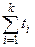 ; B =
; B = 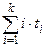 .
.
Поскольку полученные значения  и
и 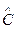 – вероятностные и точность их зависит от количества интервалов тестирования (или количества ошибок), найденных к моменту оценки надежности, то асимптотические оценки дисперсий авторы предлагают определить с помощью следующих формул:
– вероятностные и точность их зависит от количества интервалов тестирования (или количества ошибок), найденных к моменту оценки надежности, то асимптотические оценки дисперсий авторы предлагают определить с помощью следующих формул:
Var( ) = K/C
) = K/C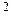 ∙D;
∙D;
Var(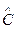 ) = S/D,
) = S/D,
где D = K∙S/C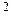 – A
– A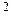 и S =
и S = 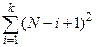 .
.
Чтобы получить числовые значения λ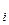 , нужно подставить вместо N и С их возможные значения
, нужно подставить вместо N и С их возможные значения  и
и 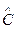 . Рассчитав К значений по формуле (11) и подставив их в формулу (10), можно определить вероятность безотказной работы на различных временных интервалах. На основе полученных расчетных данных строится график зависимости вероятности безотказной работы от времени.
. Рассчитав К значений по формуле (11) и подставив их в формулу (10), можно определить вероятность безотказной работы на различных временных интервалах. На основе полученных расчетных данных строится график зависимости вероятности безотказной работы от времени.
4) Модель Шика-Волвертона. Модификация модели Джелинского-Моранды для случая возникновения на рассматриваемом интервале более одной ошибки предложена Волвертоном и Шиком. При этом считается, что исправление ошибок производится после истечения интервала времени, на котором они возникли. В основе модели Шика-Волвертона лежит предположение, согласно которому частота ошибок пропорциональна не только количеству ошибок в программах, но и времени тестирования. Т.е., вероятность обнаружения ошибок с течением времени возрастает. Частота ошибок (интенсивность обнаружения ошибок) λ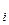 предполагается постоянной в течение интервала времени t
предполагается постоянной в течение интервала времени t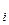 и пропорциональна числу ошибок, оставшихся в программе по истечении (i – 1)-го интервала. Но она пропорциональна также и суммарному времени, уже затраченному на тестирование, включая среднее время выполнения программы в текущем интервале:
и пропорциональна числу ошибок, оставшихся в программе по истечении (i – 1)-го интервала. Но она пропорциональна также и суммарному времени, уже затраченному на тестирование, включая среднее время выполнения программы в текущем интервале:
λ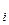 = C∙(N – n
= C∙(N – n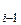 )∙(T
)∙(T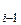 +
+ 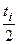 ).
).
В данной модели наблюдаемым событием является число ошибок, обнаруживаемых в заданном временном интервале, а не время ожидания каждой ошибки, как это было для модели Джелинского-Моранды. В связи с этим модель относя к группе дискретных динамических моделей, а уравнения для определения 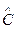 и
и  имеют несколько иной вид:
имеют несколько иной вид:
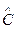 =
= 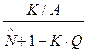 ;
; 
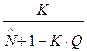 =
= 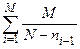 , (13)
, (13)
где А = 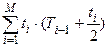 ;
;
В = 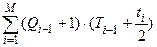 ; смысл В – тот же, что и в мод. Дж.-Моранды;
; смысл В – тот же, что и в мод. Дж.-Моранды;
t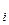 – продолжительность временного интервала, в котором наблюдается М
– продолжительность временного интервала, в котором наблюдается М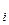 ошибок;
ошибок;
Т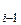 – время, накопленное за (i – 1) интервалов;
– время, накопленное за (i – 1) интервалов;
Т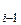 =
= 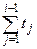 , Т
, Т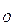 = 0;
= 0;
n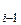 =
= 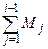 , n
, n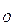 = 0;
= 0;
К = 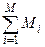 = n
= n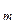 – суммарное число обнаруженных ошибок.
– суммарное число обнаруженных ошибок.
При М =1 уравнения (13) приобретают вид уравнений (12), М = К, n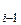 = i – 1.
= i – 1.
Т.о., модель Джелинского-Моранды является частным случаем модели Шика-Волвертона для случая, когда при тестировании фиксируется время до появления очередной ошибки.
5) Модель Муса. Модель Муса относят к динамическим моделям непрерывного времени. Это значит, что в процессе тестирования фиксируется время выполнения программы (тестового прогона) до очередного отказа. Но считается, что не всякая ошибка ПС может вызвать отказ. Поэтому допускается обнаружение более одной ошибки при полнении программы до возникновения очередного отказа.
Считается, что на протяжении всего ЖЦ ПС может произойти М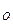 отказов и при этом будут выявлены все N
отказов и при этом будут выявлены все N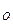 ошибки, которые присутствовали в ПС до начала тестирования. Общее число отказов М
ошибки, которые присутствовали в ПС до начала тестирования. Общее число отказов М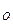 связано с первоначальным числом ошибок N
связано с первоначальным числом ошибок N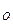 соотношением
соотношением
N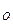 = В· М
= В· М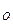 , (14)
, (14)
где В – коэффициент уменьшения числа ошибок.
В момент, когда производится оценка надежности, после проведения тестирования, на которое потрачено определенное время τ, зафиксировано m отказов и n выявлено ошибок.
Тогда из соотношения
n = В·m (15)
можно определить коэффициент уменьшения числа ошибок В как число, характеризующее количество устраненных ошибок, приходящихся на один отказ.
В модели Мусса различают два вида времени:
1) суммарное время функционирования τ, которое учитывает чистое время тестирования до контрольного момента, когда производится оценка надежности;
2) оперативное время t – время выполнения программы, планируемое от контрольного момента и далее, при условии, что дальнейшего устранения ошибок не будет (время безотказной работы в процессе эксплуатации).
Для суммарного времени функционирования τ предполагается:
• интенсивность отказов пропорциональна числу неустраненных ошибок;
• скорость изменения числа устраненных ошибок, измеряемая относительно суммарного времени функционирования, пропорциональна интенсивности отказов.
Один из основных показателей надежности, который рассчитывается по модели Муса, – средняя наработка на отказ. Этот показатель определяется как математическое ожидание временного интервала между последовательными отказами и связан с надежностью
Т = 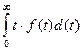 =
= 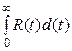 ,
,
где t – время работы до отказа.
Если интенсивность отказов постоянна (т.е. когда длительность интервалов между последовательными отказами имеет экспоненциальное распределение), то средняя наработка на отказ обратно пропорциональна интенсивности отказов. По модели Муса средняя наработка на отказ зависит от суммарного времени функционирования τ:
Т = Т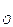 ∙exp
∙exp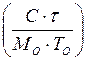 , (16)
, (16)
где Т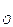 – средняя наработка на отказ в начале испытаний (тестирования);
– средняя наработка на отказ в начале испытаний (тестирования);
С – коэффициент сжатия тестов, который вводится для устранения избыточности при тестировании. Если, например, один час тестирования соответствует 12 ч работы в реальных условиях, то коэффициент сжатия тестов равен 12.
Параметр Т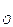 – средняя наработка на отказ до начала тестирования, можно предсказать из следующего соотношения:
– средняя наработка на отказ до начала тестирования, можно предсказать из следующего соотношения:
Т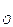 =
= 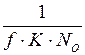 , (17)
, (17)
где f – средняя скорость исполнения программы, отнесенная к числу команд (операторов);
К – коэффициент проявления ошибок, связывающий частоту возникновения ошибок со “скоростью ошибок”. Она представляет собой скорость, с которой бы встречались ошибки программы, если бы программа выполнялась линейно (последовательно по командам). В настоящее время значение К приходится определять эмпирическим путем по однотипным программам. Его значение изменяется от 1,54∙10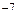 до 3,99∙10
до 3,99∙10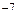 ;
;
N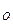 – начальное число ошибок. N
– начальное число ошибок. N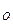 можно рассчитать с помощью другой модели, позволяющей определить эту величину на основе статистических данных, полученных при тестировании (например, модель Шумана). Надежность R для оперативного периода
можно рассчитать с помощью другой модели, позволяющей определить эту величину на основе статистических данных, полученных при тестировании (например, модель Шумана). Надежность R для оперативного периода 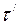 выражается равенством
выражается равенством
R = exp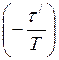 . (18)
. (18)
Если в договоре с заказчиком оговорена требуемая величина наработки на отказ Т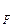 , то можно определить число отказов
, то можно определить число отказов 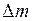 и дополнительное время функционирования (тестирования)
и дополнительное время функционирования (тестирования) 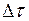 , обеспечивающее заданное Т
, обеспечивающее заданное Т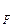 . Их можно рассчитать по формулам:
. Их можно рассчитать по формулам:
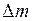 = М
= М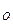 ∙ Т
∙ Т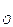 ∙
∙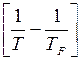 ; (19)
; (19)
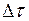 =
= 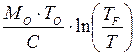 . (20)
. (20)
По результатам тестовых испытаний можно определить значение коэффициента В из соотношения (15) и М – из соотношения (14). По договорной величине требуемой средней наработки на отказ Т
– из соотношения (14). По договорной величине требуемой средней наработки на отказ Т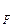 и рассчитанной по модели Мусса текущей средней наработки на отказ Т можно сделать заключение о необходимости продолжать или, возможно, закончить тестирование программ. В случае необходимости продолжения работ по тестированию для достижения требуемой средней наработки на отказ модель дает возможность предсказать число возможных отказов
и рассчитанной по модели Мусса текущей средней наработки на отказ Т можно сделать заключение о необходимости продолжать или, возможно, закончить тестирование программ. В случае необходимости продолжения работ по тестированию для достижения требуемой средней наработки на отказ модель дает возможность предсказать число возможных отказов 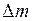 – формула (19) – и дополнительное время тестирования
– формула (19) – и дополнительное время тестирования 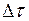 – формула (20).
– формула (20).
6) Модель переходных вероятностей. Эта модель основана на Марковском процессе, протекающем в дискретной системе с непрерывным временем. Процесс, протекающий в системе, называется Марковским или процессом без последствий, если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящее время (t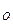 ) и не зависит от того, каким образом система пришла в это состояние. Процесс тестирования ПС рассматривается как Марковский процесс.
) и не зависит от того, каким образом система пришла в это состояние. Процесс тестирования ПС рассматривается как Марковский процесс.
В начальный момент времени тестирования (t = 0) в ПС было n ошибок. Предполагается, что в процессе тестирования выявляется по одной ошибке. Тогда последовательность состояний системы 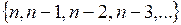 и т.д. соответствует периодам времени, когда предыдущая ошибкам уже исправлена, а новая еще не обнаружена. Например, в состоянии n–5 пятая ошибка уже исправлена, а шестая еще не обнаружена.
и т.д. соответствует периодам времени, когда предыдущая ошибкам уже исправлена, а новая еще не обнаружена. Например, в состоянии n–5 пятая ошибка уже исправлена, а шестая еще не обнаружена.
Последовательность состояний 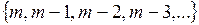 и т.д. соответствует периодам времени, когда ошибки исправляются. Например, в состоянии m–1 вторая ошибка уже обнаружена, но еще не исправлена. Ошибки обнаруживаются с интенсивностью
и т.д. соответствует периодам времени, когда ошибки исправляются. Например, в состоянии m–1 вторая ошибка уже обнаружена, но еще не исправлена. Ошибки обнаруживаются с интенсивностью 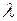 , а исправляются с интенсивностью
, а исправляются с интенсивностью 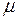 .
.
Предположим, в какой-то момент времени процесс тестирования остановился. Совокупность возможных состояний системы будет:
S = 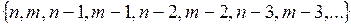 .
.
Система будет переходить из одного состояния в другое с определенной вероятностью Р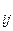 . Время перехода системы из одного состояния в другое бесконечно мало.
. Время перехода системы из одного состояния в другое бесконечно мало.
Вероятность перехода из состояния n–k в состояние m–k есть 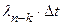 для k = 0, 1, 2, . . .. Соответственно вероятность перехода из состояния m–k в состояние n–k +1 будет
для k = 0, 1, 2, . . .. Соответственно вероятность перехода из состояния m–k в состояние n–k +1 будет 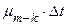 для k = 0, 1, 2, . . ..
для k = 0, 1, 2, . . ..
Общая схема модели представлена на Рис. 2.
1-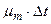 1-
1-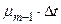 1-
1- 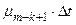 1-
1-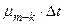
 | |||||||
 |  | ||||||
 | |||||||

 m m-1 m-k+1 m-k
m m-1 m-k+1 m-k
 |  | ||||||||
 | |||||||||
 |  | ||||||||
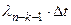
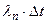
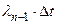
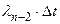
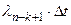
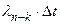
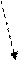 |
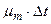
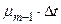
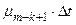
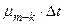



 n n-1 n-2 n-k+1 n-k n-k-1
n n-1 n-2 n-k+1 n-k n-k-1
1-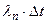 1-
1-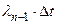 1-
1-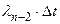 1-
1-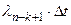 1-
1-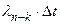 1-
1-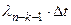
Рис. 2. Модель многих состояний ПС
Если считать, что 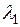 и
и 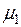 зависят от текущего состояния системы, то можно составить следующую матрицу переходных вероятностей:
зависят от текущего состояния системы, то можно составить следующую матрицу переходных вероятностей:
 1-
1-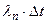
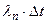 0 0… 0……
0 0… 0……
0 1-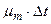
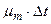 0….. 0…...
0….. 0…...
0 0 1-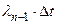
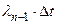 0……
0……
0 0 0 1-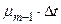
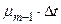
……………………………………………………………………
………………………………………………..........1-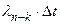
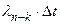
...…………………………………………………...0 1-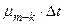
Пусть S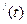 – случайная переменная, которой обозначено состояние системы в момент времени t. В любой момент времени система может находиться в 2-х возможных состояниях: работоспособном либо неработоспособном (момент исправления очередной ошибки).
– случайная переменная, которой обозначено состояние системы в момент времени t. В любой момент времени система может находиться в 2-х возможных состояниях: работоспособном либо неработоспособном (момент исправления очередной ошибки).
Вероятности нахождения системы в том или ином состоянии определяются как:
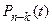 = Р(S
= Р(S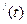 = n – k), k = 0, 1, 2, . . .
= n – k), k = 0, 1, 2, . . .
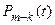 = Р(S
= Р(S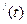 = m – k), k = 0, 1, 2, . . .
= m – k), k = 0, 1, 2, . . .
Готовность системы определяется как сумма вероятностей нахождения ее в работоспособном состоянии:
А(t) = 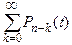 .
.
Под готовностью системы к моменту времени t понимается вероятность того, что система находится в рабочем состоянии во время t. После t времени отладки, за которое уже выявлено К ошибок, система находится в состоянии n – k, т.е. К-я ошибка исправлена, а (К+1)-я еще не обнаружена. Для такого положения надежность системы может быть определена из состояния:
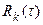 = е –
= е – 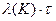 ,
,
где 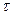 – интервал времени, когда может появиться (К+1)-я ошибка;
– интервал времени, когда может появиться (К+1)-я ошибка;
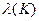 – принятая постоянная интенсивность проявления ошибок.
– принятая постоянная интенсивность проявления ошибок.
Рассмотрим решение модели для случая, когда интенсивность появления ошибок 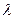 и интенсивность их исправления
и интенсивность их исправления 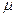 – постоянные величины. Составляется следующая система дифференциальных уравнений:
– постоянные величины. Составляется следующая система дифференциальных уравнений: 
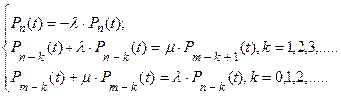
Начальными условиями для решения системы могут являться:
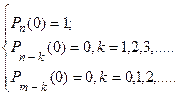
При имеющихся начальных условиях система уравнений может быть решена классически или с использованием преобразований Лапласа. В результате решения определяются Р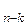 и Р
и Р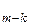 для случая, когда
для случая, когда 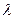 и
и 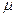 – константы. Для общего случая отбросим ограничение постоянства интенсивностей появления и исправления ошибок и предположим, что
– константы. Для общего случая отбросим ограничение постоянства интенсивностей появления и исправления ошибок и предположим, что
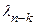 =
= 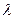 (К);
(К);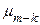 =
= 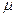 (К), k = 0, 1, 2, . . . ,
(К), k = 0, 1, 2, . . . ,
т.е. являются функциями числа ошибок, найденных к этому времени в ПС. Система дифференциальных уравнений для такого случая имеет вид:
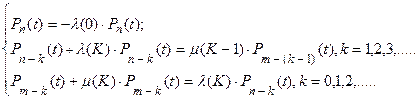
Начальные условия для решения системы будут:
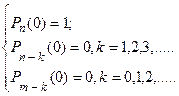
Система может быть решена методом итераций Эйлера. Предполагается, что в начальный период использования модели значения 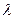 и
и 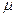 должны быть получены на основе предыдущего опыта разработчика. В свою очередь, модель позволяет накапливать данные об ошибках. Это дает возможность повышения точности анализа на основе предыдущего моделирования. Практическое использование модели требует громоздких вычислений и делает необходимым наличие ее программной поддержки.
должны быть получены на основе предыдущего опыта разработчика. В свою очередь, модель позволяет накапливать данные об ошибках. Это дает возможность повышения точности анализа на основе предыдущего моделирования. Практическое использование модели требует громоздких вычислений и делает необходимым наличие ее программной поддержки.