рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Информатика
- /
- Кафедра математики и информатики. Практикум
Реферат Курсовая Конспект
Кафедра математики и информатики. Практикум
Кафедра математики и информатики. Практикум - раздел Информатика, Государственное Образовательное Учреждение Высшего П...
Государственное образовательное учреждение
высшего профессионального образования
«Рязанский государственный медицинский университет
имени академика И.П.Павлова
Федерального агентства по здравоохранению
и социальному развитию»
Кафедра математики и информатики

Практикум
Рязань 2009
УДК 517.2/.3 + 519.2 (075.8)
ББК 22.161.1+22.17
М 34
Авторы – составители: М.П. Булаев, М.Н. Дмитриева, Н.В. Дорошина, И.С. Маркова, О.А. Назарова, Е.В. Прохорова
Рецензенты: С.П. Вихров, д.ф.-м.н., профессор Рязанского
государственного радиотехнического
университета;
А.Н. Пылькин, д.т.н., профессор Рязанского государственного радиотехнического университета;
|
Предназначен для первоначального изучения дифференциального и интегрального исчисления, теории вероятностей и математической статистики. Практикум рассчитан на студентов специальностей 060101, 060104, 060105, 060108, 030302 дневной, вечерней и заочной форм образования.
Он также может быть полезен студентам других гуманитарных специальностей.
УДК 517.2/.3+519.2 (075.8)
ББК 22.161.1+22.17
Табл.: 60 Ил.: 38 Библиогр.: 10 назв.
Печатается по решению Учебно-методического Совета Рязанского государственного медицинского университета.
 ã ГОУ ВПО «РязГМУросздрава», 2009
ã ГОУ ВПО «РязГМУросздрава», 2009
Глава 1. Предел функции
Определение предела
Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в… Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число D>0, что для всех х…Операции над пределами
1. Предел постоянной есть сама постоянная: 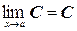 , где С = const.
, где С = const.
Следующие свойства справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а;
2. Предел суммы (разности) равен сумме (разности) пределов:
 ;
;
3. Предел произведения равен произведению пределов:
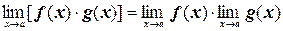 ;
;
4. Постоянную можно выносить за знак предела:
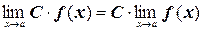 ;
;
5. Предел отношения равен отношению пределов:
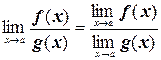 , при
, при  ;
;
6. Если f(x)>0 вблизи точки х = а и  , то А>0.
, то А>0.
Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0;
7. Если g(x) £ f(x) £ u(x) вблизи точки х = а и  , то и
, то и  ;
;
8. 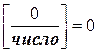 ;
;
9. 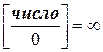 ;
;
10. 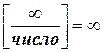 ;
;
11.  ;
;
12. Неопределенность вида  можно раскрыть, если числитель и знаменатель дроби разделить на высшую степень переменной;
можно раскрыть, если числитель и знаменатель дроби разделить на высшую степень переменной;
13. Неопределенность вида 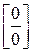 можно раскрыть, если числитель и знаменатель дроби разложить на множители и сократить.
можно раскрыть, если числитель и знаменатель дроби разложить на множители и сократить.
Замечательные пределы
Найдем предел отношения двух многочленов, т.е. , где P(x) = a0xn + a1xn–1 +…+an, Q(x) = b0xm + b1xm–1 +…+bm. Преобразуем данную…Примеры
№1. Используя свойства пределов функций, найти следующие пределы:
а) 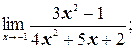
б) 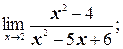
в) 
г) 
Решение.
а) Применяя теорему о действиях над пределами функций, получим:
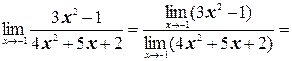
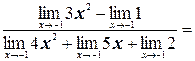
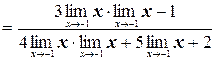
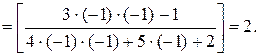
б) Так как пределы числителя и знаменателя при х®2 равны нулю, то мы имеем неопределенность вида  . «Раскроем» эту неопределенность (т.е. избавимся от нее), разложив числитель и знаменатель на множители и сократив их далее на общий множитель х– 2:
. «Раскроем» эту неопределенность (т.е. избавимся от нее), разложив числитель и знаменатель на множители и сократив их далее на общий множитель х– 2:
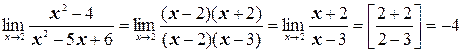 .
.
в) Здесь мы также имеем неопределенность вида  . Домножим числитель и знаменатель дроби на выражение, сопряженное к числителю (избавимся от иррациональности в числителе):
. Домножим числитель и знаменатель дроби на выражение, сопряженное к числителю (избавимся от иррациональности в числителе):

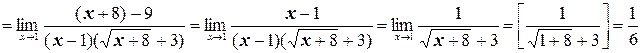
г) Числитель и знаменатель дроби – бесконечно большие функции, поэтому здесь имеет место неопределенность вида  . Раскроем эту неопределенность. Поделим числитель и знаменатель дроби на высшую степень х, т.е. на х2:
. Раскроем эту неопределенность. Поделим числитель и знаменатель дроби на высшую степень х, т.е. на х2:
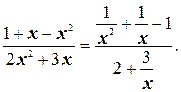
Таким образом,
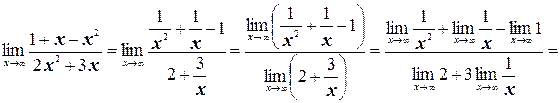

№2. Найти пределы:
а) 
б) 
в) 
г) 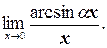
Решение.
а) Сделаем замену у=αх; тогда у®0 при х®0 и  . В последнем равенстве мы воспользовались первым замечательным пределом. Таким образом,
. В последнем равенстве мы воспользовались первым замечательным пределом. Таким образом, 
б) Поделим числитель и знаменатель дроби под знаком предела на х, после чего воспользуемся предыдущим пунктом:

в) Сводя предел к первому замечательному пределу, сделаем замену у=х–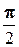 . Тогда у®0 при х®
. Тогда у®0 при х®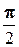 , а х=у+
, а х=у+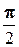 , откуда:
, откуда:
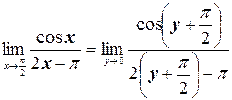
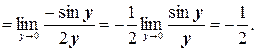
Во втором равенстве в этой цепочке мы использовали формулу приведения, а в последнем – первый замечательный предел.
г) Так как х®0, то воспользуемся эквивалентностью №4:
 .
.
Варианты заданий
№1.1. Найти пределы:
а)  ;
;
б)  ;
;
в)  ;
;
г) 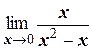 ;
;
д)  ;
;
е)  ;
;
ж) 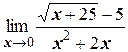 ;
;
з)  ;
;
и) 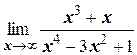 ;
;
к)  ;
;
л)  ;
;
м) 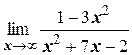 .
.
№1.2. Найти пределы:
а)  ;
;
б)  ;
;
в)  ;
;
г) 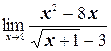 ;
;
д)  ;
;
е) 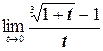 ;
;
ж) 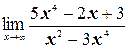 ;
;
з)  ;
;
и) 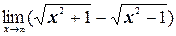 ;
;
к)  .
.
№1.3. Найти пределы:
а) 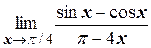 ;
;
б) 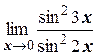 ;
;
в)  ;
;
г) 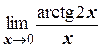 ;
;
д)  ;
;
е) 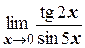 ;
;
ж) 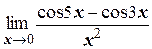 ;
;
з) 
Контрольные вопросы
Глава 2. Производная и дифференциал
Понятие производной
Рассмотрим функцию y=f(x). Предположим, что x0 внутренняя точка множества определения функции. Зададим приращение аргумента Dx¹0 такое, что… Если существует предел отношения приращения функции к приращению аргумента при… Обозначение: .Геометрический и физический смысл производной
Пусть функция y=f(x) имеет производную в точке x0. Тогда существует касательная к графику этой функции в точке М0(x0, у0), уравнение которой имеет… . При этом , где a – угол наклона этой касательной к положительному направлению оси ОХ (рис. 2.1).Таблица производных
1. С ¢ = 0, где С–постоянная
2. (xm)¢ = mxm–1
3. 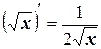
4. 
5. 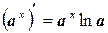
6. 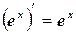
7. 
8. 
9. 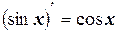
10. 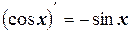
11. 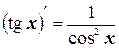
12. 
13. 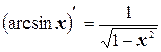
14. 
15. 
16. 
Основные правила дифференцирования
Пусть u и v – функции, дифференцируемые в точке х. Тогда 1. Производная суммы двух дифференцируемых функций равна сумме их… (u+v) ′=u′+v′Производные высших порядков
Производная f ′ (x) от функции f(x) называется также производной первого порядка. В свою очередь производная от функции f ′ (x) тоже… Вторая производная обозначается символами: f′′(х) (читается: «эф… Исходя из определения второй производной, можно записать: .Дифференциал функции
Если функция f(х) дифференцируема в точке х0, то ее приращение можно представить в виде Δf(х0) = f /(x0)×Δх + α(Δх)× Δх. (2.3) … В этом случае выражение f /(x0)×Δх, линейно зависящее от Δх, называется дифференциалом функции f(х) в…Геометрический смысл и свойства дифференциала
Из треугольника DMKL выразим сторону KL: KL = tga×Dx = f /(x)×Dx = dy Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в…Дифференциалы высших порядков
Пусть функция y=f(x) дифференцируема на интервале (a; b). Тогда в каждой точке этого интервала определен дифференциал dу=f / (x)dx функции f(x),… Дифференциалом второго порядка (или вторым дифференциалом) от функции y=f(x) в… Дифференциал второго порядка обозначается d2f(х) или d2y (читается: «дэ два игрек»). Таким образом, d2y=d(dy).…Примеры
№1. Найти производную функции  .
.
Решение.
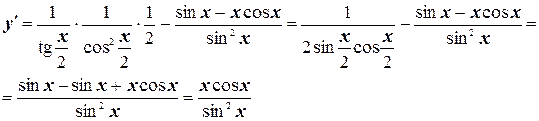
№2. Найти производную функции 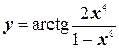 .
.
Решение.
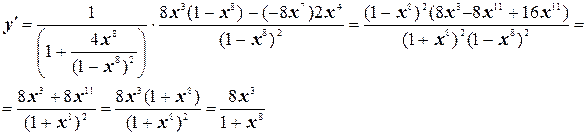
№3. Точка движется по закону х(t) = t – sin t. Определить скорость и ускорение точки в момент времени t=4с.
Решение.
Воспользуемся формулой (3.3.1):
V= х′(t) = (t – sin t) ′ = 1 – cos t,
V(4)=1–cos 4»1,6 (м/с).
Аналогично по формуле (3.3.2):
а= V′ = (1 – cos t) ′ = sin t,
а(4)=sin 4»–0,76 (м/с2).
№4. Найти дифференциал функции f (x) = ln(x2+1).
Решение.
По формуле (3.8.1) получим
df = (ln (x2+1)) ′dx = 
№5. Найти производную второго порядка от функции f (x) = sin2 х.
Решение.

№6. Вычислить значение дифференциала функции f (x) = х3+2х, когда х изменяется от 1 до 1,1.
Решение.
Прежде находим общее выражение для дифференциала этой функции:
df = (x3+2x) ′dx = (3x2+2)dx.
Определим приращение аргумента Δx=dx = 1,1–1=0,1.
Подставляя значения dx=0,1 и x=1 в последнюю формулу, получаем искомое значение дифференциала: df=0,5.
№7. Используя понятие дифференциала, найти приближенное значение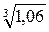 .
.
Решение.
Рассмотрим функцию f(x)=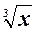 . Требуется вычислить значение f(1,06). Выберем х0 = 1, Δх = 0,06 и воспользуемся формулой (3.7.2)
. Требуется вычислить значение f(1,06). Выберем х0 = 1, Δх = 0,06 и воспользуемся формулой (3.7.2)
f(1+0,06) ≈ f (1)+f /(1) 0,06=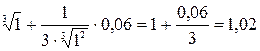 .
.
Здесь мы воспользовались равенством 
Варианты заданий
№2.1. Найти производные следующих функций:
1. у = сos3x;
2. 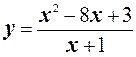 ;
;
3. у=(3x+2)(x2+4x–1);
4.  ;
;
5.  ;
;
6. 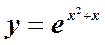 ;
;
7.  ;
;
8. 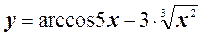 ;
;
9.  ;
;
10. 
11. 
12. 
13. 
14. у =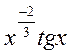
15. у = 
16. 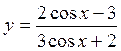
17. 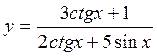
18. 
19. у = sin3(2x + π/6)
20. y = (3x+1)2(2x-3)7
21. 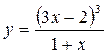
22. y = cos(sin(cos(sinx)))
23. y = x3 + ex –cos3x
24. 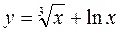
25. 
26. 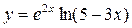
27. 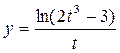
28. 
29. 
30. 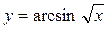
31. 
32. y = xtgx
33. y = xcosx
34. y = xsin2x
35. y = 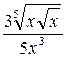
№2.2. Найти производную данной функции в точке х0:
1. 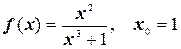 ;
;
2.  ;
;
3. 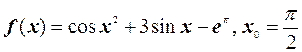 ;
;
4. 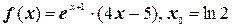 .
.
№2.3. Найти производные указанных порядков для следующих функций:
1. y = ln cos x, y//=?;
2. y = 5x, y///=?;
3. y = sin2 x, y///=?;
4.  ;
;
5.  , у//=?;
, у//=?;
6.  .
.
№2.4. Решить следующие задачи:
1. Составить уравнение касательной к гиперболе 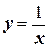 в точке с абсциссой х=–0,5.
в точке с абсциссой х=–0,5.
2. Точка движется по прямой так, что ее расстояние s от начального пункта через t сек. равно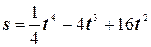 . В какие моменты точка была в начальном пункте? В какие моменты ее скорость равна нулю?
. В какие моменты точка была в начальном пункте? В какие моменты ее скорость равна нулю?
3. Количество вещества, протекшее через проводник, начиная с момента времени t=0, дается формулой Q=2t2+3t+1 (кулонов). Найти силу тока в конце пятой секунды.
4. Составить уравнения касательных к линии  в точках ее пересечения с осью абсцисс.
в точках ее пересечения с осью абсцисс.
№2.5. Найдите производную указанной функции, сначала по х, считая t постоянной, а затем по t, считая х постоянной:
1. 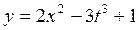
2. 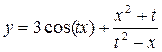
3. 
№2.6. Найти дифференциалы указанных порядков для следующих функций:
1.  , d–?
, d–?
2. 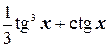 , d–?
, d–?
3. ln (ln x), d–?
4. sin 2x, d2–?
5. ecos x, d2–?
6. ex+x2, d3–?
7.  , d–?
, d–?
8. e2x, d(n)–?
№2.7. Вычислить приближенно:
1. 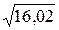 ;
;
2.  ;
;
3. 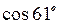 ;
;
4. 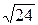 ;
;
5.  ;
;
6. ln 1,02.
Контрольные вопросы
1. Что такое приращение аргумента и приращение функции.
2. Какие значения могут они принимать?
3. Дайте определение производной функции в точке.
4. Запишите различные обозначения производной.
5. Что является биологическим смыслом производной?
6. Объясните алгебраический, физический смысл производной?
7. Объясните геометрический смысл производной.
8. Приведите примеры производной.
9. Что называется производной сложной функции?
10. Что называется производной высшего порядка?
11. Дайте понятие дифференциала функции.
12. Для всех ли функций существует дифференциал?
13. В чем состоит алгебраический смыслы дифференциала
14. В чем состоит геометрический смыслы дифференциала?
15. Докажите, что дифференциал аргумента равен его приращению.
16. Перечислите свойства дифференциала.
17. Дайте определения, в том числе в виде математического выражения, дифференциала 2-го порядка, n-го порядка.
Глава 3. Исследование функций и построение графиков
Промежутки монотонности и знакопостоянства
Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f /(x) > 0 для a < x < b, то эта функция… Аналогично можно сделать вывод о том, что если функция f(x) убывает на отрезке… Конечно, данное утверждение справедливо, если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале…Экстремумы функции
Функция f(x) имеет в точке х1 максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х1.… Очевидно, что функция, определенная на отрезке может иметь максимум и минимум… Точки максимума и минимума функции называются точками экстремума.Выпуклость и вогнутость функции. Точка перегиба
Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна (положительна), то кривая y = f(x)…Асимптоты
Прямая называется асимптотойкривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю. … Следует отметить, что не любая кривая имеет асимптоту. Асимптоты бывают…Общая схема исследования функции и построение графиков
Графики функций строятся по точкам. Обычно из уравнения y=f(x) находят несколько точек графика функции y=f(x) и соединяют эти точки плавной кривой. Однако при таком методе легко пропустить какие-то важные особенности графика и допустить ошибку в построении.
Для построения графика функции нужно исследовать ее свойства. Процесс исследования функции состоит из нескольких этапов.
1) Область определения функции.
2) Координаты точек пересечения с осями координат.
3) Четность, нечетность функции.
4) Асимптоты графика и пределы на ±∞. (Если они имеются).
5) Критические точки.
6) Интервалы монотонности и точки экстремума.
7) Промежутки выпуклости и вогнутости, точки перегиба. (Если они имеются).
8) Дополнительные точки, если нет асимптот.
9) Построение графика.
10) Область значения функции.
Примеры
№1. Исследовать функцию на монотонность и экстремум 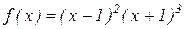 .
.
Решение.
1) D(f)=R
2) 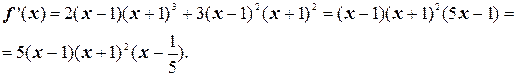
3) 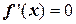 при
при  ,
,  ,
,  .
.
–1, 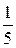 , 1 – критические точки, так как внутренние точки области определения и
, 1 – критические точки, так как внутренние точки области определения и 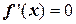 .
.
4) Выясним знаки производной:

Функция y=f(x) возрастает на промежутках (–∞; 1/5]; [1;+∞).
Функция y=f(x) убывает на промежутке [1/5; 1].
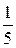 – точка максимума, f(
– точка максимума, f(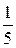 ) – максимум функции.
) – максимум функции.
1 – точка минимума, f(1) – минимум функции (рис. 3.6.1).
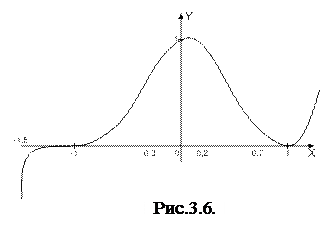 |
№2. Исследовать функцию на выпуклость и вогнутость. Найти точки перегиба: 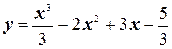 .
.
Решение.
1) D(f)=R
2)  .
.
3)  .
.
 при
при 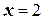 .
.

Функция y=f(x) выпуклая на промежутке (–∞; 2].
Функция y=f(x) вогнутая на промежутке [2; +∞).
(2;–1) – точка перегиба.
№3. Найти вертикальные асимптоты линии:
а) y=tgx;
б)  .
.
Решение.
а) Так как данная функция имеет разрыв в точках x=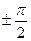 , то
, то 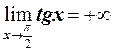 ,
,  .
.
Следовательно,  ,
, 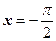 – вертикальные асимптоты.
– вертикальные асимптоты.
б) Функция 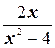 имеет бесконечный предел при х®2 и х®-2.
имеет бесконечный предел при х®2 и х®-2.
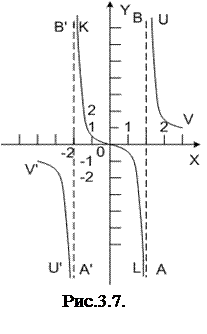 |
Значит, прямые х=2 и х= -2 (АВ и А′В′ на рис. 3.6.2) – асимптоты. Прямая АВ служит асимптотой для двух ветвей, UV и KL. Вдоль первой бесконечное удаление направлено вверх, вдоль второй – вниз (ибо  и
и 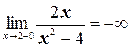 . Аналогично для прямой А′В′.
. Аналогично для прямой А′В′.
Заметим, что прямая х=0 служит горизонтальной асимптотой (для ветвей UV и U′V′).
№4.Исследовать функцию 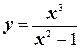 и построить ее график.
и построить ее график.
Решение.
1. Находим область определения функции: (–¥; –1) È (–1; 1) È (1; ¥).
2. Точки пересечения с осью ОХ: у=0, тогда
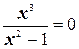 ,
,
х=0, => (0; 0) – точка пересечения с осью ОХ.
Точки пересечения с осью ОУ: х=0, тогда
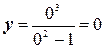 ,
,
у=0, => (0; 0) – точка пересечения с осью ОУ.
3. Область определения симметрична относительно нуля

Таким образом, функция является нечетной.
4. Так как точки х = 1, х = –1 являются точками разрыва, то вычислим следующие пределы:

Значит х = 1, х = –1 – вертикальные асимптоты.
Теперь найдем наклонные асимптоты.
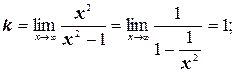

Итого, уравнение наклонной асимптоты – y = x.
5. Находим критические точки.
Найдем производную функции
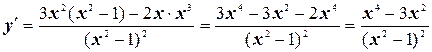
Критические точки: x = 0; x = –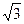 ; x =
; x = 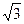 ; x = –1; x = 1.
; x = –1; x = 1.
Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
x < – , y¢ > 0, функция возрастает
, y¢ > 0, функция возрастает
– < x < –1, y¢ < 0, функция убывает
< x < –1, y¢ < 0, функция убывает
–1 < x < 0, y¢ < 0, функция убывает
0 < x < 1, y¢ < 0, функция убывает
1 < x <  , y¢ < 0, функция убывает
, y¢ < 0, функция убывает
 < x, y¢ > 0, функция возрастает
< x, y¢ > 0, функция возрастает
Видно, что точка х = – является точкой максимума, а точка х =
является точкой максимума, а точка х =  является точкой минимума. Значения функции в этих точках равны соответственно: –
является точкой минимума. Значения функции в этих точках равны соответственно: –  и
и  .
.
6. Найдем вторую производную функции
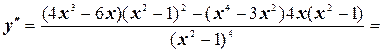
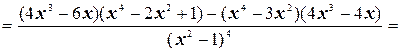
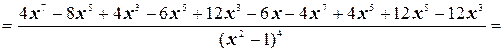
 .
.
Определим выпуклость и вогнутость кривой на промежутках.
x < –1, y¢¢ < 0, кривая выпуклая
–1 < x < 0, y¢¢ > 0, кривая вогнутая
0 < x < 1, y¢¢ < 0, кривая выпуклая
1 < x, y¢¢ > 0, кривая вогнутая
–1, 0, 1 – точки перегиба.
7. Построим график функции:


.
8. Область значения E(y)=R.
Варианты заданий
№3.1. Найти интервалы монотонности следующих функций:
1.  ;
;
2. 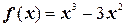 ;
;
3.  ;
;
4.  на
на  ;
;
5. 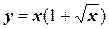 .
.
№3.7.2. Исследовать на экстремум следующие функции:
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5. 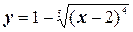 .
.
№3.3. Исследовать на выпуклость и вогнутость следующие функции:
1.  ;
;
2. 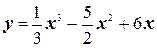 ;
;
3.  ;
;
4. 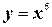 ;
;
5. 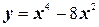 .
.
№3.4. Найти наибольшее и наименьшее значения функции:
1. 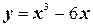 на отрезке
на отрезке  ;
;
2. 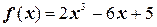 на отрезке
на отрезке  ;
;
3.  на отрезке
на отрезке  .
.
№3.5.Исследовать функции и построить их графики:
1. y=3x5–5x3+2;
2. y= ;
;
3. y= ;
;
4. y= ;
;
5. 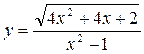
6. 
7. 
8. 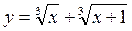
9. 
10. 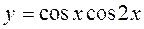
11. 
12. 
13. у = tg(x) – sin(x)
14. y = ctg(x) + cos(x)
Контрольные вопросы
1. Назовите основные пункты исследования графика функции.
2. Что называется областью определения функции?
3. Что называется областью значения функции?
4. Что является промежутками возрастания функции?
5. Что является промежутками убывания функции
6. Когда график функции имеет выпуклость?
7. Когда график функции имеет вогнутость?
8. Что называется асимптотами?
9. Какие бывают асимптоты?
10. Как найти асимптоты?
Глава 4. Функции нескольких переменных
Определение функции нескольких переменных
При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты будут… Если каждой паре независимых друг от друга чисел (х, у) из некоторого… Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то –…Частные производные
Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение Dх к переменной х. Тогда величина Dxz… Можно записать . Тогда называется частной производнойфункции z = f(x, y) по х. Обозначение:Полный дифференциал
Выражение называется полным приращениемфункции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при Dх ® 0 и Dу ® 0… Полным дифференциаломфункции z = f(x, y) называется главная линейная…Примеры
№1. Найти частные производные функций:
а)  ;
;
б) 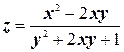 ;
;
в) 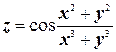 .
.
Решение.
а) Частные производные функции двух и более переменных определяются по тем же формулам и правилам, что и функции одной переменной. Следует помнить только одно правило: если по одной переменной дифференцируем, то остальные считаются постоянными.
Имеем: (напомним, что 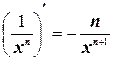 ):
):
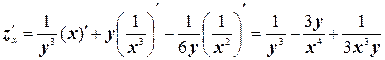 ;
;
 .
.
б) Воспользуемся правилом дифференцирования дроби:
 ;
;
 .
.
в) Здесь имеем дело с производными сложной функции и дроби.
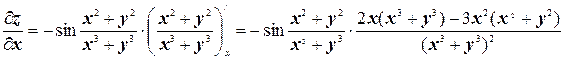 .
.
Ввиду симметрии выражения 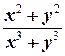 относительно х и у можно записать сразу
относительно х и у можно записать сразу
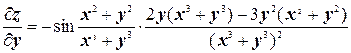 .
.
№2. Найти полный дифференциал функций:
а) 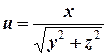 ;
;
б) 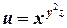 .
.
Решение.
а) Так как  , то полный дифференциал имеет вид
, то полный дифференциал имеет вид  .
.
б) Вычислим частные производные по х, у, z
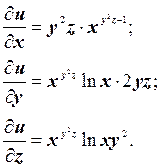
Таким образом, полный дифференциал
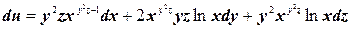
Варианты заданий
№4.1. Найти частные производные, частные дифференциалы данных функций по каждой из независимых переменных (x, y, z, t, …) и полный дифференциал:
а)  ;
;
б) 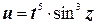 ;
;
в)  ;
;
г) 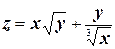 ;
;
д)  ;
;
е) 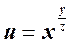 ;
;
ж) 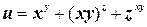 ;
;
з) 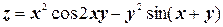 ;
;
и) 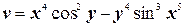 ;
;
к) 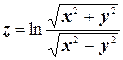 .
.
Контрольные вопросы
Глава 5. Численное дифференцирование
При анализе медицинских, инженерных и научных данных часто возникает необходимость найти наклон кривой, которая задана таблицей значений.
Возможна и другая ситуация: f(x) известна, но имеет очень сложное аналитическое выражение.
В первом случае классические методы дифференциального исчисления просто неприемлемы, а во втором случае их использование вызывает значительные трудности. В таких задачах вместо функции f(x) рассматривают интерполирующую функцию P(x), а затем полагают f '(x) » P'(x) на интервале a£x£b. Аналогично поступают при нахождении производных высших порядков функции f(x).
Если для интерполирующей функции P(x) известна погрешность интерполяции R(x)=f(x)–P(x), то погрешность производной равна производной от погрешности этой функции
r(x)=f '(x)–P'(x)=R'(x).
Такое утверждение справедливо и для производных высших порядков.
В целом же численное дифференцирование представляет собой операцию менее точную, чем интерполирование.
Формулы для вычисления первой производной
Численное дифференцирование весьма чувствительно к погрешностям, вызванным неточностью исходных данных. Значительно меньшую погрешность имеет… По трем точкам:Формулы второй производной
По четырем точкам: ; (первое значение) ; (внутренние точки) (5.4)Примеры
№1. Пользуясь безразностными формулами по 3 точкам, определить первые производные для функции у=х2 на интервале [1; 3] с шагом 0,2 и сравнить их значения с аналитическими.
Решение.
Воспользуемся формулами (5.1):



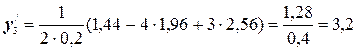
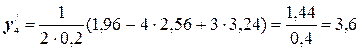

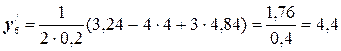
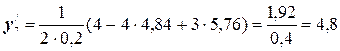

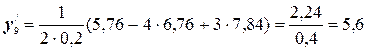

Для сравнения этих значений с аналитическими составим таблицу:
| i | хi | у=х2 | Аналитические значения у΄=2х | Численные значения у΄ |
| 1,2 1,4 1,6 1,8 2,2 2,4 2,6 2,8 | 1,44 1,96 2,56 3,24 4,84 5,76 6,76 7,84 | 2,4 2,8 3,2 3,6 4,4 4,8 5,2 5,6 | 2,0 2,4 2,8 3,2 3,6 4,4 4,8 5,2 5,6 |
Таким образом, мы видим, что все значения первой производной полностью совпадают с аналитическими.
№2. Пользуясь безразностными формулами по 4 точкам, определить первые производные для функции у=х3 на отрезке [1; 3] с шагом 0,2 и сравнить эти значения с аналитическими.
Решение.
Пользуемся формулами (5.2):
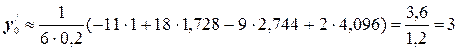

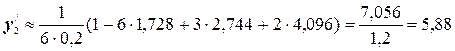
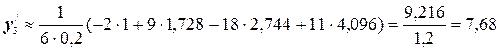 и т.д. по формуле для
и т.д. по формуле для 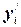 .
.
Для сравнения полученных значений с аналитическими составим таблицу:
| i | хi | у=х3 | Аналитические значения у´=3х2 | Численные значения у´(х) |
| 1,2 1,4 1,6 1,8 2,2 2,4 2,6 2,8 | 1,728 2,744 4,096 5,832 10,648 13,824 17,576 21,952 | 4,32 5,88 7,68 9,72 14,52 17,28 20,28 23,52 | 4,32 5,88 7,68 9,72 14,52 17,28 20,28 23,52 |
Получим, что для функции у=х3 численное дифференцирование по 4 точкам дает такие же значения, что и аналитические.
№3. Найти вторую производную для функции у=х3 на отрезке [1; 3] с шагом 0,2, пользуясь безразностными формулами по 4 точкам и сравнить полученные значения с аналитическими.
Решение.
Воспользуемся формулами (5.4):
 (первое значение)
(первое значение)
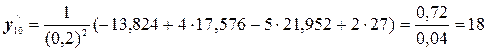 (последнее значение)
(последнее значение)

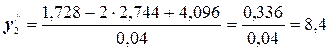 и т.д. по формуле для внутренних точек.
и т.д. по формуле для внутренних точек.
Для сравнения составим таблицу:
| i | хi | у=х3 | Аналитические значения у″=6х | Численные значения у″ |
| 1,2 1,4 1,6 1,8 2,2 2,4 2,6 2,8 | 1,728 2,744 4,096 5,832 10,648 13,824 17,576 21,952 | 7,2 8,4 9,6 10,8 13,2 14,4 15,6 16,8 | 7,2 8,4 9,6 10,8 13,2 14,4 15,6 16,8 |
Таким образом, получим, что для функции у=х3 численное нахождение второй производной по 4 точкам дает такие же значения, что и аналитические.
Варианты заданий
№ 5.1. Получить таблицы значений следующих функций на интервале от 1 до 3 с шагом 0,2. Пользуясь безразностными формулами по 4 точкам, найти численные значения первой производной в этих точках, и сравнить полученные значения с аналитическими.
1. у=ех;
2.  ;
;
3. у=ln x;
4.  ;
;
5. y=sin x;
6. y=e2x;
7. 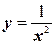 ;
;
8. у=(х–1)2;
9. y=cos x;
10. y=ln x2;
№ 5.2. Получить таблицы значений следующих функций на интервале от 1 до 3 с шагом 0,2. Пользуясь безразностными формулами по 3 точкам, найти численные значения первой производной в этих точках, и сравнить полученные значения с аналитическими.
11. у=sin x;
12. y=cos x;
13. y=sin(x2);
14. y=sin2 x;
15. y=cos2 x;
16. y=sin(2x);
17. y=cos(2x);
18. 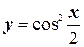 ;
;
19. y=ln2 x;
20. y=ln3 x;
№ 5.3. Для перечисленных функций, пользуясь безразностными формулами по 4 точкам, найти вторые производные в точках от 1 до 3 с шагом 0,2 и сравнить полученные значения с аналитическими.
21. y=e2x;
22. 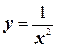 ;
;
23.  ;
;
24. у=(х–1)2;
25. y=ln(x2);
26. y= ;
;
27. y=sin2 x;
28. 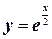 ;
;
29.  ;
;
30. 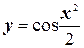 .
.
5.5. Контрольные вопросы
Глава 6 Основы интерполяции.
Постановка задачи
Пусть некоторая функция f(x) задана таблично на интервале [a,b] f(xn)=yn, f(x1)=y1, ... , f(xn)=yn (6.1)в n+1 точках x0, x1, x2, ... ,xn. Под интерполяцией понимается нахождение по таблице значений функции её аналитического описания, позволяющего вычислять…Рис. 6.1
Чтобы получить единственную f(x)наложим на неё дополнительные ограничения, а именно, в качестве f(x) используем полином P(x) степени на единицу меньше числа заданных значений n+1.
Интерполяционные формулы конечных разностей
Для функции f(x), заданной таблично, величина Di=yi+1-yi называется первой нисходящей конечной разностью. Величина D2yi=Dyi+1-Dyi - второй конечной… Dnyi=Dn-1yi+1-Dn-1yi. (6.2) Первая восходящая конечная разность определяется изИнтерполяционные формулы центральных разностей
Для функции y=f(x) заданной в равноотстоящих узлах центральные разности определяются соотношением ; ; , (6.10) которое с учётом нисходящих и восходящих разностей имеет видИнтерполирование функции с не равноотстоящими узлами
Для произвольно заданных узлов интерполяции можно воспользоваться формулой Лагранжа или многочленом Ньютона. Интерполяционный полином Лагранжа имеет… (6.14) или в развёрнутом планеПримеры
№1 Найти значение интерполирующего полинома для функции y=ex заданной таблицей.
| х | 3,50 | 3,55 | 3,60 | 3,65 | 3,70 |
| у | 33,115 | 34,813 | 36,598 | 38,475 | 40,447 |
на интервале [3,5; 3,6] с шагом =0,05.
Решение. Составим таблицу с нисходящими конечными разностями для заданных точек функции y=ex
| х | у | Δу | Δ2 у | Δ3 у |
| 3,50 3,55 3,60 3,65 3,70 | 33,115 34,813 36,598 38,475 40,447 |
Отмечаем, что значения конечных разностей третьего порядка примерно одинаковы, а это значит, что нужно использовать полином Pn(x) степени n=3. Для х0=3,50 и у0=33,115, мы имеем отыскиваемый полином в виде.
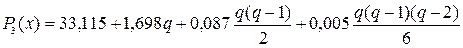
или с учетом значений
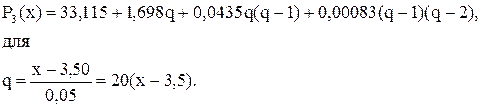
№2 Необходимо найти значение функции y(x) для x1=1,2173 по данным таблицы.
| x | y |
| 1.215 1.220 1.225 1.230 1.235 1.240 1.245 1.250 1.255 1.260 | 0.106044 0.106491 0.106935 0.107377 0.107818 0.108257 0.108696 0.109134 0.109571 0.110008 |
Найдем для этого случая нисходящие конечные разности.
| i | xi | yi | Δуi | Δ2 уi |
| 1.215 1.220 1.225 1.230 1.235 1.240 1.245 1.250 1.255 1.260 | 0.106044 0.106491 0.106935 0.107377 0.107818 0.108257 0.108696 0.109134 0.109571 0.110008 | 0.000447 0.000444 0.000442 0.000441 0.000439 0.000439 0.000438 0.000437 0.000437 - | -0.000003 -0.000002 -0.000001 -0.000002 -0.000001 -0.000001 - - |
Отметим, что, начиная со второго порядка, конечные разности примерно одинаковы. Следовательно, воспользуемся полиномом Ньютона второго порядка, для x=1,2173.


№3 Пусть yx функция заданная таблицей с неравноотстоящими значениями аргумента.
| x | y |
| 0,103 0,108 0,115 0,120 0,128 0,136 0,141 0,150 | 2,01284 2,03342 2,06070 2,07918 2,10721 2,13354 2,14922 2,17609 |
Нужно вычислить значение функции для x1=0,112.
Воспользуемся формулой Лагранжа
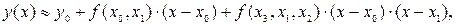
где используются разделенные разности.
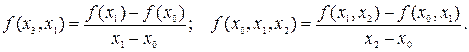
Составим таблицу этих разностей.
| xi | yi | f(xi,xi+1) | f(xi,xi+1,xi+2) |
| 0,103 0,108 0,115 0,120 0,128 0,136 0,141 | 2,01284 2,03342 2,06070 2,07918 2,10721 2,13354 2,14922 | 4,116 3,896142 3,696 3,503750 3,291250 3,136 - | -18,238166 -16,761833 -14,788461 -13,281250 -11,942307 - - |
Затем определяем f(0,112) двумя методами, для x0 равным соответственно 0,103 и 0,108:

 В результате имеем f(0,112) ≈ 2,04922.
В результате имеем f(0,112) ≈ 2,04922.
№4 Оттискать эмпирическую формулу для функции yx заданной таблично.
| X | ||||||
| y | 5.2 | 8.0 | 10.4 | 12.4 | 14.0 | 15.2 |
Вычислим нисходящие конечные разности второго порядка
| x | y | Δy | Δ2 y |
| 5.2 8.0 10.4 12.4 14.0 15.2 | 2.8 2.4 2.0 1.6 1.2 | -0.4 -0.4 -0.4 -0.4 |
из таблицы видим, что  , а это значит необходим полином Ньютона второй степени. Запишем его в виде
, а это значит необходим полином Ньютона второй степени. Запишем его в виде
y = 5,2 + 2,8x – 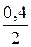 x(x – 1)
x(x – 1)
в итоге имеем
y = 5,2 + 3x – 0,2x2.
№5 Пусть yxзаданнасвоими значенияи в нижеприведенной таблице. Необходимо вычислить значение yxдля аргумента x=0,304, используя полиномы Ньютона первого и второго порядков.
| x | y |
| 0,29 | 3,25 |
| 0,30 | 3,17 |
| 0,31 | 3,12 |
| 0,32 | 3,04 |
| 0,33 | 2,98 |
| 0,34 | 2,91 |
Полином Ньютона первого порядка
y(0,304) = y0 + q∙Δy0;
h(x) = x1- x0 = 0,31-0,30 = 0,01.
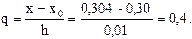
Δy0 = y1- y0 = 3,12 - 3,17 = -0,05.
y(0,304) = 3,17 + 0,4 ∙ (-0,05) ;
y(0,304) = 3,15.
Полином Ньютона второго порядка

Δ2y0 = Δ1y1 – Δ1y0 = 3,04 – 3,12 – (-0,05) = -0,03.

y(0,304) = 3,153.
Варианты заданий
6.1. Найти значение функции, используя формулу Лагранжа по данным таблицы
Таблица 1
| х | у | Вариант № | х | |
| 0,43 0,48 0,55 0,62 0,70 0,75 | 1,63597 1,73234 1,87686 2,03345 2,22846 2,35973 | 0,702 0,512 0,645 0,736 0,608 |
Таблица 2
| х | y | Вариант № | х | |
| 0,02 0,08 0,12 0,17 0,23 0,30 | 1,02316 1,09590 1,14725 1,21483 1,30120 1,40976 | 0,102 0,114 0,125 0,203 0,154 |
6.2. Найти значения функции, используя полиномы Ньютона для начала и конца интервала интерполяции.
Таблица 3
| х | у | Вариант № | х | |
| 1,375 1,380 1,385 1,390 1,395 1,400 | 5,04192 5,17744 5,32016 5,47069 5,62968 5,79788 | 1,3832 1,3926 1,3862 1,3934 1,3866 |
Таблица 4
| х | у | Вариант № | х | |
| 0,115 0,120 0,125 0,130 0,135 0,140 | 8,65729 8,29329 7,95829 7,64893 7,36235 7,09613 | 0,1264 0,1315 0,1232 0,1334 0,1285 |
Таблица 5
| х | y | Вариант № | х | |
| 0,150 0,155 0,160 0,165 0,170 0,175 | 6,61659 6,39989 6,19658 6,00551 5,82558 5,65583 | 0,1521 0,1611 0,1662 0,1542 0,1625 |
Контрольные вопросы
Глава 7. Неопределенный интеграл
Первообразная функция и неопределенный интеграл
Пусть функция f(x) определена на некотором (конечном или бесконечном) интервале (а; b). Функция F(x) называется первообразной для функции f(x) на… для всех или dF(x)= f(x)dx. функция 3x2 есть производная от x3, т. е. 3x2dx есть дифференциал функции x3:Основные свойства неопределенного интеграла
1. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная: . 2. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла…Таблица простейших интегралов
1. 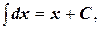
2. 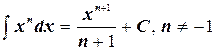
3. 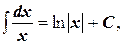
4. 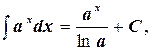
5. 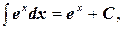
6. 
7. 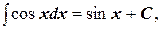
8. 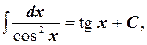
9. 
10. 
11. 
12. 
13. 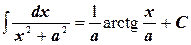 ,
,
14. 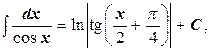
15. 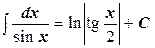 ,
,
16. 
17. 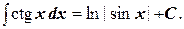
Основные методы интегрирования
Способ непосредственного интегрирования основан на использовании свойств неопределенного интеграла и приведении подынтегрального выражения к… Пример. Найти интегралы: 1) .Примеры
№1.Найти интегралы непосредственным интегрированием:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
Решение.
а) Почленно поделив числитель подынтегральной дроби на знаменатель, будем иметь
 .
.
Тогда 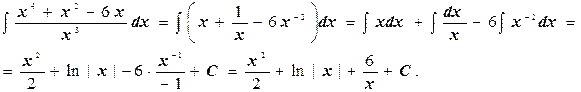
б) Воспользуемся свойствами 3 и 4 неопределенного интеграла, тем самым сводя исходный интеграл к сумме табличных интегралов:

в) 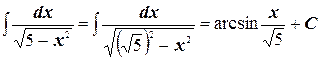
г)  .
.
Здесь мы воспользовались свойством 5 неопределенного интеграла и формулой 4 пункта 7.3.
№2.Найти интегралы методом подстановки:
а) 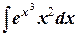 ;
;
б) 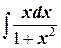 ;
;
в) 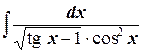 ;
;
г)  .
.
Решение.
а) 
б) 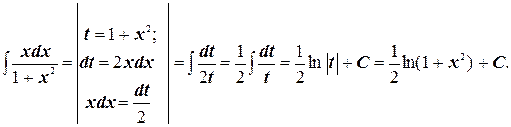
в) 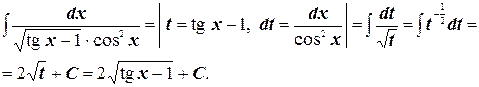
г) 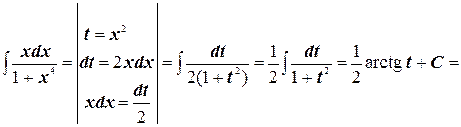

№3.Найти интегралы с помощью метода интегрирования по частям:
а) 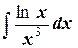 ;
;
б) 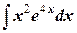 .
.
Решение.
а) Положим 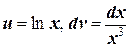 , откуда
, откуда  . Тогда по формуле (6.4.1) находим
. Тогда по формуле (6.4.1) находим
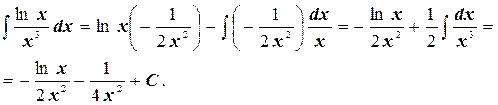
б)  (*)
(*)
К последнему интегралу снова применим формулу интегрирования по частям. Положим  , тогда
, тогда  , следовательно,
, следовательно,

Подставляя найденное выражение в соотношение (*), получим
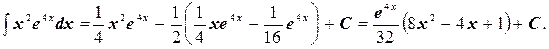
Варианты заданий
№7.1. Найти интегралы непосредственным интегрированием:
а) 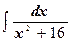 ;
;
б) 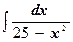 ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  ;
;
ж)
з)  ;
;
и) 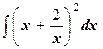 ;
;
к) 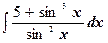 ;
;
л) 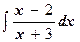 ;
;
м)  .
.
№7.2. Найти интегралы методом подстановки:
а) 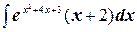 ;
;
б)  ;
;
в) 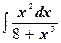 ;
;
г) 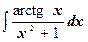 ;
;
д)  ;
;
е) 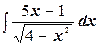 ;
;
ж) 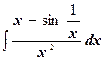 ;
;
з) 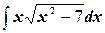 ;
;
и) 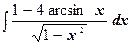 ;
;
к) 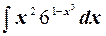 ;
;
л)  ;
;
м) 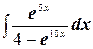 .
.
№7.3. Найти интегралы с помощью метода интегрирования по частям:
а) 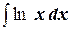 ;
;
б)  ;
;
в)  ;
;
г) 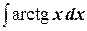 ;
;
д) 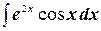 ;
;
е)  ;
;
ж) 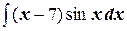 ;
;
з)  ;
;
и)  ;
;
к)  .
.
Контрольные вопросы
1. Что такое первообразная? Обладают ли первообразные одной функции свойством единственности?
2. Дайте определение, в том числе виде математического выражения, неопределенного интеграла.
3. Что такое подынтегральная функция? Подынтегральное выражение?
4. Перечислите основные свойства неопределенного интеграла. Запишите эти свойства в виде математических выражений.
5. Воспроизведите таблицу основных интегралов. Докажите справедливость записанных выражений с использованием операции дифференцирования.
6. В чем заключается метод замены переменной в определенном интеграле? метод интегрирования по частям?
7. Какие функции в подынтегральном выражении рекомендуется выбирать в качестве и и dv при интегрировании по частям?
8. Назовите основные типы интегралов, к которым применяется метод интегрирования по частям.
9. Что называется рациональной дробью? Как выделить из неправильной рациональной дроби и правильную дробь? Как разложить правильную дробь на сумму простейших?
Глава 8. Определенный интеграл
Основные понятия и свойства определенного интеграла
Пусть функция f(x) определена на отрезке [a; b]. Разобьем отрезок [a; b] на n частей точками a=x0<x1<…<xn–1<xn=b; на каждом элементарном отрезке [xk–1, xk] выберем произвольную точку ck и обозначим через  длину каждого такого отрезка. Вычислим значения функции f(x) в точках ck, где k={1, 2, …, n}.
длину каждого такого отрезка. Вычислим значения функции f(x) в точках ck, где k={1, 2, …, n}.
Интегральной суммой для функции f(x) на отрезке [a; b] называется сумма вида
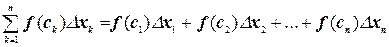 (7.1.1)
(7.1.1)
Определенным интегралом от функции f(x) на отрезке [a; b] называется предел интегральной суммы (7.1.1), при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
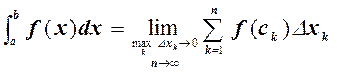 (7.1.2)
(7.1.2)
При этом f(x) называется подынтегральной функцией, x – переменной интегрирования, числа а и b – соответственно нижним и верхним пределами интегрирования, [a; b] – промежутком интегрирования.
Свойства определенного интеграла
2. 3. Определенный интеграл от суммы конечного числа непрерывных функций f1(x), f2(x), …, fn(x), заданных на отрезке [a;…Основные методы интегрирования
Для вычисления определенного интеграла от непрерывной на отрезке [a;b]функции f(x) в том случае, когда может быть найдена ее первообразная F(x)… , т.е. определенный интеграл равен разности значений любой первообразной при верхнем и нижнем пределах интегрирования. …Примеры
№1. Используя формулу Ньютона-Лейбница, найти интегралы:
а)  ;
;
б)  ;
;
в)  ;
;
г) 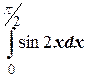 .
.
Решение.
а) Для нахождения первообразной проведем преобразования, чтобы получить табличный интеграл (в подкоренном выражении выделим полный квадрат):

б) 

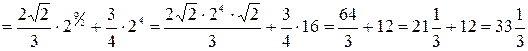 .
.
в) 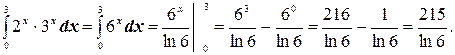
г) 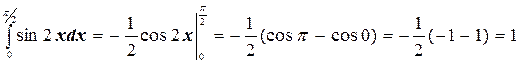 .
.
№2. Вычислить интегралы методом подстановки:
а) 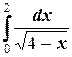 ;
;
б) 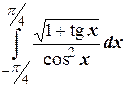 ;
;
в)  ;
;
г)  .
.
Решение.
а) 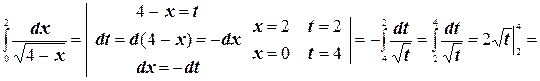

б) 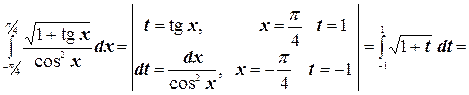
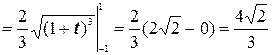
в) 

г) 
 .
.
№3. Вычислить интегралы, применяя формулу интегрирования по частям:
а)  ;
;
б)  .
.
Решение.
а) 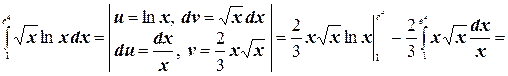


б) 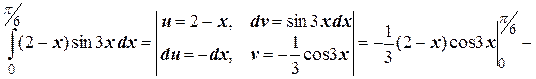


Варианты заданий
№8.1. Вычислить интегралы по формуле Ньютона-Лейбница:
а) 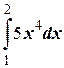 ;
;
б) 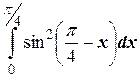 ;
;
в)  ;
;
г) 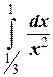 ;
;
д)  ;
;
е)  ;
;
ж)  ;
;
з) 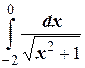 ;
;
и) 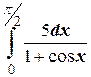 ;
;
к) 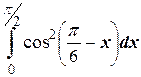 ;
;
л)  ;
;
м)  ;
;
н)  ;
;
о)  .
.
№8.2. Вычислить интегралы методом подстановки:
а)  ;
;
б) 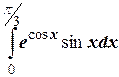 ;
;
в)  ;
;
г) 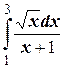 ;
;
д) 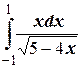 ;
;
е)  ;
;
ж) 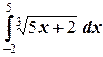 ;
;
з)  ;
;
и)  .
.
№8.3. Вычислить интегралы интегрированием по частям:
а) 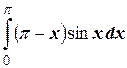 ;
;
б) 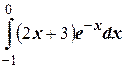 ;
;
в) 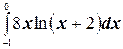 ;
;
г)  ;
;
д)  ;
;
е) 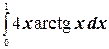 ;
;
ж) 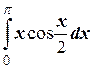 ;
;
з) 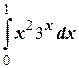 ;
;
и)  ;
;
к)  .
.
Биологические, физические и медицинские приложения определенного интеграла
8.5.1. Примеры задач прикладного характера.
Будем считать численность популяции, биомассу популяции и т.п. непрерывными функциями времени.
1. Численность популяции. Число особей в популяции (численность популяции) меняется со временем. Если условия существования популяции благоприятны, то рождаемость превышает смертность, и общее число особей популяции растет со временем. Назовем скоростью роста популяции прирост числа особей в единицу времени. Обозначим эту скорость V(t). В “старых”, установившихся популяциях, давно обитающих в данной местности, скорость роста мала и медленно стремятся к нулю. Однако если популяция молода, ее взаимоотношения с другими местными популяциями еще не установились, или существуют внешние причины, изменяющие эти взаимоотношения (например, сознательное вмешательство человека), то V(t) может значительно колебаться, уменьшаясь или увеличиваясь.
Если известна скорость роста популяции, то мы можем найти прирост численности за промежуток времени от t1 до t2. В самом деле, из определения V(t) следует, что она является производной от численности N(t) в момент t, и, следовательно, численность N(t) является первообразной для V(t). Отсюда
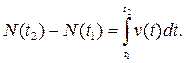 (8.1)
(8.1)
Так, известно, что в условиях неограниченных ресурсов питания скорость роста многих популяций экспоненциальна: V(t)=aert. Популяция в этом случае как бы “не стареет”. Такие условия можно создать, например, для микроорганизмов, пересаживая время от времени развившуюся культуру в новые емкости с питательной средой. В этом случае получим
 (8.2)
(8.2)
По формуле, подобной (8.2), подсчитывают, в частности, численность культивируемых плесневых грибков, выделяющих пенициллин.
2. Биомасса популяции. Рассмотрим популяцию, в которой вес особи заметно меняется в течение жизни, и подсчитаем общую биомассу популяции.
Пусть t означает возраст в тех или иных единицах времени, а N(t) – число особей популяции, возраст которых равен t. Пусть, наконец Р(t) – средний вес особи возраста t, а М(t) – биомасса всех особей в возрасте от 0 до t.
Заметим, что произведение N(t)P(t) равно биомассе всех особей возраста t, и рассмотрим разность М(t+Dt)-М(t). Очевидно, что эта разность, равная биомассе всех особей в возрасте от t до t+Dt, удовлетворяет неравенствам
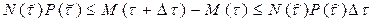 (8.3)
(8.3)
где N( )P(
)P( ) – наименьшее, а N(
) – наименьшее, а N(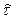 )P(
)P(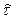 ) – наибольшее значения функции N(t)P(t) в промежутке [t,t+Dt].
) – наибольшее значения функции N(t)P(t) в промежутке [t,t+Dt].
Поэтому можно записать, что

где Т – максимальный возраст особи в данной популяции. Так как М(0), очевидно, равна нулю, то окончательно получаем
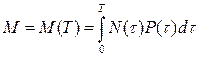
1. Средняя длина полета. В некоторых исследованиях необходимо знать среднюю длину пробега, или среднюю длину пути при прохождении животным некоторого фиксированного участка. Мы приведем соответствующий расчет для птиц. Пусть участком будет круг радиуса R. Будем считать, что R не слишком велико, так что большинство птиц изучаемого вида пересекают этот круг по прямой.
Птица может под любым углом в любой точке пересечь окружность. В зависимости от этого длина ее пролета над кругом может быть равной любой величине от 0 до 2R. Нас интересует средняя длина пролета. Обозначим ее l.
Так как круг симметричен относительно любого своего диаметра, нам достаточно ограничится теми птицами, которые летят в каком-нибудь одном направлении (например, в направлении, параллельном оси Оу). Тогда средняя длина пролета – это просто среднее расстояние между дугами АСВ и АС1В. Иными словами, это среднее значение функции f1(x)-f2(x), где y=f1(x) – уравнение верхней дуги, а y=f2(x) – уравнение нижней дуги, т.е.
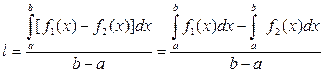 (8.4)
(8.4)

|
 равен
равен
 площади криволинейной трапеции aACBb, а
площади криволинейной трапеции aACBb, а 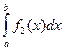 равен площади трапеции aAC1Bb, то их разность равна площади круга, т.е. pR2. Разность b-a равна, очевидно 2R. Подставив это в (8.4), получим
равен площади трапеции aAC1Bb, то их разность равна площади круга, т.е. pR2. Разность b-a равна, очевидно 2R. Подставив это в (8.4), получим
|

8.5.2. Примеры решения задач.
№1. В условиях неограниченных ресурсов питания скорость u(t)= роста многих популяций экспоненциальна, т. е.
роста многих популяций экспоненциальна, т. е.  u(t)=aekt. Найти прирост Dn популяции за время Dt=t2-t1.
u(t)=aekt. Найти прирост Dn популяции за время Dt=t2-t1.
Решение: Так как u= , то dn= u(t)dt, откуда Dn=
, то dn= u(t)dt, откуда Dn=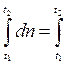 u(t)dt или Dn=n(t2)-n(t1)=n(t)
u(t)dt или Dn=n(t2)-n(t1)=n(t)
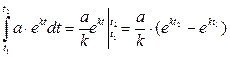

№2. Расстояние пружины x пропорционально приложенной силе –F (закон Гука): F=kx. Вычислить работу силы F при растяжении пружины на 5 см ( 0,05м), если k=200 (Н/м).
Решение: На основании формулы работы имеем:
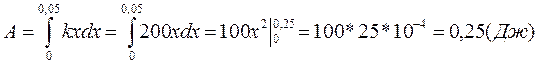
№3. 100 г. двуокиси углерода нагревается при постоянном объёме от 105° до 1000° С. Определить количество поглощаемой при этом теплоты, если теплоёмкость сv=A(B+Dt) Дж/моль*град, где A=4,19; B=6,5; D=0,00193.
Решение. Количество теплоты, поглощаемой при повышении температуры от t1 до t2, для одного моля выражается формулой

В нашей задаче число молей CO2 равно 100/44.
Q=
№4. Найти энергию связи между ионами в отдельной молекуле хлорида калия (KCl), если постоянная решетки KCl r=2,79 (1
(1 =10-8см) и связь между атомами в молекуле KCl электростатическая. Заряд иона e=4,803*10-10 ед. CGSE.
=10-8см) и связь между атомами в молекуле KCl электростатическая. Заряд иона e=4,803*10-10 ед. CGSE.
Решение. Энергия связи равна работе по перемещению иона из бесконечности до расстояния, равного постоянной решетки. Сила взаимодействия между ионами подчиняется закону Кулона и для любого расстояния x равна F(x)=e2/x2. Энергия связи
E=A= эрг.
эрг.
8.5.3. Варианты заданий
1) При прохождении электрического тока по нервному волокну оно возбуждает при условии, что проходящий ток больше рогового. Предполагается, что возбуждающий ток увеличивает величину параметра состояния e, называемого «электрическим возбуждением». Как только e превышает определенное значение e0, возникает возбуждение. Скорость изменения e зависит от тока i:
 .
.
Определить связь между параметром e и i при условии, что на нервную ткань воздействуют с постоянным током.
2) Найти путь S, пройденный материальной точкой от начала движения (t=0) до её остановки, зная скорость V(t) её прямолинейного движения: V(t)= 18t - 6t2 (м/с).
3) Два электрических заряда q1=1 Кл и q2=1,2 Кл находятся в воздухе (e=1) на расстоянии x1= 0,2 м. Какую работу надо затратить, чтобы сблизить заряды до расстояния x2=0,05 м.
4) Получит общее выражение для работы, совершенной  молями идеального газа при изотермическом расширении от V1 до V2.
молями идеального газа при изотермическом расширении от V1 до V2.
5) Скорость изменения в крови концентрации C препарата с изотопным индикатором зависит от времени q ни t (час) по закону:
а)  б)
б) 
Найти концентрацию препарата в крови через t=4 часа, если начальная концентрация  .
.
6) Вычислить работу переменного тока J=J0sin wt за период T (за время t1=0 до t2 =T) при прохождении его через проводник с сопротивлением R (v- круговая частота, v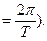

7) Воздух содержит a=8% CO2; он пропускается через цилиндрический сосуд с поглотительной массой. Тонкий слой массы поглощает количество газа, пропорциональное его концентрации и толщине слоя.
а) Если воздух, прошедший слой в H = 10 см толщиной, содержит b=2% CO2, то какой толщины должен быть поглотительный слой, для того чтобы, выходя из поглотителя, воздух содержался C = 1% CO2 углекислоты?
б) Сколько углекислоты (d%) останется в воздухе, прошедшем поглотитель, если толщина поглотительного слоя будет равна 30 см?
8) Если при прохождении через слой воды толщиной x1 =3м поглощается половина первоначального количества света, то какая часть этого количества дойдёт до глубины x2 = 30 м. (Количество света dJ, поглощенного тонким слоем воды, пропорционально толщине dx слоя и количеству света J, падающего на поверхность его - dJ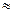 Jdx ).
Jdx ).
9) Если первоначальное количество фермента 1 г через час становится равным 1,2 г, то чему оно будет равно через 5 часов после начала брожения, если считать, что скорость прироста фермента пропорциональна его начальному количеству?
10) Найти функцию, производная от которой равна sinx +2cosx и при x=p принимает значение, равное 4.
11) Найти уравнение кривой, проходящей через точку А(2; 1), зная, что наклон касательной к кривой в каждой её точке равен x.
12) Найти функцию обращающуюся в 2e при x=1, если производная от этой функции равна 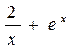 .
.
13) Скорость тела задана формулой u=(6t2+2t)м/с. Найти уравнение пути s, если за t = 3 с тело прошло путь s=60 м.
14) Скорость точки задана уравнением u=(t2-2t+5)м/с. Найти уравнение движения точки, если в начальный момент времени она находится в начале координат.
15) Скорость движущейся точки дана уравнением u = 2et м/с. В момент t = 1 с точка находится на расстоянии s = 3e м от начала отсчета. Найти закон движения точки.
16) Тело, брошенное вертикально вверх, имело начальную скорость u0=73,5 м/с. Пренебрегая сопротивлением воздуха, найти, через сколько секунд оно достигнет наибольшей высоты.
17) 100 г. двуокиси углерода нагревается при постоянном объёме от 105° до 900° С. Определить количество поглощаемой при этом теплоты, если теплоёмкость сv=A(B+Dt) Дж/моль*град. где A=4,24; B=7,5; D=0,00215.
18) Скорость движения тела выражена формулой v=(3t2-2t) м/с. Какой путь пройдёт тело за 5 с от начала движения?
19) Найти работу, произведённую при сжатии пружины на 3 см, если известно что сжатия её 0,5 см нужно приложить силу в 10 Н.
20) В цилиндре с подвижным поршнем заключен атмосферный воздух. Объём цилиндра равен 0,2 м3. Поршнем воздух сжимается до объёма 0,06 м3. Найти работу, произведенную силой давления воздуха, если температура воздуха поддерживается постоянной.
21) Тело движется в некоторой среде прямолинейно по закону s=t2. Сопротивление среды пропорционально квадрату скорости движения. Найти работу, произведенную силой сопротивления среды, при передвижении тела от s=0 до s=a.
22) Вычислить работу, затрачиваемую спортсменом при растяжении пружины эспандера на 70 см, если известно, что при усилии в 10 Н эспандер растягивается на 1 см.
23) Два электрических заряда: q1=100 ед. CGSE и q2=120 ед. CGSE находятся в воздухе на расстоянии 20 см друг от друга. Каким будет расстояние между зарядами, если приблизить второй к первому, затратив при этом работу в 1800 эрг?
24) Вычислить работу тока за время от t1=0 до t2=T, если сила тока определяется формулой I=I0 sin w0t, где I0- максимальное значение тока; w0- круговая частота; t- время.
25) Формула температурной зависимости истинной мольной теплоёмкости Fe2O3:
cr= A (B+CT-DT2) кал/моль*град.
Где A=4,19; B=24,72; C=16,04; D=4,234. Определить количество теплоты (в кДж), необходимое для нагревания 1 кг Fe2O3 от 16° до 1538° С.
26) На расстоянии x находятся два тела массами m1 и m2, которые взаимодействуют друг с другом с силой F=y
находятся два тела массами m1 и m2, которые взаимодействуют друг с другом с силой F=y . Вычислить работу, которую производит эта сила при перемещении тела m2 в бесконечность из положения x=a.
. Вычислить работу, которую производит эта сила при перемещении тела m2 в бесконечность из положения x=a.
27) Найти среднее значение электродвижущей силы Eср, изменяющейся со временем по закону E=E0sin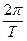 t, и среднее значение её квадрата E2ср в течение одного полупериода, т. е. от t=0 до t=T/2.
t, и среднее значение её квадрата E2ср в течение одного полупериода, т. е. от t=0 до t=T/2.
28) Найти массу стержня длинной 0,50 см, если линейная плотность стержня меняется по закону r=(5x+0,4x2) кг/м, где x – расстояние от одного из концов стержня.
29) Найти количество тепла, выделяемое переменным синусоидальным током I=2sin в течение периода T=0,02 с в проводнике с сопротивлением 100 Ом.
в течение периода T=0,02 с в проводнике с сопротивлением 100 Ом.
30) Некоторая масса газа при давлении 104 Н/м2 занимает объём 4 м3. Какую работу надо совершить над газом, чтобы, не изменяя его температуры, уменьшить объём до 1 м3?
8.6. Контрольные вопросы
1. Дайте понятие интегральной суммы.
2. Что называется определенным интегралом?
3. Запишите формулу Ньютона-Лейбница.
4. Перечислите основные свойства определенного интеграла. Сформулируйте теорему о среднем.
5. Каковы характерные особенности применения метода замены переменной к вычислению определенного интеграла?
6. Каковы характерные особенности применения метода интегрирования по частям к вычислению определенного интеграла?
7. В чем состоит геометрический смысл определенного интеграла?
8. Приведите примеры применения интегрального исчисления в биологии и медицине.
Глава 9. Численное интегрирование
Существует огромное количество функций, интеграл от которых не может быть выражен через элементарные функции. Для нахождения интегралов от подобных функций применяются разнообразные приближенные методы, суть которых заключается в том, что подынтегральная функция заменяется «близкой» к ней функцией, интеграл от которой выражается через элементарные функции.
Формула прямоугольников
Если известны значения функции f(x) в некоторых точках x0, x1, … , xm, то в качестве функции «близкой» к f(x) можно взять многочлен Р(х) степени не… Разобьем отрезок интегрирования [a; b] на n равных частей. Обозначим длину каждой части. При этом y0 = f(x0), y1 =…Формула трапеций
Эта формула является более точной по сравнению с формулой прямоугольников. Подынтегральная функция в этом случае заменяется на вписанную ломаную. … Геометрически площадь криволинейной трапеции заменяется суммой площадей… Площади вписанных трапеций вычисляются по формулам:Метод средних
Пусть для определенности a = x0, b = xn. Обозначим через , , , … середины интервалов (x0, x1), (x1, x2), (x2, x3), … Полагаем f() = , f() = , f() =,… (9.3) Выражение (9.3)определяет площадь ступенчатой фигуры (риc. 8.3.1).Формула Симпсона
Разделим отрезок интегрирования [a, b] на четное число отрезков п=2m. Площадь… Для каждой пары отрезков построим такую параболу (рис. 8.4.1).Примеры
№1. Найти приближенное значение определенного интеграла  с помощью формулы Симпсона и формулы трапеций, разбив отрезок интегрирования на 10 частей.
с помощью формулы Симпсона и формулы трапеций, разбив отрезок интегрирования на 10 частей.
Решение.
Так как п=2т, то в нашем примере т=5. По формуле Симпсона получим:

Все дальнейшие расчеты приведены в таблице:
| i | |||||||||||
| xi | –2 | –1 | |||||||||
| y(xi) | 2,83 | 3,87 | 4,12 | 4,9 | 6,56 | 8,94 | 11,87 | 15,23 | 18,95 | 22,98 |
Окончательно получим,

Точное значение этого интеграла – 91.173.
Как видно, даже при сравнительно большом шаге разбиения точность полученного результата вполне удовлетворительная.
Абсолютная погрешность равна  .
.
Относительная погрешность 
Для сравнения применим к этому же интегралу формулу трапеций.
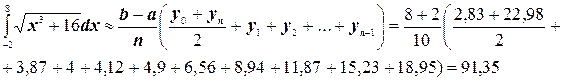
Абсолютная погрешность равна 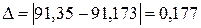 .
.
Относительная погрешность 
Формула трапеций дала менее точный результат по сравнению с формулой Симпсона.
№2. Вычислить определенный интеграл 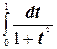 с помощью формулы прямоугольников, если п=10.
с помощью формулы прямоугольников, если п=10.
Решение.
По формуле прямоугольников получим:  .
.
Резльтаты вычислений поместим в таблицу:
| i | ||||||||||
| ti | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| y(ti) | 0,99 | 0,96 | 0,92 | 0,86 | 0,80 | 0,74 | 0,67 | 0,61 | 0,55 |
Таким образом,
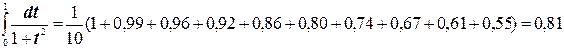 .Точное значение этого интеграла – 0,79.
.Точное значение этого интеграла – 0,79.
Найдем точное значение интеграла

Абсолютная погрешность равна 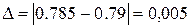 .
.
Относительная погрешность 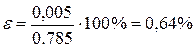
Вывод: формула прямоугольников для данного числа разбиений дала достаточно точный результат (погрешность меньше 1%).
№3. Найти площадь криволинейной трапеции, ограниченной графиком функции y =  и прямыми: y = 0, x = a = 1, x = b =11 методами:
и прямыми: y = 0, x = a = 1, x = b =11 методами:
а) прямоугольников;
б) трапеций;
в) Симпсона;
г) аналитическим с использованием формулы Ньютона-Лейбница.
Построить график заданной функции с разбиением отрезка 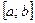 на n = 10 подынтервалов и график функции
на n = 10 подынтервалов и график функции  на отрезке x
на отрезке x
 .
.
Решение. Составим таблицу разбиения отрезка интегрирования на n = 10 равных участков с длинами интервалов Dx =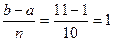 (табл. 11.1). Во второй строке таблицы представлены увеличенные в 10 раз значения
(табл. 11.1). Во второй строке таблицы представлены увеличенные в 10 раз значения  (k =
(k =  ).
).
Таблица 9.1 Данные для численных методов
 
| 1 2 3 4 5 6 7 8 9 10 11 |

| 10 7,07 5,77 5,00 4,47 4,08 3,78 3,54 3,33 3,16 3,02 |
а) Используя формулу прямоугольников с высотами, представляющими собой левые значения функции на концах подынтервалов, найдем приближенное значение площади криволинейной трапеции в виде суммы площадей прямоугольников, очерченных на рис. 11.6 сплошными линиями:

Та же формула прямоугольников, но с подстановкой в нее высот, равных правым значениям функции на концах подынтервалов, дает значение интеграла, равного площади ограниченных пунктиром прямоугольников:
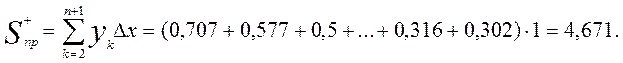
б) По формуле трапеции получим

Следует обратить внимание на очевидное равенство

в) По формуле Симпсона (n=5–количество спаренных подынтервалов)

г) Определим точное значение интеграла, являющегося табличным:
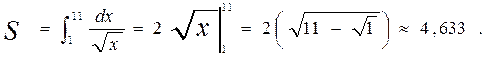
Найдем относительные ошибки определения площадей различными использованными методами численного интегрирования, сравнивая их с точным значением площади, полученным по формулам Ньютона-Лейбница:

Аналогично:

 ;
; 
Варианты заданий
Для всех вариантов выполнить:
а). С помощью формул прямоугольников, трапеций и Симпсона вычислить интегралы при заданном числе разбиений.
б). Сравнить полученные результаты с точными значениями интегралов, найденными аналитически. Для каждого метода рассчитать значения абсолютной (D) и относительной (e) погрешностей вычислений.
Используемые формулы: 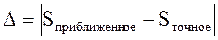

в). Сделать выводы о точности полученных результатов.
2.  ;
;
3. 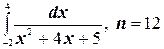 ;
;
4.  ;
;
5. 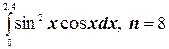 ;
;
6. 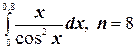 ;
;
7. 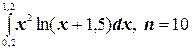 ;
;
8. 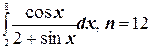 ;
;
9. 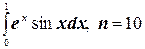 ;
;
10.  ;
;
11. 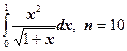 ;
;
12.  ;
;
13.  ;
;
14.  ;
;
15.  .
.
Контрольные вопросы
1. Что такое первообразная? Обладают ли первообразные одной функции свойством единственности?
2. Дайте определение, в том числе в виде математического выражения, неопределенного интеграла.
3. Что такое подынтегральная функция? подынтегральное выражение?
4. В чем заключается метод замены переменной в определенном интеграле? Метод интегрирования по частям?
5. Что называется определенным интегралом?
6. Запишите формулу Ньютона-Лейбница.
7. В чем состоит геометрический смысл определенного интеграла? экономический смысл?
8. В чем суть применения метода прямоугольников при вычислении определенных интегралов? метода трапеций?
9. Какая аппроксимация подынтегральной функции осуществляется при выводе формулы Симпсона.
10. Могут ли результаты вычисления определенных интегралов по формулам трапеций или прямоугольников быть точнее результатов, полученных по формуле Симпсона?
Глава 10. Дифференциальные уравнения
Основные определения
Символически дифференциальное уравнение можно записать так: (10.1) Дифференциальное уравнение называется обыкновенным, если искомая функция y=f(x) зависит от одного независимого…Уравнения с разделяющимися переменными
Дифференциальное уравнение вида
 , (10.3)
, (10.3)
в котором коэффициенты при дифференциалах распадаются на произведение множителей, каждый из которых зависит только от x или только от y, называется уравнением с разделяющимися переменными.
Поделив обе части уравнения (10.3) на 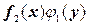 , получим уравнение
, получим уравнение
 ,
,
в котором переменные разделены. Почленное интегрирование последнего уравнения приводит к соотношению
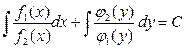 , (10.4)
, (10.4)
где С – постоянная интегрирования. Выражение (10.4) является общим решением (общим интегралом, поскольку решение записано в неявном виде) уравнения (10.3). Выражая y из (10.4) (если это возможно), получаем общее решение дифференциального уравнения в явном виде y=φ(x, C).
Заметим, что уравнению (10.3) могут удовлетворять решения, потерянные при делении на 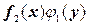 , т.е. получаемые из уравнения
, т.е. получаемые из уравнения 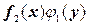 =0. Если эти решения не входят в найденный общий интеграл, то они являются особыми решениями уравнения (10.3).
=0. Если эти решения не входят в найденный общий интеграл, то они являются особыми решениями уравнения (10.3).
Частное решение находим, используя начальные условия  .
.
Кроме того, для получения решения дифференциального уравнения (10.3), удовлетворяющего произвольному начальному условию y(x0)=y0, можно воспользоваться равенством 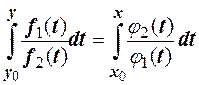 .
.
Однородные уравнения первого порядка
Например, f(x,y)=– однородные функции соответственно первой, нулевой и четвертой степени. Дифференциальное уравнение вида P(x, y)dx+Q(x, y)dy=0 (10.5)Линейные уравнения первого порядка
Дифференциальное уравнение 1-го порядка называется линейным, если оно содержит искомую функцию y и ее производнуюв первой степени, т.е. имеет вид: … + P(x)y = Q(x) (10.7) В частном случае P(x) и Q(x) могут быть постоянными числами.Примеры
Уравнения с разделяющимися переменными
№1. Найти общий интеграл уравнения 6ex cos2y dx + (1– 2ex) ctg y dy=0.
Решение. Разделим переменные в данном уравнении, поделив обе его части на выражение cos2y (1–2ex):
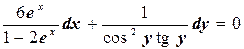 .
.
Интегрируя обе части уравнения, имеем
–3 ln|1–2ex|+ln|tg y| = ln |C|, C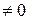
(поскольку C – произвольная постоянная, то для удобства дальнейших преобразований мы заменили С на ln|C|). Отсюда
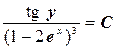 или
или  .
.
Получили общий интеграл данного уравнения. При делении на cos2y(1–2ex) мы могли потерять решения 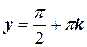 , k – целое число, x= –ln2, но они содержатся в общем интеграле, если подставить значение С = 0.
, k – целое число, x= –ln2, но они содержатся в общем интеграле, если подставить значение С = 0.
№2. Решить уравнение 
Решение. Запишем уравнение в виде  . Разделяя переменные, будем иметь
. Разделяя переменные, будем иметь  и, следовательно,
и, следовательно, 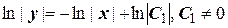 .
.
После потенцирования получим общее решение
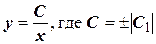 (10.10)
(10.10)
При делении на у мы могли потерять решение у=0, но последнее содержится в формуле (10.10) при С=0.
№3. Найти частное решение ДУ 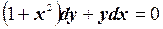 при начальных условиях y(1)=1.
при начальных условиях y(1)=1.
Решение. Разделяя переменные, приведем данное уравнение к виду 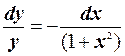 . Интегрируя обе части уравнения, получим
. Интегрируя обе части уравнения, получим  . Это и есть общий интеграл исходного уравнения.
. Это и есть общий интеграл исходного уравнения.
Подставим теперь начальные условия и найдем произвольную постоянную С: 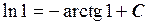 , т.е.
, т.е.  . Следовательно,
. Следовательно,  , откуда получаем искомое частное решение
, откуда получаем искомое частное решение 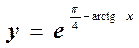 .
.
Однородные уравнения первого порядка
Решение. Данное уравнение является однородным уравнением первой степени… P(λx, λy)=λx+λy=λ(x+y)= λP(x,y), Q(λx, λy)= –λx=λ(–x)=λQ(x,…Линейные уравнения первого порядка
№8. Решить уравнение  .
.
Решение. Здесь P(x)=–ctgx,Q(x)=sinx. Решим уравнение двумя методами.
I. Метод Лагранжа
, , Отсюда . Общее решение ЛНДУ ищем в виде .II. Метод Бернулли
, или .Метод вариации произвольной постоянной
Общее решение ЛОДУ можно записать так х= Су, (так как х=0 – решение). Общее решение заданного (преобразованного) уравнения ищем в виде х=С(у)у… , т.е.Метод подстановки
или . (*) Решим дифференциальное уравнение с разделяющимися переменными ,Варианты заданий
Уравнения с разделяющимися переменными
№10.1. Найти общие интегралы (общие решения) уравнений.
а)  ;
;
б) 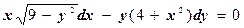 ;
;
в)  ;
;
г)  ;
;
д) 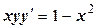 ;
;
е)  ;
;
ж)  ;
;
з) 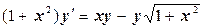 ;
;
и)  ;
;
к)  .
.
№10.2. Найти частные решения уравнений, удовлетворяющие указанным начальным условиям:
а) 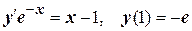 ;
;
б) 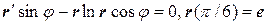 ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  ;
;
ж) 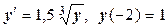 ;
;
з) 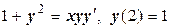 ;
;
и)  ;
;
к) 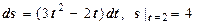 .
.
Однородные уравнения первого порядка
а) ; б) ; в) ;Линейные уравнения первого порядка
а) ; б) ; в) ;Применение дифференциальных уравнений в биологии и медицине.
Скорость размножения некоторых бактерий пропорциональна количеству бактерий в данный момент. Найти зависимость изменения количества бактерий от… Обозначим количество бактерий, имеющихся в данный момент, через х. ТогдаВарианты заданий
1.Скорость укорочения мышцы описывается уравнением
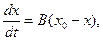
где х0 —полное укорочение мышцы; В — постоянная зависящая от грузки; х — укорочение мышцы в данный момент. Найти закон сокращения мышцы, если в момент времен t=0 величина укорочении мыший была равна 0.
2. Если при прохождении через слой воды толщиной 3 м поглощается половина первоначального количества света, то какая то часть этого количества дойдет до глубины 30 м? Количество света, поглощенного при прохождении через топкий слой воды, пропорционально толщине слоя и количеству света, падающего на его поверхность.
3. Если первоначально количество фермента равно 1 г, а через 1 ч становятся равным 1,2 г, то чему оно будет равно через 5 ч после начала брожения? Скорость прироста фермента считать пропорциональной его наличному количеству.
4. Скорости ферментативных каталитических реакций иногда подсчитываются следующему уравнению:

где х- концентрация продукта в момент времени t: a - начальная концентрация реагента. Найти закон зависимости изменения концентрации продукта от времени.
5. Скорость распада некоторого лекарственного вещества пропорциональна наличному количеству лекарства. Известно, что по истечении 1 ч в организме осталось 31,4 г лекарственного вещества, а по истечении 3 ч – 9,7 г. Определить:
1) сколько лекарственного вещества было введено в организм:
2) через сколько времени после введения в организме останется 1% первоначального количества.
6. За 30 дней распалось 50% первоначального количества радиоактивного вещества. Через сколько времени останется 1% от первоначального количества?
7. Определить период полураспада радия и радона, если постоянные распада данных веществ соответственно равны 1,354·10-11с-1 и 2,1·10-6с-1.
8. Сколько ядер радиоактивного йода 53I131 из каждого миллиарда распадается в 1 с. если период, полураспада 53I131 равен 8 суткам?
9. Счетчик Гейгера, установленный вблизи препарата радиоактивного изотопа серебра, при первом изменении зарегистрировал 5200 (β-частиц в минуту, а через сутки — только 300. Определить период полураспада изотопа.
10. Имеется 1000 относительных единиц радона. Сколько действующих единиц радона останется спустя 1 ч? Постоянная распада радона λ=2,1·10-6с-1
11. Определять, какая доля ядер 80Bi210 распадается за 1 ч, если постоянная распада 80Bi210 λ= 1,61·10-6с-1
Контрольные вопросы
1. Дайте определение дифференциального уравнения. Математическая запись ДУ. Примеры представления ДУ.
2. Что такое порядок ДУ? Приведите примеры записи ДУ различных порядков.
3. Дайте определение решения (интеграла) ДУ, общего решения, частного решения, начальных условий.
4. В чем состоит задача Коши?
5. В чем заключается интегрирование ДУ?
6. Что такое интегральная кривая? Чем отличаются графически общее решение ДУ и частное решение ДУ?
7. Дайте определение и приведите примеры ДУ с разделяющимися переменными.
8. Что такое однородная функция степени n?
9. Дайте определение и приведите примеры однородного ДУ.
10. Дайте определение линейного ДУ 1-го порядка.
11. Перечислите и объясните суть методов решений ЛНДУ 1-го порядка.
12. Приведите примеры применения дифференциальных уравнений в биологии и медицине.
Глава 11. Численные методы решения дифференциальных уравнений
Известные методы точного интегрирования дифференциальных уравнений позволяют найти решение в виде аналитической функции, однако эти методы применимы для очень ограниченного класса уравнений. Большинство уравнений, встречающихся при решении практических задач нельзя проинтегрировать с помощью этих методов.
В таких случаях используются численные методы решения, которые представляют решение дифференциального уравнения не в виде аналитической функции, а в виде таблиц значений искомой функции в зависимости от значения переменной.
Существует несколько методов численного интегрирования дифференциальных уравнений, которые отличаются друг от друга по сложности вычислений и точности результата.
Рассмотрим некоторые из них.
Метод Эйлера
Известно, что уравнение задает в некоторой области поле направлений. Решение этого уравнения с некоторыми начальными условиями дает кривую, которая… Если взять последовательность точек х0, х1, х2, …. и заменить на получившихся… При подстановке заданных начальных условий (х0, у0) в дифференциальное уравнение получаем угловой коэффициент…Примеры
№1. Решить методом Рунге – Кутта дифференциальное уравнение  при начальном условии у(0) = 1 на отрезке [0; 0,5] с шагом 0,1.
при начальном условии у(0) = 1 на отрезке [0; 0,5] с шагом 0,1.
Решение.
Для i = 0 вычислим коэффициенты ki:
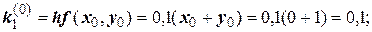
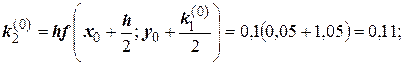
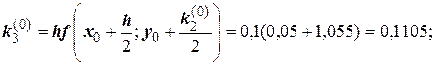


Последующие вычисления приводить не будем, а результаты представим в виде таблицы.
| i | xi | k | Dyi | yi | |
| 0,1000 | 0,1104 | ||||
| 0,1100 | |||||
| 0,1105 | |||||
| 0,1211 | |||||
| 0,1 | 0,1210 | 0,1325 | 1,1104 | ||
| 0,1321 | |||||
| 0,1326 | |||||
| 0,1443 | |||||
| 0,2 | 0,1443 | 0,1569 | 1,2429 | ||
| 0,1565 | |||||
| 0,1571 | |||||
| 0,1700 | |||||
| 0,3 | 0,1700 | 0,1840 | 1,3998 | ||
| 0,1835 | |||||
| 0,1842 | |||||
| 0,1984 | |||||
| 0,4 | 0,1984 | 0,2138 | 1,5838 | ||
| 0,2133 | |||||
| 0,2140 | |||||
| 0,2298 | |||||
| 0,5 | 1,7976 |
№2. Решим предыдущий пример методом Эйлера.
Решение.
Применяем формулу 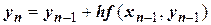


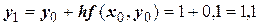


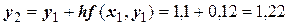
Производя аналогичные вычисления далее, получаем таблицу значений:
| i | ||||||
| xi | 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| yi | 1,1 | 1,22 | 1,362 | 1,528 | 1,721 |
Применим теперь уточненный метод Эйлера (точность 0,001).
| i | ||||||
| xi | 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| yi | 1,111 | 1,243 | 1,400 | 1,585 | 1,799 |
Для сравнения точности приведенных методов численного решение данного уравнения решим его аналитически и найдем точные значения функции у на заданном отрезке.
Уравнение  является линейным неоднородным дифференциальным уравнением первого порядка. Решим соответствующее ему однородное уравнение.
является линейным неоднородным дифференциальным уравнением первого порядка. Решим соответствующее ему однородное уравнение.
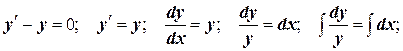
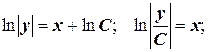
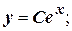
Решение неоднородного уравнения имеет вид 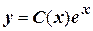 .
.

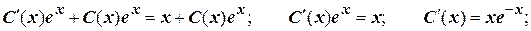
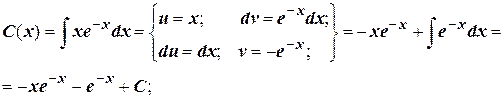
Общее решение: 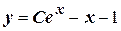 .
.
C учетом начального условия: 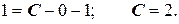
Частное решение:  .
.
Для сравнения полученных результатов составим таблицу.
| i | xi | yi | |||
| Метод Эйлера | Уточнен-ный метод Эйлера | Метод Рунге-Кутта | Точное значение | ||
| 0,1 | 1,1 | 1,111 | 1,1104 | 1,1103 | |
| 0,2 | 1,22 | 1,243 | 1,2429 | 1,2428 | |
| 0,3 | 1,362 | 1,4 | 1,3998 | 1,3997 | |
| 0,4 | 1,528 | 1,585 | 1,5838 | 1,5837 | |
| 0,5 | 1,721 | 1,799 | 1,7976 | 1,7975 |
Как видно из полученных результатов метод Рунге – Кутта дает наиболее точный ответ. Точность достигает 0,0001. Кроме того, следует обратить внимание на то, ошибка (расхождение между точным и приближенным значениями) увеличивается с каждым шагом вычислений. Это обусловлено тем что, во-первых, полученное приближенное значение округляется на каждом шаге, а во-вторых – тем что, в качестве основы вычисления принимается значение, полученное на предыдущем шаге, т.е. приближенное значение. Таким образом, происходит накопление ошибки.
Это хорошо видно из таблицы. С каждым новым шагом приближенное значение все более отличается от точного.
Варианты заданий
№11.1. Решить с помощью методов Эйлера, уточненного метода Эйлера, Рунге-Кутта и аналитически следующие дифференциальные уравнения при заданных начальных условиях, на заданном отрезке с шагом 0,2. Сравнить полученные результаты.
| № варианта | Уравнение

| Начальные условия (x0, y0) | Отрезок [x0,xк] |

| x0= –1,y0= 0 | [–1, 1] | |

| x0= 0, y0= 2 | [0, 2] | |

| x0= 1, y0= 0 | [1, 3] | |

| x0= 0, y0= 2 | [0, 2] | |

| x0= 0, y0= 2 | [0, 2] | |

| x0= 1, y0= 1 | [1, 3] | |
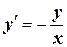
| x0= 1, y0= 1 | [1, 3] | |
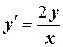
| x0= 1,y0= 2 | [1, 3] | |

| x0= 0, y0= 2 | [0, 2] | |
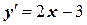
| x0= 2, y0= 0 | [2, 4] | |

| x0= 0, y0= 3 | [0, 2] | |
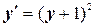
| x0= –3, y0= –2 | [–3, –1] | |

| x0= –2, y0= 1 | [–2, 0] | |
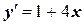
| x0= –3, y0= 5 | [–3, –1] | |
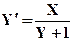
| X0= - 4,Y0= 4 | [-4,-2] | |

| X0= 2,Y0= 2 | [2,- 4] | |
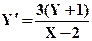
| X0= 3,Y0= 0 | [3,5] | |
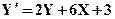
| X0= 0,Y0= -2 | [0,2] | |

| X0= -3,Y0= 1 | [-3,-1] | |
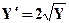
| X0= 2,Y0= 9 | [2,4] | |

| X0= -2,Y0= -0.4 | [-2,0] | |

| X0= - 4,Y0= -2 | [-4,-2] | |

| X0= 0,Y0= 2 | [0,2] | |
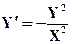
| X0= 1,Y0= 1 | [1,3] |
Контрольные вопросы
1. Когда применяются численные методы решения дифференциальных уравнений?
2. Перечислите известные вам численные методы решения дифференциальных уравнений.
3. В чем заключается суть метода Эйлера?
4. В чем смысл уточненного метода Эйлера?
5. В чем смысл метода Рунге-Кутта?
6. Как рассчитать погрешность вычислений в приближенных методах?
Глава 12. Элементы теории вероятностей
Случайное событие
Теория вероятностей – математическая наука, изучающая закономерности случайных явлений. Теория вероятности изучает случайные события и случайные величины. Случайное событие – это любой факт, который в результате испытания может произойти или не произойти. Случайное событие…Комбинаторика
Комбинаторика — раздел математики, изучающий вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).… Размещениями из n различных элементов по m элементов (m ≤ n) называются… Например, из трех элементов a, b, c можно составить по два элемента следующие размещения: ab, ас, bc, ba, ca, cb.Вероятность случайного события
Численная мера степени объективности возможности наступления события называется вероятностью случайного события. Классическое определение вероятности события А:Закон сложения вероятностей
Сумма двух событий – это такое событие, при котором появляется хотя бы одно из этих событий (А или В). Если А и В совместные события, то их сумма А + В обозначает наступление… Если А и В несовместные события, то сумма А + В означает наступление или события А или события В.Варианты заданий
№12.1. В коробке 30 таблеток: 10 красных, 5 желтых, 15 белых. Найти вероятность появления цветной таблетки (т.е. или красной или желтой).
№12.2. В картотеке имеются истории болезней 8 пациентов. Если наугад взять первую, затем вторую, третью и т.д. истории болезней, то какова вероятность в каждом случае изъятия нужной истории болезни? Предполагается, что искомая история болезни имеется в картотеке. Рассмотрите 2 варианта: а) взятые истории болезней не возвращаются в картотеку; б) взятые истории болезней каждый раз возвращаются в картотеку и хаотически располагаются в ней.
№12.3. В коробке имеется 7 желтых и несколько белых таблеток. Какова вероятность вытащить белую таблетку, если вероятность вытащить желтую таблетку равна 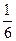 .Сколько белых таблеток в коробке?
.Сколько белых таблеток в коробке?
№12.4. Наудачу выбрано натуральное число, не превосходящее 10. Какова вероятность того, что это число является простым?
№12.5. Набирая номер телефона, абонент забыл одну цифру, и набрал ее наугад. Какова вероятность того, что набранная цифра правильная?
№12.6. Одна секретарша напечатала 5 различных писем и надписала 5 конвертов с адресами. Предположим, что она вкладывает письма в конверты случайным образом. Какова вероятность того, что ровно четыре письма будут вложены в конверты с адресами тех лиц, кому они предназначены?
№12.7. Числа от 1 до 100 записывают на полосках бумаги, которые помещают в чашу. После продолжительного встряхивания случайным образом извлекают одну полоску.
а) Какова вероятность того, что появится число, делящееся на 3?
б) Какова вероятность того, что появится число, делящееся на 3 и на 5?
№12.8. Профессор выставляет 20 разных оценок за контрольные работы 20 студентов группы и заносит их в компьютер. При распечатке ведомости из-за ошибки в компьютере оценки случайно смешались.
а) Какова вероятность того, что каждый студент получит свою верную оценку?
б) Какова вероятность того, что ровно 19 студентов получат свои верные оценки?
№12.9. В клетке содержат 6 белых и 4 серых мыши. Рассмотрим эксперимент, состоящий в случайном извлечении из клетки трех мышей.
а) Опишите пространство выборок этого эксперимента.
б) Вычислите вероятность для четырех возможных комбинаций цвета мышей (3 белых, 2 белых и 1 серая и т.д.).
№12.10. Из 20 человек, одновременно заболевших гриппом, 15 выздоровели полностью за три дня. Предположим, что из этих 20 человек случайным образом выбиралось 5. Какова вероятность того, что все 5 выздоравливают за три дня? что выздоравливают только 4 человека? что ни один не выздоравливает?
№12.11. Требуется выбрать наудачу 10 человек из группы в 10 мужчин и 10 женщин.
а) Какова вероятность того, что выбрано 10 мужчин?
б) Какова вероятность того, что выбрано больше мужчин, чем женщин?
в) Какова вероятность того, что выбрано по крайней мере 8 мужчин?
№12.12. За игрушечной пишущей машинкой с буквами A, В, С, D и Е сидит шимпанзе. Если шимпанзе печатает четыре случайных буквы, то:
а) какова вероятность того, что окажется напечатанным слово «BEAD» («шарик»)?
б) какова вероятность того, что все напечатанные буквы одинаковы?
№12.13. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.
№12.14. В сосуд емкостью 10 л попала ровно одна болезнетворная бактерия. Какова вероятность зачерпнуть ее при наборе из этого сосуда стакана воды (200 см3)?
№12.15. Вероятность того, что некий человек умрет на 71-м году жизни, равна 0,04. Какова вероятность того, что человек не умрет на 71-м году?
№12.16. При изучении миграций белого медведя девять медведей были помечены числами от 1 до 9. Три медведя отловлены повторно.
а) Пусть Аi обозначает событие, состоящее в том, что i-й отловленный медведь помечен четным числом. Какова вероятность Р(A1), Р(А2), Р(А3)?
б) Найдите события A1+A2 и A1+А2+А3.
№12.17. В ванну, где содержатся 3 рыбы: А, В и С, время от времени помещают кусочки пищи. Каждый раз, когда бросают кусочек, рыбы конкурируют за него. Допустим, что за длительный период было установлено, что А или В добивались успеха в течение 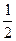 времени, а А или С в течение
времени, а А или С в течение 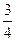 всего времени наблюдения. 1) Какова вероятность того, что добивается успеха рыба A? 2) Какая из рыб накормлена лучше
всего времени наблюдения. 1) Какова вероятность того, что добивается успеха рыба A? 2) Какая из рыб накормлена лучше
№12.18. В некоторую больницу поступают пациенты с четырьмя видами болезней. Многолетние наблюдения показали, что этим группам соответствуют относительные частоты 0,1; 0,4; 0,3; 0,2. Для лечения заболеваний с частотой 0,1 и 0,2 необходимо переливание крови. Какое количество больных следует обеспечить кровью, если в течение месяца поступило 1000 больных
№12.19. Опухоль-"мишень" разделена на три области. При использовании радионуклидного препарата вероятность поражения первой области равна 0,45; второй - 0,35. Найти вероятность того, что при однократном использовании радионуклид попадет либо в первую, либо во вторую область.
№12.20. Брошена игральная кость. Найти вероятность того, что выпадет четное или кратное трем число очков.
№12.21. Консультационный пункт университета получает пакеты с контрольными работами из городов A, В и С. Вероятность получения пакета из города A равна 0,6, а из города В - 0,1. Найти вероятность того, что очередной пакет будет получен из города С.
№12.22. С первого предприятия поступило 200 пробирок, из которых 190 стандартных, а со второго - 300, из которых 280 стандартных. Найти вероятность того, что наудачу взятая пробирка будет стандартной.
№12.23. На тридцати историях болезни написаны 30 двузначных чисел от 1 до 30 (их порядковые номера). Эти истории болезни лежат на полке в случайном порядке. Какова вероятность вынуть историю болезни с номером кратным 2 или 3?
№12.24. В некоторой популяции у 40% людей волосы темные, у 40% — рыжие и у 20% —светлые. В этой популяции у всех темноволосых людей глаза карие, у всех светловолосых — голубые, у одной половины рыжеволосых — голубые, а у другой — карие. Пусть А1, А2 и А3 — события, состоящие в том, что у человека соответственно темные, рыжие и светлые волосы, и пусть B1 и В2 соответственно обозначают карие и голубые глаза.
а) Найдите Р(А1), Р(B1), Р(В2) и Р(А1+B2).
б) Опишите событие А1+A2+A3. Найдите вероятность этого события.
№12.25. В популяции из 2000 плодовых мушек у 250 особей обнаруживают рецессивный признак крыла W и у 150 - рецессивный признак глаза Е. Предположим, что у 50 мушек обнаруживают оба признака. Для эксперимента по скрещиванию из популяции выбирают одну мушку.
а) Какова вероятность, что у этой мушки будет признак W? E?
б) Какова вероятность, что присутствует признак W и E?
в) Вычислите Р( ).
).
Условная вероятность, закон умножения вероятностей
Условная вероятность события В – это вероятность события В, найденная при условии, что событие А произошло. Обозначается Р(В|А). В коробке содержится 3 белых и 3 желтых таблетки. Из коробки дважды вынимают наугад по одной таблетке, не возвращая их…Варианты заданий
№ 12.1. В одном аквариуме находятся: 3 белые, 3 красные и 3 голубые рыбки. Трех случайно выбранных рыбок переносят в другой аквариум. Какова вероятность того, что все 3 рыбки белые?
№ 12.2. Студент изучает биологию, химию и физику. Он оценивает, что вероятность получить "пятерку" по этим предметам равна соответственно: Р(Б) = 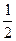 ; Р(X) =
; Р(X) = 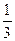 ; Р(Ф) =
; Р(Ф) =  . Предположим, что оценки студента по трем предметам независимы. Какова вероятность, что он: 1) Не получит ни одной "пятерки"? 2) Получит "пятерку" только по биологии?
. Предположим, что оценки студента по трем предметам независимы. Какова вероятность, что он: 1) Не получит ни одной "пятерки"? 2) Получит "пятерку" только по биологии?
№ 12.3. На стеллаже библиотеки в случайном порядке - 7 учебников по химии, из которых три - в переплете. Было вытащено наудачу 2 учебника. Какова вероятность, что оба учебника будут в переплете?
№ 12.4. На лекции по биофизике во втором семестре присутствуют 124 студента. Из них на экзамене по высшей математике в зимнюю сессию получили оценку "отлично" 19 человек, "хорошо" – 50 человек, "удовлетворительно" – 24 и не сдали экзамен 31 человек. Какова вероятность того, что вызванные наугад один за другим два студента из числа присутствующих на лекции не имеют задолженности по высшей математике?
№ 12.5. Студент пришел на зачет, зная из 30 вопросов только 24. Какова вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель задает еще один вопрос?
№ 12.6. Вероятность того, что в течение одного рабочего дня возникнет неполадка в определенном медицинском приборе равна 0,05. Какова вероятность того, что не произойдет ни одной неполадки за 3 рабочих дня?
№ 12.7. Вероятность того, что в летнюю сессию студент сдаст первый экзамен, равна 0,8; второй - 0,9; третий - 0,8. Какова вероятность того, что он сдаст только первый экзамен?
№ 12.8. В коробке содержится 3 белых и 3 желтых таблетки. Из коробки дважды вынимают наудачу по одной таблетке, не возвращая в коробку. Найти вероятность появления белой таблетки при втором испытании (событие В), если при первом испытании была извлечена желтая таблетка (событие A).
№ 12.9. В коробке содержится 8 красных и 6 белых таблеток. Из коробки последовательно без возвращения извлекаются 3 таблетки. Найти вероятность того, что все таблетки белые.
№ 12.10. Предположим, что в некоторой семье имеются 2 ребенка. 1) Какова вероятность того, что оба ребенка - девочки? 2) Если известно, что, по крайней мере, один ребенок --девочка, то какова вероятность того, что оба ребенка - девочки? 3) Если известно, что старший ребенок -девочка, то какова вероятность, что оба ребенка - девочки?
№ 12.11. Вероятность того, что в летнюю сессию студент сдаст первый экзамен, равна 0,8; второй - 0,9; третий - 0,8.Найти вероятность того, что студент сдаст хотя бы один экзамен.
№ 12.12. Отдел технического контроля проверяет медицинское изделие на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное.
№ 12.13. Какова вероятность того, что у девочки, о которой известно, что она растет в семье, где четыре ребенка, есть старший брат?
№ 12.14. а) Сколько должна планировать супружеская пара иметь детей, чтобы вероятность хотя бы одного мальчика была выше 90%?
б) Сколько должна планировать супружеская пара иметь детей, чтобы вероятность хотя бы одного мальчика и одной девочки была выше 70%?
№ 12.15. а) Найдите вероятность того, что в семье из шестерых детей три мальчика и три девочки.
б) Найдите вероятность того, что в семье из шестерых детей все дети одного и того же пола.
№ 12.16. Представим, что в одной семье есть восемь детей — четыре мальчика и четыре девочки. Какова вероятность того, что старший ребенок – мальчик? Какова вероятность того, что все четыре мальчика старше четырех девочек?
№ 12.17. У пары три ребенка. Определим события А (первый ребенок – девочка), В (второй ребенок – мальчик), С (третий ребенок – мальчик), D (первые два ребенка – мальчики) и Е (хотя бы один ребенок –мальчик).
а) Вычислите вероятности этих пяти событий.
б) Являются ли независимыми А и D; А и Е; В и E?
в) Являются ли независимыми события В, С и E?
№ 12.18. Некоторая вакцина эффективна на 75% в формировании иммунитета. Вакцинировалось два человека. Пусть А и В — события, состоящие в том, что соответственно первый и второй человек приобретает иммунитет. Являются ли независимыми А и В; А и 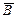 ;
; 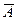 и В;
и В; 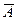 и
и 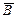 ? Найти вероятности этих пар событий.
? Найти вероятности этих пар событий.
№ 12.19. Три врача независимо друг от друга осмотрели одного и того же больного. Вероятность того, что 1-ый врач допустит ошибку при установлении диагноза, равна 0,01. Для 2-го и 3-го – 0,015 0,02 соответственно. Найти вероятность того, что хотя бы один из врачей допустит ошибку в диагнозе.
№ 12.20. Три крысы обучаются выполнению трех различных заданий (по одной крысе на каждое задание). Вероятности того, что крысы выполняют свои задания за 1 мин, составляют соответственно 2/3, 1/2 и 1/3. Какова вероятность того, что все три крысы выполнят свои задания за 1 мин? Что выполнят только две? Что выполнят хотя бы две?
№ 12.21. В одном городе вероятность грозы в любой данный день в течение августа составляет 0,25, а вероятность града — 0,1. Вероятность града во время грозы равна 0,3.
а) Являются ли независимыми события «град» и «гроза»?
б) Какова вероятность града в такой день, когда нет грозы?
№ 12.22. На трех фермах A, В и С произошла вспышка заболевания ящуром. Доля зараженного скота составляют соответственно 1/6, 1/4 и 1/3. Из каждой фермы случайным образом выбирают по одной корове.
а) Какова вероятность того, что заболевание имеется только у одной коровы?
б) Если заражена только одна корова, то какова вероятность, что эта корова выбрана из фермы A?
№ 12.23. Медицинский прибор проходит 3 стадии обработки. Вероятность получения брака на первой стадии равна 0,02; на второй – 0,03; на третьей – 0,02. Найдите вероятность получения прибора без брака после 3 стадий, предполагая, что получения брака на отдельных стадиях являются независимыми событиями.
№ 12.24. Студент успел подготовить к экзаменам 20 вопросов из 25. Какова вероятность того, что из 3 наудачу выбранных вопросов студент знает не менее 2?
№ 12.25. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором и третьем справочниках, равна соответственно 0,6, 0,7 и 0,8. Найти вероятность того, что эта формула содержится не менее чем в двух справочниках.
Формулы полной вероятности и Байеса
Вероятность события A, которое может наступить лишь при условии появления одного из n попарно несовместимых событий B1, B2, ..., Bn, образующих… (формула полной вероятности).Формулы Бернулли, Пуассона и Муавра-Лапласа
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие… Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом…Варианты заданий
№12.1. Вероятность успеха в эксперименте составляет 95%, а неудачи—-5%. Эксперимент повторяют пять раз. Определите вероятности следующих событий а) ни одного успеха: б) ни одной неудачи; в) четыре успеха и одна неудача.
№12.2. В любой данный день в июне погода может быть хорошей (с вероятностью 50%), посредственной (с вероятностью 25%) или плохой (с вероятностью 25%). Предположим, что погода в данный день никак не влияет на погоду в любой другой день. Какова вероятность того, что в течение одной недели в июне будет семь хороших дней? четыре хороших дня, два посредственных и один плохой день?
№12.3. В некоторой большой популяций у 40% людей волосы черные, у 40% рыжие и у 20% светлые. Если из популяции случайно выбирают 10 человек, то каковы вероятности следующих событий:
а) 5 черноволосых, 5 рыжих;
б) 4 черноволосых, 4 рыжих, 2 светловолосых;
в) 3 черноволосых, 3 рыжих, 4 светловолосых?
№12.4. Дальтонизмом страдает 1% большой популяции. Допустим, что из нее наугад выбирают n человек. Какова вероятность того, что ни один из n человек не окажется дальтоником? Сколь велико должно быть n, чтобы эта вероятность была меньше 10%?
№12.5. Машина дает продукцию, которая должна удовлетворять определенным требованиям. Вероятность того, что данная единица продукции приемлема, составляет 95%. Из продукции машины делают выборку в количестве 10 ед. Какова вероятность того, что все 10 ед. продукции окажутся приемлемыми?
№12.6. По оценкам, волк, в одиночку нападающий на лося, добивается успеха в 8% столкновений. Какова вероятность того, что в пяти столкновениях ни один лось не станет добычей волка?
№12.7. В каждом полушарии человеческого мозга имеется четко определяемая слуховая область. В анатомических исследованиях было установлено, что слуховая область левого полушария более развита в 65% рассмотренных случаев, менее развита в 10% и развита в одинаковой с правым полушарием степени в 25% случаев. Какова вероятность того, что из группы в пять случайно выбранных человек в три эти категории соответственно попадут три, ни одного и два человека?
№12.8. Замечено, что слушатели вводного курса по количественному химическому анализу достигают приемлемых результатов в 80% титрований. Один студент добился приемлемого результата лишь однажды в шести титрованиях. Какова вероятность случайного наступления этого события? Как вы думаете, станет ли этот студент химиком-экспериментатором?
№12.9. При заболеваниях щитовидной железы применяется йодная терапия. Было замечено, что у 50% больных наступает быстрое улучшение, на 40% больных терапия не оказывает заметного эффекта, а у 10% она вызывала ухудшение состояния. Эту терапию применяют девять больных. Каковы вероятности того, что: а) все девять почувствуют улучшение; б) у пятерых будет улучшение, трое останутся в прежнем состоянии и одному станет хуже; в) у троих будет, улучшение, трое останутся в прежнем состоянии и троим станет хуже?
№12.10. Лечение одного заболевания приводит к выздоровлению в 75% случаев. Лечилось шесть больных. Каковы вероятности того, что: а) выздоровят все шестеро; б) не выздоровит ни один; в) выздоровят по крайней мере четверо?
№12.11. Шесть человек больны заболеванием, для которого коэффициент выздоровления составляет 98%. Каковы вероятности того, что: а) выздоровят все шестеро; б) ни один не выздоровит; б) выздоровят только пятеро?
№12.12. Шансы волка добыть пищу за каждый период охоты составляют 60%. Какова вероятность того, что успешными оказалось больше половины всех периодов охоты, если всего был 31 период? если всего было 14 периодов?
№12.13. а) Сколько нужно бросить костей, чтобы вероятность выпадения нечетного числа хотя бы на одной из них была больше 90%? б) Сколько нужно бросить костей, чтобы вероятность выпадения хотя бы одной пятерки была больше 50%?
№12.14. В одном городе 50% населения предпочли бы более строгий контроль за огнестрельным оружием, 30% — более слабый контроль и 20% хотели бы сохранить существующее положение вещей. Для опроса выбрано случайным образом 12 человек. Каковы вероятности того, что: а) все хотят усилить контроль; б) половина опрошенных хотят усилить, а половина — ослабить контроль; в) равные количества опрошенных предпочитают три альтернативы?
№12.15. Метеоролог обращается за субсидией для поездки в Испанию с целью проверки теории о том, что «дождь в Испании идет в основном на равнине». Он планирует провести наблюдения в такое время года, когда вероятность дождя на равнине в любой данный день составляет 20%. (Предполагается, что эта, вероятность не зависит от предшествующей погоды.)
а) Сколько дней должен запланировать метеоролог провести в Испании, чтобы на 99% быть уверенным в том, что он застанет дождь?
б) Допустим, что метеорологу были выделены денежные средства на 15 дней в Испании и что за первые 10 дней не было ни одного дождя. Какова вероятность того, что его поездка окажется неудачной, т. е. что он не увидит ни одного дождя?
№12.16. В популяции дрозофилы у 20% особей имеется мутация крыльев. Если из популяции выбирают наугад шесть мух, то какова вероятность мутации у двух из них? по крайней мере у одной? меньше чем у пяти?
№12.17. Кофеин и бензедрин считаются стимуляторами, имеющими некоторую способность противодействовать угнетающему влиянию алкоголя. В эксперименте по проверке их относительной эффективности 40 добровольцев приняли по 6 унций алкоголя каждый. Добровольцы были разбиты затем на 20 пар, и один член каждой пары получал бензедрин, а другой — кофеин. Согласно некоторому тесту, бензедрин приводил к более быстрому восстановлению во всех 20 парах. Какова вероятность такого результата, если считать, что в воздействии кофеина и бензедрина нет никакой разницы?
№12.18. В хлопке имеется 10% коротких волокон. Какова вероятность того, что в наудачу взятом пучке из пяти волокон окажется не более двух коротких?
№12.19. Всхожесть семян данного растения оценивается вероятностью 0,8. Найти вероятность того, что из 8 посеянных семян взойдёт не менее 6.
№12.20. Найти наивероятнейшее число появлений некоторого события при 16 испытаниях, если вероятность появления его в отдельном испытании равна 0,7.
№12.21. Число длинных волокон в партии хлопка составляет в среднем 0,6 общего количества волокон. При каком общем количестве волокон хлопка наивероятнейшее число длинных окажется равным 20?
№12.22. На каждые 20 приборов приходится в среднем 6 неточных. Определить наивероятнейшее число точных приборов из наудачу взятых 8 приборов.
№12.23. Если в среднем левши составляют 1 %, то какова вероятность того, что среди 200 человек: 1) 4 левши; 2) по крайней мере 4 левши.
№12.24. В аптеку поступило 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Определить вероятность того, что аптека получит разбитых бутылок:
1) ровно одну; 2) хотя бы одну.
№12.25. Дежурная аптека обслуживает 20000 населения. Вероятность того, что в ночное время один посетитель придет в аптеку, равна 0,0002. Найти вероятность того, что в ночное время в аптеку:
а) никто не придет;
б) придут 3 посетителя;
в) придет хотя бы один посетитель.
Случайные величины
Дискретная случайная величина - это случайная величина, когда принимает отдельное изолированное, счетное множество значений. Непрерывная случайная величина - это случайная величина, принимающая любые… Случайные величины обозначаются конечными заглавными буквами латинского алфавита X, Y, Z, а их значения -…Закон распределения случайной величины
Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически. Таблица - это простейшая форма задания закона распределения. В ней перечислены…Функция распределения случайных величин
F(x) = Р(Х < х). Ее также называют интегральной функцией распределения дискретных и непрерывных случайных величин. Свойства функции распределения: 0≤F(x)≤1Числовые характеристики дискретной случайной величины
. Свойства математического ожидания: M(C)=C, где C – произвольная постояннаяПлотность вероятности непрерывных случайных величин
f(x) = F' (x). Ее также называют дифференциальной функцией распределения. График плотности распределения f(x) называется кривой распределения.Нормальный закон распределения
Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами µ и σ2, если ее плотность вероятности имеет… (см. рис. 12.5а). Свойства плотности распределения вероятностей:Варианты заданий
№12.1. Случайная величина X задана законом распределения:

| |||

| 0,1 | 0,4 | 0,5 |
Найти математическое ожидание и среднее квадратическое отклонение. Построить многоугольник распределения.
№12.2. Найти дисперсию случайной величины X, зная закон ее распределения. Построить многоугольник распределения.

| -1 | |||

| 0,48 | 0,01 | 0,09 | 0,42 |
№12.3. Дискретная случайная величина X имеет закон распределения.

| 0,2 | 0,4 | 0,6 | 0,8 | |

| 0,1 | 0,2 | 0,4 | P4 | 0,1 |
Чему равна вероятность Р4(X=0,8)? Построить многоугольник распределения. Найти математическое ожидание и дисперсию.
№12.4. Дискретная случайная величина X имеет закон распределения.

| |||||

| P1 | 0,15 | P3 | 0,25 | 0,35 |
Найти вероятность Р1(х = 3) и P3(х = 5), если известно, что Р3 в 4 раза больше Р1. Построить многоугольник распределения. Найти математическое ожидание и дисперсию.
№12.5. Дискретная случайная величина x– число мальчиков в семьях с 3 детьми. Предполагая равновероятными рождения мальчика и девочки: а) составьте ряд распределения числа рождений мальчиков; б) постройте многоугольник распределения.
№12.6. 2 стрелка стреляют по одной мишени, делая независимо друг от друга по 2 выстрела. Вероятность попадания в мишень для первого стрелка равна 0,5, для второго – 0,6. Найдите закон распределения случайной величины x, равной общему числу попаданий в мишень.
№12.7. Дискретная случайная величина x задана таблицей распределения:
| xi | -1 | ||
| pi | 0,25 | 0,5 | 0,25 |
Найдите функцию распределения F(x) и, используя ее, найдите вероятность события 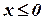 . Постройте график функции F(x).
. Постройте график функции F(x).
№12.8. Случайная величина X имеет плотность вероятности

Найдите функцию распределения F(x)и вероятность события 
№12.9. Плотность вероятности случайной величины x, распределенной равномерно на отрезке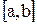 , имеет вид:
, имеет вид:

Найдите математическое ожидание величины x.
№12.10. Даны все возможные значения дискретной случайной величины X: x1=1, x2=2, x3=3, а также известны  Найдите закон распределения величины x.
Найдите закон распределения величины x.
№12.11. Найдите математическое ожидание и среднее квадратическое отклонение случайной величины x, имеющей плотность вероятности
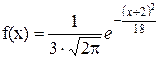 .
.
Пользуясь правилом «трех сигм», укажите интервал, симметричный относительно математического ожидания, в который попадает случайная величина xс вероятностью 0,9973.
Глава 13. Статистический анализ результатов исследований
Основные понятия математической статистики
Математическая статистика – это раздел математики, изучающий приближенные методы сбора и анализа данных по результатам эксперимента для выявления существующих закономерностей, т.е. отыскания законов распределения случайных величин и их числовых характеристик.
В математической статистике принято выделять два основных направления исследований:
1.Оценка параметров генеральной совокупности.
2.Проверка статистических гипотез (некоторых априорных предположений).
Основными понятиями математической статистики являются: генеральная совокупность, выборка, теоретическая функция распределения.
Генеральной совокупностью является набор всех мыслимых статистических данных при наблюдениях случайной величины.
ХГ = {х1, х2, х3, …, хN, } = { хi ; i=1,N }
Наблюдаемая случайная величина Х называется признаком или фактором выборки. Генеральная совокупность – есть статистический аналог случайной величины, ее объем N обычно велик, поэтому из нее выбирается часть данных, называемая выборочной совокупностью или просто выборкой.
ХВ = {х1, х2, х3, …, хn, } = { хi ; i=1,n }
ХВ Ì ХГ, n £ N
Выборка – это совокупность случайно отобранных наблюдений (объектов) из генеральной совокупности для непосредственного изучения. Количество объектов в выборке называется объемом выборки и обозначается n. Обычно выборка составляет 5%-10% от генеральной совокупности.
Использование выборки для построения закономерностей, которым подчинена наблюдаемая случайная величина, позволяет избежать ее сплошного (массового) наблюдения, что часто бывает ресурсоемким процессом, а то и просто невозможным.
Например, популяция представляет собой множество индивидуумов. Изучение целой популяции трудоемко и дорого, поэтому собирают данные по выборке индивидуумов, которых считают представителями этой популяции, позволяющими сделать вывод относительно этой популяции.
Однако, выборка обязательно должна удовлетворять условию репрезентативности, т.е. давать обоснованное представление о генеральной совокупности. Как сформировать репрезентативную (представительную) выборку? В идеале стремятся получить случайную (рандомизированную) выборку. Для этого составляют список всех индивидуумов в популяции и случайно их отбирают. Но иной раз затраты при составлении списка могут оказаться недопустимыми и тогда берут приемлемую выборку, например, одну клинику, больницу и исследуют всех пациентов в этой клинике с данным заболеванием.
Каждый элемент выборки  называется вариантой. Число повторений варианты
называется вариантой. Число повторений варианты 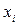 в выборке называется частотой встречаемости
в выборке называется частотой встречаемости  . Величина
. Величина  называется относительной частотой варианты, т.е. находится как отношение абсолютной частоты варианты
называется относительной частотой варианты, т.е. находится как отношение абсолютной частоты варианты  ко всему объему выборки. Последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом.
ко всему объему выборки. Последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом.
Рассмотрим три формы вариационного ряда: ранжированный, дискретный и интервальный.
Ранжированный ряд - это перечень отдельных единиц совокупности в порядке возрастания изучаемого признака.
Дискретный вариационный ряд представляет собой таблицу, состоящую из граф, либо строк: конкретного значения признака хi и абсолютной частоты ni (или относительной частоты ωi) проявления i-го значения признака x.
Примером вариационного ряда служит таблица
| Значение | 
| 14,3 | 14,7 | 15,0 | 15,5 | |
| Частота | 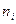
| 0,08 | 0,16 | 0,29 | 0,34 | 0,13 |
Статистическое распределение – это совокупность вариант  и соответствующих им частот
и соответствующих им частот 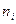 . Для проверки правильности записи статистического распределения используют условие нормировки:
. Для проверки правильности записи статистического распределения используют условие нормировки:  .
.
Задано распределение частот выборки объема n=20.

| |||
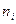
|
Написать распределение относительных частот.
Решение: Найдем относительные частоты. Для этого разделим частоты на объем выборки:

Распределение относительных частот имеет вид:

| |||
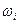
| 0,15 | 0,5 | 0,35 |
Контроль: 0,15 + 0,5 + 0,35 = 1.
Дискретный ряд можно изобразить графически. В прямоугольной декартовой системе координат отмечаются точки с координатами ( ) или (
) или (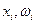 ), которые соединяются прямыми линиями. Такую ломаную называют полигоном частот.
), которые соединяются прямыми линиями. Такую ломаную называют полигоном частот.
Построить дискретный вариационный ряд (ДВР) и начертить полигон распределения 45 абитуриентов по числу баллов, полученных ими на приемных экзаменах:
39 41 40 42 41 40 42 44 40 43 42 41 43 39 42 41 42 39 41 37 43 41 38 43 42 41 40 41 38 44 40 39 41 40 42 40 41 42 40 43 38 39 41 41 42.
Решение: Для построения вариационного ряда различные значения признака x (варианты) располагаем в порядке их возрастания и под каждым из этих значений записываем его частоту.

| ||||||||
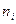
|
Построим полигон этого распределения:

Рис. 13.1. Полигон частот
Интервальный вариационный ряд используется при большом числе наблюдений. Для построения такого ряда надо выбрать число интервалов признака и установить длину интервала. При большом числе групп величина интервала будет минимальна. Число групп в вариационном ряду можно найти по формуле Стерджеса:  (k-число групп, n - объем выборки), а ширину интервала –
(k-число групп, n - объем выборки), а ширину интервала – 
где  - максимальное;
- максимальное; 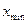 - минимальное значения вариант, а их разность R носит название размаха вариации.
- минимальное значения вариант, а их разность R носит название размаха вариации.
Исследуется выборка из 100 человек из совокупности всех студентов медицинского ВУЗа.
Решение: Рассчитаем число групп: 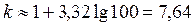 . Таким образом, для составления интервального ряда данную выборку лучше разбить на 7 или 8 групп. Совокупность групп, на которые разбиваются результаты наблюдений и частот получения результатов наблюдений в каждой группе, называют статистической совокупностью.
. Таким образом, для составления интервального ряда данную выборку лучше разбить на 7 или 8 групп. Совокупность групп, на которые разбиваются результаты наблюдений и частот получения результатов наблюдений в каждой группе, называют статистической совокупностью.
Для наглядного представления статистического распределения пользуются гистограммой.
Гистограмма частот – это ступенчатая фигура, состоящая из смежных прямоугольников, построенных на одной прямой, основания которых одинаковы и равны ширине интервала, а высота равна или частоте попадания в интервал 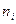 или относительной частоте ωi.
или относительной частоте ωi.
Наблюдения за числом частиц, попавших в счетчик Гейгера, в течение минуты дали следующие результаты:
21 30 39 31 42 34 36 30 28 30 33 24 31 40 31 33 31 27 31 45 31 34 27 30 48 30 28 30 33 46 43 30 33 28 31 27 31 36 51 34 31 36 34 37 28 30 39 31 42 37.
Построить по этим данным интервальный вариационный ряд с равными интервалами (I интервал 20-24; II интервал 24-28 и т.д.) и начертить гистограмму.
Решение: n=50
| Интервал | 20-24 | 24-28 | 28-32 | 32-36 | 36-40 | 40-44 | 44-48 | 48-52 |
Частота 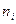
|
Гистограмма этого распределения имеет вид:

Рис. 13.2. Гистограмма распределения
Варианты заданий
№13.1.Через каждый час измерялось напряжение тока в электросети. При этом были получены следующие значения (В):
227 219 215 230 232 223 220 222 218 219 222 221 227 226 226 209 211 215 218 220 216 220 220 221 225 224 212 217 219 220.
Построить статистическое распределение и начертить полигон.
№13.2.Наблюдения за сахаром крови у 50 человек дали такие результаты:
3.94 3.84 3.86 4.06 3.67 3.97 3.76 3.61 3.96 4.04
3.82 3.94 3.98 3.57 3.87 4.07 3.99 3.69 3.76 3.71
3.81 3.71 4.16 3.76 4.00 3.46 4.08 3.88 4.01 3.93
3.92 3.89 4.02 4.17 3.72 4.09 3.78 4.02 3.73 3.52
3.91 3.62 4.18 4.26 4.03 4.14 3.72 4.33 3.82 4.03
Построить по этим данным интервальный вариационный ряд с равными интервалами (I - 3.45-3.55; II - 3.55-3.65 и т. д.) и изобразить его графически, начертить гистограмму.
№13.3.Построить полигон частот распределения скорости оседания эритроцитов (СОЭ) у 100 человек:

| |||||
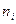
|
№13.4.Построить гистограмму распределения скорости оседания эритроцитов (СОЭ) у 50 человек:
| Интервал | 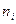
|
| 2-5 | |
| 5-8 | |
| 8-11 | |
| 11-14 |
Статистические оценки параметров распределения. Выборочные характеристики
Характеристики положения
Мода () – это такое значение варианты, что предшествующее и следующее за ним значения имеют меньшие частоты встречаемости или =, такое, что n() =… Для одномодальных распределений мода – это наиболее часто встречающаяся… Например, для распределения: …Характеристики рассеяния вариант вокруг своего среднего
Выборочная дисперсия – среднее арифметическое квадратов отклонения вариант от их среднего значения:
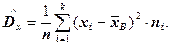 Исправленная дисперсия при малых выборках n<30
Исправленная дисперсия при малых выборках n<30 
Среднее квадратическое отклонение – это квадратный корень из выборочной дисперсии:
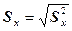 – исправленное значение (n<30).
– исправленное значение (n<30). 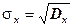
Коэффициент вариации СV – это отношение среднего квадратического отклонения к средней величине признака, выраженное в процентах:

Коэффициент вариации – это мера относительной изменчивости случайной величины, которая позволяет сравнивать разнородные величины, например, частоту сердечных сокращений (ЧСС, уд/мин), артериальное давление (АД, мм. рт. ст.) и температуру (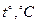 ) в единых единицах - процентах.
) в единых единицах - процентах.
Пример 4.
Выборочная совокупность задана таблицей распределения:

| ||||
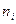
|
Найти выборочную дисперсию. Решение: Найдем выборочную среднюю:
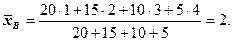
Найдем выборочную дисперсию:
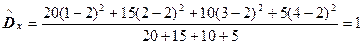
Сравните 2 варьирующихся признака. Один характеризуется средней 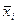 = 2,4 кг и средним квадратическим отклонением
= 2,4 кг и средним квадратическим отклонением 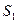 = 0,58 кг, другой - величинами
= 0,58 кг, другой - величинами 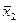 = 8,3 см и
= 8,3 см и 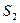 = 1,57 см. Какой признак варьируется сильнее?
= 1,57 см. Какой признак варьируется сильнее?
Решение:

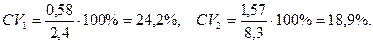
Ответ: первый, так как 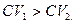 .
.
Варианты заданий
Найти выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение, если совокупность задана таблицей распределения:
№ 13.1.
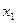
| |||
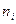
|
№ 13.2.

| ||||
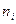
|
№ 13.3.

| ||||
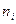
|
№ 13.4.

| |||||||
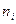
|
№ 13.5.

| 6,68 | 6,70 | 6,72 | 6,74 |
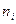
|
№ 13.6.

| 6,76 | 6,78 | 6,80 | 6,82 | 6,84 |
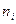
|
Оценка параметров генеральной совокупности по ее выборке
Числовые значения, характеризующие генеральную совокупность, называются… Статистическое оценивание может выполняться двумя способами:Точечная оценка параметров генеральной совокупности
Качество оценки устанавливается по трем свойствам: быть состоятельной, эффективной и несмещенной. Точечная оценка называется состоятельной, если при увеличении объема выборки… Точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с…Варианты заданий
№ 13.1. При исследовании клинической оценки тяжести серповидноклеточной анемии была получена выборка объема 33.
0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 3; 4; 4; 5;
5;5;5;6;7;9;10;11.
Найдите среднюю, среднее квадртическое отклонение и
медиану. Можно ли считать, что выборка извлечена из
совокупности с нормальным распределением?
№ 13.2. Исследуя продолжительность (в секундах) физической нагрузки до развития приступа стенокардии у 12 человек с ишемической болезнью сердца, получили следующие данные:
289;203; 359; 243; 232; 210; 215; 246; 224; 239; 220; 211. Найдите среднюю, среднее квадратическое отклонение, медиану. Можно ли считать, что данная выборка извлечена из совокупности с нормальным распределением?
№ 13.3. Найдите среднее число очков, выпадающих при бросании игральной кости. Опишите это распределение. Может ли оно быть нормальным?
Интервальная оценка параметров генеральной совокупности
Интервальная оценка – это числовой интервал, который определяется двумя числами-границами интервала, содержащий неизвестный параметр генеральной… Доверительный интервал – это интервал, в котором с той или иной заранее… Доверительная вероятность р - это такая вероятность, что событие вероятности (1 - р) можно считать невозможным. - это…Варианты заданий
№ 13.1. При исследовании частоты дыхания по выборке объема n = 15 были получены выборочная средняя  =18,5 и среднее квадратическое отклонение S = 0,6. Определить интервальную оценку математического ожидания с вероятностью
=18,5 и среднее квадратическое отклонение S = 0,6. Определить интервальную оценку математического ожидания с вероятностью  .
.
№ 13.2. Найти доверительный интервал для оценки с уровнем доверительной вероятности  неизвестного математического ожидания нормального распределения признака х – диаметра эритроцита – генеральной совокупности, если выборочная средняя
неизвестного математического ожидания нормального распределения признака х – диаметра эритроцита – генеральной совокупности, если выборочная средняя  =10,2 мкм; исправленное выборочное среднее квадратическое отклонение S = 4 и объем выборки п = 16. 16. При исследовании эффективности диуретика было установлено, что среднее увеличение диуреза в группе из n=10 человек составило
=10,2 мкм; исправленное выборочное среднее квадратическое отклонение S = 4 и объем выборки п = 16. 16. При исследовании эффективности диуретика было установлено, что среднее увеличение диуреза в группе из n=10 человек составило  . Найти доверительный интервал (
. Найти доверительный интервал ( ) для среднего изменения диуреза, если ошибка выборочной средней
) для среднего изменения диуреза, если ошибка выборочной средней 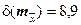 .
.
№ 13.3. При исследовании проницаемости сосудов сетчатки для выборки объемом n = 25 были получены следующие данные: выборочная средняя  = 14, среднее квадратическое отклонение S=5. Считая, что данный признак х распределен нормально, найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания.
= 14, среднее квадратическое отклонение S=5. Считая, что данный признак х распределен нормально, найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания.
№ 13.4. Определить доверительный интервал для средней активности препарата с уровнем доверительной вероятности  .
.
х: 905,925,940,961,974, 995.
№ 13.5. С доверительной вероятностью  определить для количества крови, протекающего за 1 минуту через почки, если выборочная средняя
определить для количества крови, протекающего за 1 минуту через почки, если выборочная средняя  = 1300мл крови, а ошибка выборочной средней
= 1300мл крови, а ошибка выборочной средней  =30 мл. Объем выборки n = 12.
=30 мл. Объем выборки n = 12.
Контрольные вопросы
1. Перечислить основные понятия математической статистики.
2. Каким образом строится полигон частот и гистограмма.
3. Что называют вариантой, вариационным рядом и относительной частотой.
4. Перечислить формы вариационного ряда.
5. Перечислить статистические оценки параметров распределения.
6. Определение статистической оценки неизвестного параметра.
7. Какая оценка называется точечной?
8. Каким требованиям должны удовлетворять статистические оценки?
9. Сформулировать определения генеральной средней и генеральной дисперсии.
10. Записать выражения для вычисления выборочной средней, выборочной дисперсии и исправленной дисперсии. Какая из этих оценок не является несмещенной?
11. Методики вычисления границ доверительного интервала для оценки математического ожидания нормально распределенной СВ при известном и неизвестном s.
12. Методика вычисления границ доверительного интервала для оценки среднего квадратического отклонения нормально распределенной СВ.
Глава 14. Корреляционный и регрессионный анализ
Корреляционный анализ - это статистический метод, изучающий связь между явлениями, если одно из них входит в число причин, определяющих другое, или, если имеются общие причины, воздействующие на эти явления.
Основная задача - выявление связи между случайными переменными.
Регрессионный анализ - это статистический метод, изучающий зависимость между результативным признаком Y и входной переменной X.
Основная задача - установление формы связи между переменными и изучение зависимости между ними.
Функциональная и корреляционная зависимости
Корреляционная зависимость - это статистическая зависимость, проявляющаяся в том, что при изменении одной из величин изменяется среднее значение… . Например, рост и масса. При одном и том же росте масса различных индивидуумов может быть различна, но между средними…А б
Рис. 14.1. Поле корреляции
Если точки группируются вдоль некоторого направления (рис. 14.1а), то это говорит о наличии линейной корреляционной связи между признаками.
Если точки распределены равномерно (рис. 14.1б), то линейная корреляционная связь отсутствует.
На рисунке 13.2 приведены примеры зависимостей Y от X и отдельно даны значения коэффициента корреляции r. Найти соответствие между значениями коэффициента корреляции и графиками зависимостей.
Значения r:
1) 1; 2) 0,8; 3) 0; 4) -1.
Эталон ответа: 1...; 2...; 3...; 4....
Примеры зависимостей:

Рис. 14.2.Корреляционные поля точек
Ответ: 14.2а; 14.2в; 14.2г; 14.4б.
Коэффициент линейной корреляции и его свойства
Требования к корреляционному анализу: корреляционный анализ - это метод, используемый, когда данные можно считать случайными и выбранными из… Выборочный коэффициент линейной корреляции r характеризует тесноту линейной… .Свойства коэффициента корреляции r.
1. Коэффициент корреляции принимает значения на отрезке -1 ≤ r ≤ 1. В зависимости от того, насколько |r| приближается к 1, различают… r < 0,3 - слабая связь; r = 0,3-0,5 - умеренная связь;Проверка гипотезы о значимости выборочного коэффициента линейной корреляции
Эмпирический коэффициент корреляции, как и любой другой выборочный показатель, служит оценкой своего генерального параметра. Выборочный коэффициент… Чтобы выяснить, находятся ли случайные величины X и Y генеральной совокупности… Критерием для проверки нулевой гипотезы является отношение выборочного коэффициента корреляции к своей ошибке:Выборочное уравнение линейной регрессии. Метод наименьших квадратов
В них могут быть завуалированы некоторые соотношения, основные черты которых и позволяют выявлять методы регрессионного анализа. При этом задача регрессионного анализа состоит в подборе упрощенной… Регрессионный анализ имеет в своем распоряжении специальные процедуры проверки, является ли выбранная математическая…Нелинейная регрессия
Выбор вида уравнения регрессии производится на основании опыта предыдущих исследований, литературных источников, профессионального мнения и… Наиболее часто встречаются следующие виды уравнений нелинейной регрессии: - полиномиальное уравнение;Варианты заданий
► Провести корреляционно-регрессионный анализ:
построить корреляционное ноле точек;
проверить значимость (α ≤ 0,05) коэффициента корреляции между переменными Х и Y;
построить линию регрессии.
№ 14.1.Изучали зависимость между содержанием коллагена Y и эластина X в магистральных артериях головы (г/100 г сухого вещества, возраст 36-50 лет).
Результаты наблюдений приведены в виде двумерной выборки объема 5:
| xi: | 13,98 | 15,84 | 7,26 | 7,74 | 8,82; |
| yi: | 35,50 | 42,82 | 47,79 | 43,29 | 49,47. |
Результаты расчета на компьютере:
r = - 0,85; тr = 0,3; tнабл = 2,84;  = -1,04 х + 58,97.
= -1,04 х + 58,97.
№ 14.2.Изучали зависимость между содержанием коллагена Y и эластина Х в магистральных артериях головы (г/100 г сухого вещества, возраст 51-75 лет).
Результаты наблюдений приведены в виде двумерной выборки объема 5:
| xi: | 13,50 | 13,09 | 6,45 | 7,26 | 8,80; |
| yi: | 33,97 | 38,07 | 53,98 | 46,00 | 48,61. |
Результаты расчета на компьютере:
r = -0,94; mr = 0,2; tнабл = 4,8;  = -2,3 х + 66,8.
= -2,3 х + 66,8.
№ 14.3.Изучали зависимость между систолическим давлением Y (мм рт. ст.) у мужчин в начальной стадии шока и возрастом X (годы). Результаты наблюдений приведены в виде двумерной выборки объема 11:
| xi: | 54; | ||||||||||
| yi: | 124. |
Результаты расчета на компьютере:
r = -0,61; mr = 0,283; tнабл = 2,3;  = -0,8 х + 177,8.
= -0,8 х + 177,8.
№ 13.6.4.Имеется двумерная выборка объемом 9: X - масса новорожденных павианов-гамадрилов (кг) и Y - масса их матерей (кг).
| xi: | 0,7 | 0,73 | 0,75 | 0,70 | 0,65 | 0,70 | 0,61 | 0,70 | 0,63; |
| yi: | 10,8 | 11,3 | 11,1 | 11,3 | 10,2 | 13,5 | 12. |
Результаты расчета на компьютере:
r = 0,02; mr = 0,38; tнабл = 0,05;  = 0,43 х + 10,87.
= 0,43 х + 10,87.
№ 14.5.Изучали зависимость между суточной выработкой продукции на медицинском предприятии Y (т) и величиной основных производственных фондов X (млн руб).
Результаты наблюдений приведены в виде двумерной выборки объема 5:
| xi: | 25,5 | 29,5 | 31,9 | 35,4 | 39,2; |
| yi: | 25. |
Результаты расчёта на компьютере:
r = 0,74; tнабл = 7,62;  = 0,67 х – 4,79.
= 0,67 х – 4,79.
№ 14.6.Изучали зависимость между объемом валовой продукции Y (млн руб) и среднесуточной численностью рабочих X. Результаты наблюдений приведены в виде двумерной выборки объема 5:
| xi: | 5,5 | 8; | |||
| yi: | 50. |
Результаты расчета на компьютере:
r = 0,8; tнабл = 6,2;  = 3,2 х + 22,4.
= 3,2 х + 22,4.
№ 14.7.Изучали зависимость между минутным объемом сердца Y (л/мин) и средним давлением в левом предсердии X (см рт. ст.). Результаты наблюдений приведены в виде двумерной выборки объема 5:
| xi: | 4,8 | 6,4 | 9,3 | 11,2 | 17,7; |
| yi: | 0,4 | 0,69 | 1,29 | 1,64 | 2,4. |
Результаты расчета на компьютере:
r = 0,989; mr = 0,084; tнабл = 11,7;  = 0,15 х – 0,25.
= 0,15 х – 0,25.
№ 14.8.Изучали зависимость между объемом Y (мкм3) и диаметром Х (мкм) сухого эритроцита у млекопитающих. Результаты наблюдений приведены в виде двумерной выборки объема 9:
| xi: | 7,6 | 8,9 | 5,5 | 9,2 | 3,5 | 4,8 | 7,3 | 7,4 | 6,8; |
| yi: | 54. |
Результаты расчета на компьютере:
r = 0,96; mr = 0,12; tнабл = 7,99;  = 14,28 х – 32,5.
= 14,28 х – 32,5.
№ 14.9.Изучали зависимость между количеством гемоглобина в крови (%) Y и массой животных X (кг). Результаты наблюдений приведены в виде двумерной выборки объема 9:
| xi: | 17,7 | 30; | |||||||
| yi: | 86. |
Результаты расчета на компьютере:
r = 0,64; mr = 0,29; tнабл = 2,2;  = 1,04 х + 56,95.
= 1,04 х + 56,95.
№ 14.10.Изучали зависимость между массой тела гамадрилов-матерей X (кг) и их новорожденных детенышей Y (кг). Под наблюдением находилось 20 обезьян.
| xi: | 10,8 | 11,3 | 10,1 | 11,1 | 11,3 | 10,2 | 13,5 | 12,3 | ||
| 14,5 | 11,8 | 13,4 | 11,4 | 15,5 | 12,1; | |||||
| yi: | 0,7 | 0,73 | 0,75 | 0,7 | 0,65 | 0,65 | 0,7 | 0,61 | 0,7 | 0,63 |
| 0,7 | 0,65 | 0,72 | 0,69 | 0,78 | 0,7 | 0,6 | 0,85 | 0,8 | 0,75. |
Результаты расчета на компьютере:
r = 0,564; mr = 0,2; tнабл = 2,9;  = 0,024 х + 0,42.
= 0,024 х + 0,42.
 № 14.11.Изучали зависимость между содержанием коллагена Y и эластина X в магистральных артериях головы (г/100 г сухого вещества, возраст 21-35 лет).
№ 14.11.Изучали зависимость между содержанием коллагена Y и эластина X в магистральных артериях головы (г/100 г сухого вещества, возраст 21-35 лет).
Результаты наблюдений приведены в виде двумерной выборки объема 5:
| xi: | 14,9 | 16,72 | 7,73 | 9,9 | 8,84; |
| yi: | 40,18 | 44,57 | 52,93 | 47,77 | 49,07. |
Результаты расчета на компьютере:
r = -0,85; mr = 0,3; tнабл = 2,84;  = -1,04 х + 58,97.
= -1,04 х + 58,97.
№ 14.12.Изучали зависимость между площадью поверхности тела Y (м2) и ростом женщин Х (см). Результаты наблюдений приведены в виде двумерной выборки объема 11:
| xi: | 161; | ||||||||||
| yi: | 1,74 | 1,74 | 1,67 | 1,51 | 1,52 | 1,55 | 1,58 | 1,58 | 1,44 | 1,67 | 1,42. |
Результаты расчета на компьютере:
r = 0,145; mr = 0,4; tнабл = 0,44;  = 0,001 х + 1,23.
= 0,001 х + 1,23.
№ 14.13.Изучали зависимость между поверхностью Y (мкм2) и диаметром X (мкм) сухого эритроцита у млекопитающих.
Результаты наблюдений приведены в виде двумерной выборки объема 9:
| xi: | 7,6 | 8,9 | 5,5 | 9,2 | 3,5 | 4,8 | 7,3 | 7,4 | 6,8; |
| yi: | 144. |
Результаты расчета на компьютере:
r = 0,95; mr = 0,11; tнабл = 8,53;  = 27,9 х – 60,63.
= 27,9 х – 60,63.
Приложение
T-распределение (распределение Стьюдента)
Таблица 1 k Односторонняя критическая область (a) …Точные и асимптотические границы для верхней грани модуля разности
Истинной и эмпирической функции распределения
При n > 100 следует принять асимптотические границы для которых истинные коэффициенты доверия несколько больше заданных величин 0,95 и 0,99 соответственно.Таблица 5
| n | Вероятность | ||||||||||
| 0,999 | 0,995 | 0,99 | 0,98 | 0,975 | 0,95 | 0,90 | 0,80 | 0,75 | 0,70 | 0,50 | |
| 0,05157 0,00200 0,0243 0,0908 0,210 0,381 0,598 0,857 1,152 1,479 1,834 2,214 2,617 3,041 3,483 3,942 4,416 4,905 5,407 5,921 6,447 6,983 7,529 8,035 8,649 9,222 9,803 10,391 10,986 11,588 | 0,04393 0,0100 0,0717 0,207 0,412 0,676 0,989 1,344 1,735 2,156 2,603 3,074 3,565 4,075 4,601 5,142 5,697 6,265 6,844 7,434 8,034 8,643 9,260 9,886 10,520 11,160 11,808 12,461 13,121 13,787 | 0,03157 0,0201 0,115 0,297 0,554 0,872 1,239 1,646 2,088 2,558 3,053 3,571 4,107 4,660 5,229 5,812 6,408 7,015 7,633 8,260 8,897 9,542 10,196 10,856 11,524 12,198 12,879 13,565 14,256 14,953 | 0,03628 0,0404 0,185 0,429 0,752 1,134 1,564 2,032 2,532 3,059 3,609 4,178 4,765 5,368 5,985 6,614 7,255 7,906 8,567 9,237 9,915 10,600 11,293 11,992 12,697 13,409 14,125 14,847 15,574 16,306 | 0,03982 0,0506 0,216 0,484 0,831 1,237 1,690 2,180 2,700 3,247 3,816 4,404 5,009 5,629 6,262 6,908 7,564 8,231 8,907 9,591 10,283 10,982 11,688 12,401 13,120 13,844 14,573 15,308 16,047 16,791 | 0,0093 0,103 0,352 0,711 1,145 1,635 2,167 2,733 3,325 3,240 4,575 5,226 5,892 6,571 7,261 7,962 8,672 9,390 10,117 10,871 11,591 12,338 13,091 13,848 14,611 15,379 16,151 16,928 17,708 18,493 | 0,0158 0,211 0,584 1,064 1,610 2,204 2,833 3,490 4,168 4,865 5,578 6,304 7,042 7,790 8,547 9,312 10,085 10,865 11,651 12,443 13,240 14,041 14,848 15,659 16,173 17,292 18,114 18,937 19,768 20,599 | 0,0642 0,446 1,005 1,649 2,343 3,070 3,822 4,594 5,380 6,179 6,989 7,807 8,634 9,467 10,307 11,152 12,002 12,857 13,716 14,578 15,445 16,314 17,187 18,062 18,940 19,830 20,703 21,588 22,475 23,364 | 0,102 0,575 1,213 1,923 2,675 3,455 4,255 5,071 5,899 6,787 7,584 8,438 9,299 10,165 11,036 11,912 12,892 13,675 14,562 15,452 16,344 17,240 18,137 19,037 19,939 20,843 21,749 22,657 23,567 24,478 | 0,148 0,713 1,424 2,195 3,000 3,828 4,671 5,527 6,393 7,267 8,148 9,034 9,926 10,821 11,721 12,624 13,531 14,440 15,352 16,266 17,182 18,101 19,021 19,943 20,887 21,792 22,719 23,617 24,577 25,508 | 0,455 1,386 2,366 3,357 4,351 5,348 6,346 7,344 8,343 9,342 10,341 11,340 12,340 13,339 14,339 15,338 16,338 17,338 18,338 19,337 20,337 21,337 22,337 23,337 24,337 25,336 26,136 27,386 28,336 29,336 |
Таблица 6
| n | Вероятность | |||||||||
| 0,30 | 0,25 | 0,20 | 0,10 | 0,05 | 0,025 | 0,02 | 0,01 | 0,005 | 0,001 | |
| 1,074 2,408 3,665 4,878 6,064 7,231 8,383 9,524 10,656 11,781 12,899 14,011 15,119 16,222 17,322 18,418 19,511 20,601 21,689 22,775 23,858 24,939 26,018 27,096 28,172 29,246 30,319 31,391 32,461 33,530 | 1,323 2,773 4,108 5,385 6,626 7,841 9,037 10,219 11,389 12,549 13,701 14,845 15,984 17,117 18,245 19,369 20,489 21,605 22,718 23,828 24,935 26,039 27,141 28,241 29,339 30,434 31,528 32,620 33,711 34,800 | 1,642 3,219 4,642 5,989 7,289 8,558 9,803 11,030 12,242 13,412 14,631 15,812 16,985 18,151 19,311 20,465 21,615 22,760 23,900 25,038 26,171 28,429 29,553 30,675 31,795 32,912 34,027 35,139 36,250 | 2,706 4,605 6,251 7,779 9,236 10,645 12,017 13,362 14,684 15,987 17,275 18,549 19,812 21,064 22,307 23,542 24,769 25,989 27,204 28,412 29,615 30,813 32,007 33,196 34,328 35,563 36,741 37,916 39,087 40,256 | 3,841 5,991 7,815 9,488 11,070 12,592 14,067 15,507 16,919 18,307 19,675 21,026 22,362 23,685 24,996 26,296 27,587 28,869 30,144 31,410 32,671 33,924 35,172 36,415 37,652 38,885 40,113 41,337 42,557 43,773 | 5,024 7,378 9,348 11,143 12,839 14,449 16,013 17,535 19,023 20,483 21,920 23,337 24,736 26,119 27,488 28,845 30,191 31,526 32,852 34,170 35,479 36,781 38,076 39,364 40,046 41,923 43,194 44,461 45,722 46,979 | 5,412 7,824 9,837 11,668 13,388 15,033 16,622 18,168 19,679 21,161 22,618 24,054 25,472 26,873 28,259 29,633 30,995 32,346 33,687 35,020 36,343 37,659 38,968 40,270 41,566 42,856 44,140 45,419 46,693 47,962 | 6,635 9,210 11,345 13,277 15,086 16,812 18,475 20,090 21,666 23,209 24,725 26,217 27,688 29,141 30,578 32,000 33,409 34,805 36,191 37,566 38,932 40,289 41,638 42,980 44,314 45,642 46,963 48,278 49,588 50,892 | 7,879 10,597 12,838 14,860 16,750 18,548 20,278 21,955 23,589 25,188 26,757 28,300 29,819 31,319 32,801 34,267 35,718 37,156 38,582 39,997 41,401 42,796 44,181 45,558 46,928 48,290 49,645 50,993 52,336 53,672 | 10,827 13,815 16,268 18,465 20,517 22,457 24,322 26,125 27,877 29,588 31,264 32,909 34,528 36,123 37,697 39,252 40,790 42,312 43,820 45,315 46,797 48,268 49,728 51,170 52,620 54,052 55,476 56,893 58,302 59,703 |
Распределение Фишера – Снедекора (F-распределение)
Значения Fтабл, удовлетворяющие условию P(F > Fтабл). Первое значение соответствует вероятности 0,05; второе – вероятности 0,01 и третье – вероятности 0,001; n1 – число степеней свободы числителя; n2 – знаменателя
Таблица 7
| n1 n2 | ¥ | t | |||||||||
| 161,4 18,51 98,49 998,46 10,13 34,12 67,47 7,71 21,20 74,13 6,61 16,26 47,04 5,99 13,74 35,51 5,59 12,25 29,22 5,32 11,26 25,42 5,12 10,56 22,86 4,96 10,04 21,04 | 199,5 19,00 99,01 999,00 9,55 30,81 148,51 6,94 18,00 61,24 5,79 13,27 36,61 5,14 10,92 26,99 4,47 9,55 21,69 4,46 8,65 18,49 4,26 8,02 16,39 4,10 7,56 14,91 | 215,7 19,16 99,17 999,20 9,28 29,46 141,10 6,59 16,69 56,18 5,41 12,06 33,20 4,76 9,78 23,70 4,35 8,45 18,77 4,07 7,59 15,83 3,86 6,99 13,90 3,71 6,55 12,55 | 224,6 19,25 99,25 999,20 9,12 28,71 137,10 6,39 15,98 5,19 11,39 31,09 4,53 9,15 21,90 4,12 7,85 17,19 3,84 7,10 14,39 3,63 6,42 12,56 3,48 5,99 11,28 | 230,2 19,30 99,30 999,20 9,01 28,24 134,60 6,26 15,52 51,71 5,05 10,97 20,75 4,39 8,75 20,81 3,97 7,46 16,21 3,69 6,63 13,49 3,48 6,06 11,71 3,33 5,64 10,48 | 234,0 19,33 99,33 999,20 8,94 27,91 132,90 6,16 15,21 50,52 4,95 10,67 28,83 4,28 8,47 20,03 3,87 7,19 15,52 3,58 6,37 12,86 3,37 5,80 11,13 3,22 5,39 9,92 | 238,9 19,37 99,36 999,40 8,84 27,49 130,60 6,04 14,80 49,00 4,82 10,27 27,64 4,15 8,10 19,03 3,73 6,84 14,63 3,44 6,03 12,04 3,23 5,47 10,37 3,07 5,06 9,20 | 243,9 19,41 99,42 999,60 8,74 27,05 128,30 5,91 14,37 47,41 4,68 9,89 26,42 4,00 7,72 17,99 3,57 6,47 13,71 3,28 5,67 11,19 3,07 5,11 9,57 2,91 4,71 8,45 | 249,0 19,45 99,46 999,40 8,64 26,60 125,90 5,77 13,93 45,77 4,53 9,47 25,14 3,84 7,31 16,89 3,41 6,07 12,73 3,12 5,28 10,30 2,90 4,73 8,72 2,74 4,33 7,64 | 253,3 19,50 99,50 999,40 8,53 26,12 123,50 5,63 13,46 44,05 4,36 9,02 23,78 3,67 6,88 15,75 3,23 5,65 11,70 2,99 4,86 9,35 2,71 4,31 7,81 2,54 3,91 6,77 | 12,71 63,66 636,2 4,30 9,92 31,00 3,18 5,84 12,94 2,78 4,60 8,61 2,57 4,03 6,86 2,45 3,71 5,96 2,36 3,50 5,40 2,31 3,36 5,04 2,26 3,25 4,78 2,23 3,17 4,59 |
Продолжение таблицы 7
| n1 n2 | ¥ | t | |||||||||
| 4,84 9,65 19,69 4,75 9,33 18,64 4,67 9,07 17,81 4,60 8,86 17,14 4,45 8,68 16,59 4,41 8,53 16,12 4,45 8,40 15,72 4,41 8,28 15,38 4,38 8,18 15,08 4,35 8,10 14,82 4,32 8,02 14,62 4,30 7,94 14,38 | 3,98 7,20 13,81 3,88 6,93 12,98 3,80 6,70 12,31 3,74 6,51 11,78 3,68 6,36 11,34 3,63 6,23 10,97 3,59 6,11 10,66 3,55 6,01 10,39 3,52 5,93 10,16 3,49 5,85 9,95 3,47 5,78 9,77 3,44 5,72 9,61 | 3,59 6,22 11,56 3,49 5,95 10,81 3,41 5,74 10,21 3,34 5,56 9,73 3,29 5,42 9,34 3,24 5,29 9,01 3,20 5,18 8,73 3,16 5,09 8,49 3,13 5,01 8,28 3,10 4,94 8,10 3,07 4,87 7,94 3,05 4,82 7,80 | 3,36 5,67 10,35 3,26 5,41 9,63 3,18 5,20 9,07 3,11 5,03 8,62 3,06 4,89 8,25 3,01 4,77 7,94 2,96 4,67 7,68 2,93 4,58 7,46 2,90 4,50 7,26 2,87 4,43 7,10 2,84 4,37 6,95 2,82 4,31 6,87 | 3,20 5,32 9,58 3,11 5,06 8,89 3,02 4,86 8,35 2,96 4,69 7,92 2,90 4,56 7,57 2,85 4,44 7,27 2,81 4,34 7,02 2,77 4,25 6,81 2,74 4,17 6,61 2,71 4,10 6,46 2,68 4,04 6,32 2,66 3,99 6,19 | 3,09 5,07 9,05 3,00 4,82 8,38 2,92 4,62 7,86 2,85 4,46 7,44 2,79 4,32 7,09 2,74 4,20 6,80 2,70 4,10 6,56 2,66 4,01 6,35 2,63 3,94 6,18 2,60 3,87 6,02 2,57 3,81 5,88 2,55 3,75 5,76 | 2,95 4,47 8,35 2,85 4,50 7,71 2,77 4,30 7,21 2,70 4,14 6,80 2,64 4,00 6,47 2,59 3,89 6,20 2,55 3,79 5,96 2,51 3,71 5,76 2,48 3,63 5,59 2,45 3,56 5,44 2,42 3,51 5,31 2,40 3,45 5,19 | 2,79 4,40 7,62 2,69 4,16 7,00 2,60 3,96 6,52 2,53 3,80 6,13 2,48 3,67 5,81 2,42 3,55 5,55 2,38 3,45 5,32 2,34 3,37 5,13 2,31 3,30 4,97 2,28 3,23 4,82 2,25 3,17 4,70 2,23 3,12 4,58 | 2,61 4,02 6,85 2,50 3,78 6,25 2,42 3,59 5,78 2,35 3,43 5,41 2,29 3,29 5,10 2,24 3,18 4,85 2,19 3,08 4,63 2,15 3,01 4,45 2,11 2,92 4,29 2,08 2,86 4,15 2,05 2,80 4,03 2,03 2,75 3,92 | 2,40 3,60 6,00 2,30 3,36 5,42 2,21 3,16 4,97 2,13 3,00 4,60 2,07 2,87 4,31 2,01 2,75 4,06 1,96 2,65 3,85 1,92 2,57 3,67 1,88 2,49 3,52 1,84 2,42 3,38 1,82 2,36 3,26 1,78 2,30 3,15 | 2,20 3,11 4,49 2,18 3,06 4,32 2,16 3,01 4,12 2,14 2,98 4,14 2,13 2,95 4,07 2,12 2,92 4,02 2,11 2,90 3,96 2,10 2,88 3,92 2,09 2,86 3,88 2,09 2,84 3,85 2,08 2,83 3,82 2,07 2,82 3,79 |
Продолжение таблицы 7
| n1 n2 | ¥ | t | |||||||||
| ¥ | 4,28 7,88 14,19 4,26 7,82 14,03 4,24 7,77 13,88 4,22 7,72 13,74 4,21 7,68 13,61 4,19 7,64 13,50 4,18 7,60 13,39 4,17 7,56 13,29 4,00 7,08 11,97 3,84 6,64 10,83 | 3,42 5,66 9,46 3,40 5,61 9,34 3,38 5,57 9,22 3,37 5,53 9,12 3,35 5,49 9,02 3,34 5,45 8,93 3,33 5,42 8,85 3,32 5,39 8,77 3,15 4,98 7,76 2,99 4,60 6,91 | 3,03 4,76 7,67 3,01 4,72 7,55 2,99 4,68 7,45 2,98 4,64 7,36 2,96 4,60 7,27 2,95 4,57 7,18 2,93 4,54 7,12 2,92 4,51 7,05 2,76 4,13 6,17 2,60 3,78 5,42 | 2,80 4,26 6,70 2,78 4,22 6,59 2,76 4,18 6,49 2,74 4,14 6,41 2,73 4,11 6,33 2,71 4,07 6,25 2,70 4,04 6,19 2,69 4,02 6,12 2,52 3,65 5,31 2,37 3,32 4,62 | 2,46 3,94 6,08 2,62 3,90 5,98 2,60 3,86 5,89 2,59 3,82 5,80 2,57 3,78 5,73 2,56 3,75 5,66 2,54 3,73 5,59 2,53 3,70 5,53 2,37 3,34 4,76 2,21 3,02 4,10 | 2,53 3,71 5,56 2,51 3,67 5,55 2,49 3,63 5,46 2,47 3,59 5,38 2,46 3,56 5,31 2,44 3,53 5,24 2,43 3,50 5,18 2,42 3,47 5,12 2,25 3,12 4,37 2,09 2,80 3,74 | 2,38 3,41 5,09 2,36 3,36 4,99 2,34 3,32 4,91 2,32 3,29 4,83 2,30 3,26 4,76 2,29 3,23 4,69 2,28 3,20 4,65 2,27 3,17 4,58 2,10 2,82 3,87 1,94 2,51 3,27 | 2,20 3,07 4,48 2,18 3,03 4,39 2,16 2,99 4,31 2,15 2,96 4,24 2,13 2,93 4,17 2,12 2,90 4,11 2,10 2,87 4,05 2,09 2,84 4,00 1,92 2,50 3,31 1,75 2,18 2,74 | 2,00 2,70 3,82 1,98 2,66 3,84 1,96 2,62 3,66 1,95 2,58 3,59 1,93 2,55 3,52 1,91 2,52 3,46 1,90 2,49 3,41 1,89 2,47 3,36 1,70 2,12 2,76 1,52 1,79 2,13 | 1,76 2,26 3,05 1,73 2,21 2,97 1,71 2,17 2,89 1,69 2,13 2,82 1,67 2,10 2,76 1,65 2,06 2,70 1,64 2,03 2,64 1,62 2,01 2,59 1,39 1,60 1,90 1,03 1,04 1,05 | 2,07 2,81 3,77 2,06 2,80 3,75 2,06 2,79 3,72 2,06 2,78 3,71 2,05 2,77 3,69 2,05 2,76 3,67 2,05 2,76 3,66 2,04 2,75 3,64 2,00 2,66 3,36 1,96 2,58 3,29 |
Библиографический список
1. Баврин И.И. Высшая математика: учеб. для студ. высш. учеб. заведений /И.И. Баврин, В.Л. Матросов. – М.: Владос, 2002. –400с. 2. Берман Г.Н. Сборник задач по курсу математического анализа: учеб. пособие… 3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для…Содержание
Глава 1. Предел функции. 3
1.1. Определение предела. 3
1.2. Операции над пределами. 4
1.3. Замечательные пределы.. 5
1.4. Примеры.. 6
1.5. Варианты заданий. 8
1.6. Контрольные вопросы.. 10
Глава 2. Производная и дифференциал. 10
2.1 Понятие производной. 10
2.2. Геометрический и физический смысл производной. 10
2.3. Таблица производных. 12
2.4. Основные правила дифференцирования. 12
2.5. Производные высших порядков. 13
2.6. Дифференциал функции. 13
2.7. Геометрический смысл и свойства дифференциала. 14
2.8. Дифференциалы высших порядков. 15
2.9. Примеры.. 15
2.10. Варианты заданий. 17
Глава 3. Исследование функций и построение графиков. 21
3.1. Промежутки монотонности и знакопостоянства. 21
3.2. Экстремумы функции. 21
3.3. Выпуклость и вогнутость функции. Точка перегиба. 23
3.4. Асимптоты.. 24
3.5.Общая схема исследования функции и построение графиков. 25
3.6. Примеры.. 25
3.7. Варианты заданий. 31
3.8. Контрольные вопросы.. 32
Глава 4. Функции нескольких переменных. 32
4.1. Определение функции нескольких переменных. 32
4.2. Частные производные. 33
4.3. Полный дифференциал. 34
4.5. Примеры.. 34
4.6. Варианты заданий. 36
4.7. Контрольные вопросы.. 36
Глава 5. Численное дифференцирование. 36
5.1. Формулы для вычисления первой производной. 37
5.2. Формулы второй производной. 38
5.3. Примеры.. 39
5.4. Варианты заданий. 42
Глава 6 Основы интерполяции. 43
6.1. Постановка задачи. 43
Интерполяционные формулы конечных разностей. 45
6.3. Интерполяционные формулы центральных разностей. 46
6.4. Интерполирование функции с не равноотстоящими узлами. 47
6.5. Варианты заданий. 53
6.6. Контрольные вопросы.. 54
Глава 7. Неопределенный интеграл. 54
7.1. Первообразная функция и неопределенный интеграл. 54
7.2. Основные свойства неопределенного интеграла. 55
7.3. Таблица простейших интегралов. 56
7.4. Основные методы интегрирования. 57
7.4.1. Непосредственное интегрирование. 57
7.4.2. Метод подстановки (замена переменной) 57
7.4.3. Интегрирование по частям.. 58
7.5. Примеры.. 59
7.6. Варианты заданий. 62
7.7. Контрольные вопросы.. 63
Глава 8. Определенный интеграл. 63
8.1. Основные понятия и свойства определенного интеграла. 64
8.2. Основные методы интегрирования. 66
8.2.1. Формула Ньютона-Лейбница. 66
8.2.2. Метод подстановки. 67
8.2.3. Интегрирование по частям.. 68
8.3. Примеры.. 68
8.4. Варианты заданий. 71
8.5. Биологические, физические и медицинские приложения определенного интеграла. 72
Глава 9. Численное интегрирование. 81
9.1. Формула прямоугольников. 81
9.2. Формула трапеций. 82
9.4. Формула Симпсона. 83
9.5. Примеры.. 84
9.6. Варианты заданий. 89
9.7. Контрольные вопросы.. 90
Глава 10. Дифференциальные уравнения. 91
10.1. Основные определения. 91
10.2. Уравнения с разделяющимися переменными. 93
10.3. Однородные уравнения первого порядка. 94
10.4. Линейные уравнения первого порядка. 94
9.5. Примеры.. 96
10.6. Варианты заданий. 103
10.7. Применение дифференциальных уравнений в биологии и медицине. 105
10.8. Варианты заданий. 109
10.9. Контрольные вопросы.. 111
Глава 11. Численные методы решения дифференциальных уравнений. 111
11.1. Метод Эйлера. 112
10.2. Метод Рунге – Кутта. 113
10.3. Примеры.. 114
11.4. Варианты заданий. 117
11.4. Контрольные вопросы.. 119
Глава 12. Элементы теории вероятностей. 119
12.1. Случайное событие. 119
12.2. Комбинаторика. 120
12.3. Вероятность случайного события. 122
Закон сложения вероятностей. 124
12.5. Варианты заданий. 125
12.6. Условная вероятность, закон умножения вероятностей. 129
12.7. Варианты заданий. 133
12.8. Формулы полной вероятности и Байеса. 136
12.9. Варианты заданий. 139
11.10. Формулы Бернулли, Пуассона и Муавра-Лапласа. 144
12.11. Варианты заданий. 151
12.2. Случайные величины.. 155
12.3. Варианты заданий. 164
Глава 13. Статистический анализ результатов исследований. 166
13.1. Основные понятия математической статистики. 166
13.1. Варианты заданий. 171
13.2. Статистические оценки параметров распределения. Выборочные характеристики 172
13.3. Варианты заданий. 175
13.4. Оценка параметров генеральной совокупности по ее выборке. 176
13.5. Варианты заданий. 179
13.6. Интервальная оценка параметров генеральной совокупности. 179
13.7. Варианты заданий. 185
1.8. Контрольные вопросы.. 186
Глава 14. Корреляционный и регрессионный анализ. 186
14.1. Функциональная и корреляционная зависимости. 187
14.2. Коэффициент линейной корреляции и его свойства. 189
14.3. Проверка гипотезы о значимости выборочного коэффициента линейной корреляции 192
14.4. Выборочное уравнение линейной регрессии. Метод наименьших квадратов. 194
14.5. Нелинейная регрессия. 199
14.6. Варианты заданий. 200
Приложение. 203
t-распределение (распределение Стьюдента) 203
Таблица значений функции  ................................. 205
................................. 205
Критические значения выборочного коэффициента корреляции ra. 207
Критерий Колмогорова – Смирнова. 208
Точные и асимптотические границы для верхней грани модуля разности. 208
истинной и эмпирической функции распределения. 208
Распределение Пирсона (х2 – распределение) 209
Распределение Фишера – Снедекора (F-распределение) 213
Библиографический список. 219
 | |
 |
– Конец работы –
Используемые теги: Кафедра, математики, информатики, Практикум0.059
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Кафедра математики и информатики. Практикум
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов