Статистический подход к определению информации.
Любому изучаемому объекту присуща неопределенность его возможных состояний. Чем больше количество состояний, тем выше неопределенность.
Количественная мера беспорядка в системе, выражающаяся в неопределенности его состояний, характеризуется энтропией системы.
Имеется два определения энтропии:
1 определение: энтропия системы равна log числа возможных состояний объекта.
Возможные состояния системы: S = 1,…,S
H0 = log S, (1)
Предположим, для передачи информации мы используем всего два сигнала: 0 и 1.
Последовательность из n двоичных сигналов позволяет описать 2n возможных состоянии.
2n = S 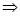 n = log2S
n = log2S
Чаще всего в первом определении в качестве основания log используется 2. в этом случае энтропию системы можно интерпретировать как количество двоичных сигналов (бит), необходимых для передачи сообщения о действительном состоянии системы.
2 определение по Шеннону: первое определение энтропии соответствует так называемой вариационной неопределенности, когда все возможные состояния системы равновероятны. В случае, когда распределение вероятностей системы отличается от равномерного, определение энтропии следует скорректировать.
Формула определения энтропии была предложена Шенноном в 1948 г.
S = 1,…, S
P(S) – вероятность каждого состояния, 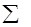 P(S) = 1
P(S) = 1
 (2)
(2)
Покажем, что если все состония системы равновероятны Н=Н0, P(S) = ½
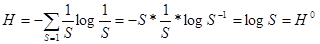
Если состояния системы неравновероятны, то можно показать, что: Н≤Н0.
Наряду с энтропией говорят об информации или неэнтропии, как величине обратной по знаку энтропии: I = -H.
Энтропия обладает свойством аддитивности, т.е. энтропия системы, составленной из 2-х изолированных статистически независимых объектов равна сумме энтропии этих объектов.
Энтропия замкнутой изолированной системы со временем монотонно увеличивается вплоть до достижения максимального значения Н0.
Основоположник теории информации Клод Шеннон исходил из функционального подхода к понятию информации. Он рассматривал ее как снятую неопределенность об объекте в результате получения адресатом некоторого сообщения, касающегося этого объекта.
Пусть изучаемый объект может принять одно из S состояний: х1, х2,…,хS.
Предположим также, что на объект могут поступать воздействия, принимающий одно из М значений: у1, у2,…, уm. Воздействия носят случайный характер.
Введем вектор условных вероятностей P(X(Yj))=(P(X1/Yj), P(X2/Yj),…,P(XS/Yj))
Рассмотрим воздействия на объект Y как сигнал потенциально доступный наблюдению. До приема сигнала известны априорные вероятности Р(Yj) каждого возможного сообщения.
Сообщения, которые получает наблюдатель указывает конкретную реализацию Yj случайные величины Y. Определим информационную ценность полученного сообщения.
До получения сигнала априорные вероятности P0(Xi), i= 1,…,s, состояния объекта можно получить по формуле:
P0(Xi)=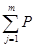 (Xi/Yj)Р(Yj)
(Xi/Yj)Р(Yj)
После получения конкретного сигнала Yj апостериорная вероятность того, что объект будет находиться в этом состоянии задается формулой:
Р/(Xi)=Р(Xi/Yj)
Информационная ценность полученного сигнала равна изменению энтропии объекта в результате получения сигнала, а именно: априорная энтропия объекта:
Н(X)=-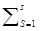 P0(Xs)*logP0(Xs)
P0(Xs)*logP0(Xs)
Апостериорная энтропия объекта после получения сигнала Yj будет равна
Н(X/Yj) = -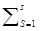 P/(Xs)*logP/(Xs)
P/(Xs)*logP/(Xs)
Количество информации об объекте Х, полученной в результате получения сообщения Yj будет равно:
I(X, Yj)=H(X)-H(X/Yj)
Из последней формулы видно, что различные сигналы несут в себе разное количество информации
.