Детерминированные динамические системы с дискретным временем.
Многие приложения в экономике требуют моделирования систем во времени.
Состояние системы в момент времени t описывается мерным вектором X(t).
X1(t)
X(t) = ….. , X (t) 
Rn ( R – множество всех вещественных чисел)
Xn(t)
t
Эволюция системы со временем описывается функцией
G (X0, t, 
) , где
X0 – начальное состояние системы;
t – время;
- вектор параметров.
Функция g(*) называют также переходной функцией
Функция g(*) – это правило, описывающее текущее состояние как функцию от времени, начальных условий и параметров.
Например: Xt = X0 (1+)t = g (X0, t, )
Функция g(*) как правило не известна. Обычно она задана неявно как решение системы разностных уравнений.
Разностное уравнение или система уравнений – это уравнения в следующей форме : F (t, Xt, Xt+1, …, Xt+m, ) = 0 (1),где
Xt – состояние системы в момент времени t.
Решение уравнения (1) – это последовательность векторов
Xt = 
X0, X1,…, 
Обычно предполагается, что уравнение (1) можно решить аналитически относительно Xt+m и переписать в форме так называемых уравнений – состояний :
Xt+m = f (t, Xt, Xt+1, …,Xt+m-1, ) (2)
Например:
Xt+2 = Xt + Xt+1/2 + t
Любую систему представляют в форме (2) всегда можно ?
Разностное уравнение (2)называется линейным, если F(*) является линейной фуекцией переменных состояний (не обязательно линейно относительно )
В уравнениях (1) и (2) величина m называется порядком системыне является серьезным ограничением, так как системы более высокого порядка путем введения дополнительных переменных и уравнений.
Пример:Xt = f (Xt-1, Yt-1) – система 2-го порядка
Введем Yt = Xt-1
Xt = f(Xt-1, Yt-1)
Yt = Xt-1
Таким образом, мы будем рассматривать только системы 1-го порядка следующего вида:
Xt-1 = f(t, Xt, ) (3)
Уравнение (3) называется автономным, если t не входит в него отдельным аргументом.
Пример:
Рассмотрим динамику основных фондов на предприятии
Kt – стоимость основных фондов предприятия в период t.
- норма амортизации, то есть % основных фондов, которые изъяли на предприятии за год.
It = инвестиции в основные фонды.
Kt+1 = ( 1 - ) Kt + It – уравнение 1-го порядка, линейное, если It = I, тогда
Kt+1 = ( 1 - ) Kt + I – уравнение автономное
Если It = I(t) – неавтономное (зависит от t)
Решение уравнения (3) – это последовательность векторов состояния {Xt}, удовлетворяющих уравнению (3) для всех возможных состояний. Эта последовательность называется траекторией системы. Уравнение (3) показывает, как состояние системы изменяется от периода к периоду, а траектория системы дает ее эволюцию как функцию начальных условий и состояния внешней среды .
Если известно начальное состояние X0, легко получить последовательность решений путем итеративного применения отношения (3), получим переходную функцию следующим образом:
Xt+1 = f (t, Xt, )
{Xt}
X0 = X0
X1 = f ( 0, X0, ) = g (0, X0, )
X2 = f ( 1, X, ) = f (1; f (0, X0, );) = g (1, X0, )
Xt+1 = f (t, Xt, ) = f ( t, g, (t – 1, X0, ),) = g (t, X0, )
Если f (*) однозначная, всюду определенна функция, то существует уникальное решение уравнения (3) для любого X0.
Если функция имеет вид f (t, Xt, ) = / Xt – не всюду опрделенная.
Если f (*) непрерывная дифференциальная функция, то решение также будет гладким относительно и X0
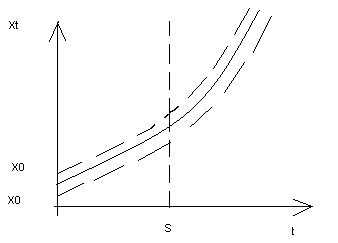
Полученное решение зависит от начального состояния X0.
Задача с граничным условием состоит из уравнения (3) и граничного условия, задаваемого в формуле:
Xs = Xs (4)
Если в уравнении (4) – S = 0 , то оно называется начальным состоянием.
Уравнение (3) имеет много решений, а уравнение (3) + (4) – система – единственное решение, поэтому различают общее и частное решение разностного уравнению (3):
Xtg = X(t, c, ) = {Xt(Xt+1 = f (t, Xt, ))} , где параметр е индексирует частное решение.
Пример:
Xt – размер вклада в момент t
Z - % я ставка
Xt+1 = Xt ( 1+ z ) ; X0 = …
X1 = X0 ( 1 + z)
X2 = X1 ( 1 + z) = X0 ( 1 + z)2 = g (X0, t, z) , где t = 2
Если можно найти общее решение системы (3) . у нас будет полная информация о поведении системы со временем, будет легко определить, как система реагирует на изменение параметров.
К сожалению, общее решение существует только для определенных классов l – го порядка ( в частности для линейных систем )