Автономные системы
Поведение автономных систем задается разностным уравнением
Xt+1 = f (Xt,  ) (1)
) (1)
Автономные системы моделируют ситуации, где структура системы остается неизменной со временем. Это дает возможность использовать для анализа графический метод.
Xt=1 = f (t, Xt,  )
)
 Xt = Xt+1 – Xt = f (t, Xt,
Xt = Xt+1 – Xt = f (t, Xt,  ) - Xt = d (t, Xt,
) - Xt = d (t, Xt,  ) (2)
) (2)
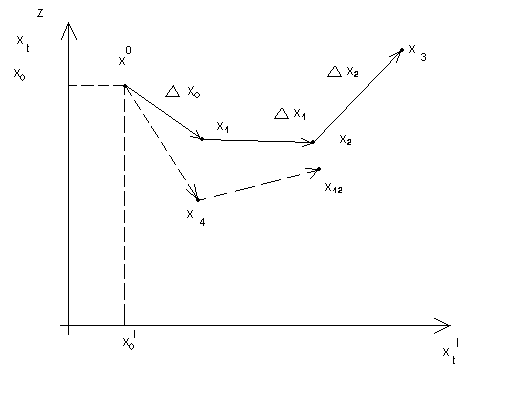
Функция d (*) показывает на сколько изменится состояние системы от периода к периоду. В каждой точке Xt можно сопоставить вектор  Xt в соответствующем уравнении (2) Функция d (*) в этом контексте называется векторным полем
Xt в соответствующем уравнении (2) Функция d (*) в этом контексте называется векторным полем
 X0/t = 0
X0/t = 0
Для автономных систем 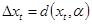 и
и 
В автономных системах все системы, попавшие когда-либо в т. Х0 в последствии следуют одной и той же траекторией. В неавтономных системах поведение зависит также и от того, когда система попала в т. Х0.

При начальном условии Х0 для автономных систем применим уравнение (1):
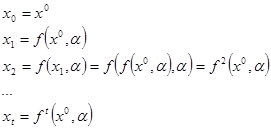
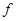 дважды последовательно примененная.
дважды последовательно примененная.
В выше приведенной системе ft означает результат t-кратного итеративного применения функции f ( ) к своему аргументу. Функция ft показывает, куда перейдет система за t периодов из начального состояния.
Пример:
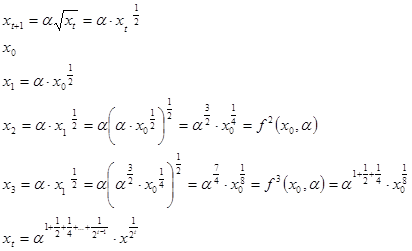
Xt – куда перейдет система из т. Х0 за t периодов времени.
Функция ftиногда называется потоком системы.
Устойчивые состояния. Периодические равновесия. Стабильность.
С течением времени система переходит к устойчивому состоянию. Поэтому нас будет интересовать асимптотическое поведение системы при t → ∞.
Рассмотрим систему 
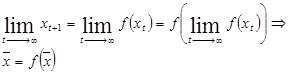
Следовательно, если 
 существует, то
существует, то  .
.
Точка Х, удовлетворяющая уравнению 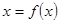 называется неподвижной точкой отображения
называется неподвижной точкой отображения 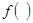 .
.
Точка 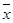 называется в контексте динамических систем устойчивым состоянием или стационарным состоянием.
называется в контексте динамических систем устойчивым состоянием или стационарным состоянием.
Неподвижные точки широко используются для изучения долговременного поведения динамических систем.
Пример:
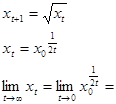
если  , то 1 в противном случае 0
, то 1 в противном случае 0
