Перевод чисел из одной системы счисления в другую
Использование в ЭВМ двоичной системы счисления связано с преодолением дополнительных трудностей, вызванных необходимостью перевода вводимых в ЭВМ чисел в двоичную систему счисления и обратного перевода числовых данных при выводе информации из ЭВМ. Эти преобразования информации в ЭВМ осуществляются автоматически с использованием специально разработанных методов.
Пусть задано число А(q) в q–ичной системе счисления. Требуется найти запись этого числа в р-ичной системе счисления, т.е. В(р).
3.1. Метод непосредственного замещения
Перевод чисел этим методом выполняется следующим образом:
- заданное число А(q) представляется в виде (3.1):
A(q)=an-1´qn-1+…+a0´q0+a –1´q-1+…+a-m´q-m ;
- все цифры ai и основание q в правой части записываются (замещаются) в системе счисления с новым основанием p и выполняются необходимые операции. При этом, если р>q, то изображение цифр в p-ичной системе совпадает с изображением чисел в q-ичной системе. Если же p<q, то необходимо знать представление чисел от p до q в системе счисления с основанием р.
Пример 3.8. Перевести число 357 (8) в десятичную систему счисления.
Решение. 357(8)=3´82+5´81+7´80=192+40+7=239(10).
Пример 3.9. Перевести число 13,5(10) в двоичную систему счисления.
Решение. 13,5(10)=1´101+3´100+5´10-1=1´1010+11+101/1010=1101,1(2) .
3.2. Метод последовательного деления на основание
Этот метод используется для перевода только целых чисел.
Пусть число A(q) требуется записать в р-ичной системе. Допустим, что такое представление получено и новое число В(р) имеет вид:
A(q) = B(p) = bn-1 bn-2 … b1 b0 (p) = bn-1´pn-1 + bn-2´pn-2 + … + b1 p1 + b0.
Разделим число A(q) на р. Так как b0<p, то в результате деления получим целую часть:
A1 = bn-1´pn-2 + bn-2´pn-3 + … + b1
и остаток b0. Отсюда следует, что остаток от деления заданного числа на основаниe р равен значению цифры младшего разряда р-ичного числа. При этом, если p<q, то остаток является цифрой р-ичной системы счисления, а при p>q остаток представляет собой число в q-ичной системе счисления, которое соответствует цифре р-ичной системы (заметим, что деление должно выполняться в q-ичной системе счисления, т.е. в системе, в которой задано исходное число).
Чтобы найти цифру b1 следует отбросить остаток b0, a А1 вновь разделить на р. Получим целую часть
А2 = bn-1´pn-3 + … b3´p + b2
и остаток b1, который равен значению цифры очередного разряда. Последовательное деление продолжается до тех пор, пока не получится частное, меньшее р. Это частное является цифрой старшего разряда искомого р-ичного числа.
Правило перевода. Чтобы перевести целое число из одной системы счисления в другую, необходимо последовательно делить это число и промежуточные частные на основание новой системы счисления, представленное в старой системе. Полученные остатки и последнее частное дадут искомое изображение р-ичного числа, причем первый остаток записывается в младший разряд, а последнее частное – в старший разряд числа.
Пример 3.10. Перевести десятичное число 38 в двоичную систему счисления.
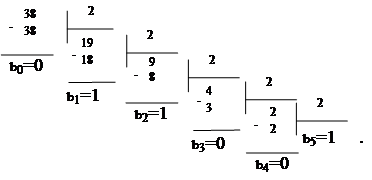Решение:
Ответ: B(2)=b5 b4 b3 b2 b1 b0(2)=100110(2) .
Пример 3.11. Провести обратный перевод числа B(2)=100110(2) в десятичную систему счисления.
Решение: Сначала новое основание системы счисления представим в двоичной системе: 10(10)=1010(2). Далее делим число 100110(2) на основание 1010(2).
100110
1010
10010
1010
Ответ: 100110(2)=b1b0 (10) = 38(10).
3.3. Метод последовательного умножения на основание
Этот метод применяется для перевода из одной системы счисления в другую только правильных дробей.
Пусть правильную дробь A(q) требуется записать в системе счисления с основанием р. Предположим опять, что эта запись найдена
A(q)=B(p)=0, b-1 b-2… b-m(p)=b-1´p-1+b-2´p-2+…+b-m ´p-m.
Если умножить число А на основание новой системы счисления p, то целая часть произведения будет равна b-1, а дробная
A1=b-2´p-1+b-3´p-2 + … + b-m´p-m+1,
причем A1-правильная дробь, т.к. все ai < p.
Таким образом, в результате умножения числа А на основание р получается целая часть, равная значению цифры старшего разряда р-ичного числа. Продолжая умножать дробные части Aj на основание р (целые части при умножении отбрасываются), можно получить остальные цифры искомой дроби: ими являются целые части получаемых произведений. При этом, если p<q, то целые части произведения являются цифрами р-ичной системы счисления, а при p>q целые части представляют собой числа в q-ичной системе счисления, которые необходимо заменить цифрами р-ичной системы.
Правило перевода. Чтобы перевести правильную дробь из одной системы счисления в другую, необходимо последовательно умножать это число и промежуточные произведения на основание новой системы счисления (представленное в старой системе), отбрасывая каждый раз целые части произведений. Эти целые части являются изображением дроби в р-ичной системе.
Пример 3.12. Перевести десятичную дробь A(10)=0,6875(10) в двоичную систему счисления.
Решение. Выполним следующие действия:
Ответ: B(2)=0, b-1 b-2 b-3 b-4=0,1011(2).
Пример 3.13. Провести обратный перевод двоичного числа 0,1011(2) в десятичную дробь.
Решение. В данном примере p>q, поэтому сначала переведем р(10) в двоичную систему счисления: р=10(10)=1010(2). Выполним последовательные умножения:
Ответ: B(10)=0, b-1 b-2 b-3 b-4 = 0,6875.
Следует заметить, что в общем случае дробные числа переводятся из одной системы счисления в другую приближенно, т.е. дробная часть произведения при последовательном умножении на основание может никогда не принимать значение, равное 0. Тогда число разрядов выбирается из условия обеспечения заданной точности.
Для перевода неправильной дроби из одной системы счисления в другую необходим раздельный перевод целой и дробной частей по правилам, описанным выше. Полученные результаты записывают в виде новой дроби.
3.4. Перевод чисел из восьмеричной системы счисления
в двоичную и наоборот
Существует особый случай перевода, если основание одной системы счисления является целой степенью основания другой системы. В этом случае перевод чисел существенно упрощается. В ЭВМ наиболее часто используется переход между 8-ричной и 2-ичной системами. Поэтому ограничимся рассмотрением только этого случая.
Пусть задано число А в 8-ричной системе:
A=an-1 an-2…a1 a0(8) = an-1´8n-1+an-2´8n-2+…+a1´81+a0´80.
Пусть число А записано в 2-ичной системе счисления:
A=bl-1 bl-2…b2 b1 b0 (2) = bl-1´2l-1+bl-2´2l-2+…+b2´22+b1´21+b0.
Так как числа одинаковые, мы можем приравнять их друг другу:
an-18n-1+an-28n-2+…+a181+a080= bl-1 2l-1+2l-2 2l-2+…+b2 22+b1 21+b0 20 .
Если разделить обе части равенства на 8, то получим одинаковые частные
an-1 8n-2 + an-2 8n-3 +…+ a1 = bl-1 2l-4 + bl-2l-5 +…+ b4 21 + b3
и одинаковые остатки:
a0(8)=b2 22 + b1 21 + b0 20 = b2 b1 b0 (2).
Следовательно, младшая восьмеричная цифра a0(8) выражается трехразрядным двоичным числом b2 b1 b0 (2).
Если частное вновь разделить на 8, то получим
а1(8)=b5 b4 b3 (2).
Аналогично можно получить все остальные разряды.
Правило перевода. Для перевода восьмеричного числа в двоичную систему счисления достаточно каждую восьмеричную цифру заменить равным ей трехразрядным двоичным числом (двоичной триадой).
Пример 3.14. Перевести восьмеричное число 571,034 (8) в двоичное.
Решение.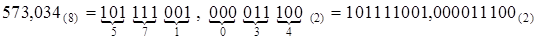 
.
Для перевода числа из двоичной системы в восьмеричную достаточно разбить его вправо и влево от запятой на триады и заменить каждую триаду соответствующей ей восьмеричной цифрой. Если крайние триады окажутся неполными, их следует дополнить нулями.
Пример 3.15. Перевести двоичное число 11011111011001 , 1001(2) в восьмеричное.
Решение.
.
Простота перехода от восьмеричной системы к двоичной иногда используется для перевода чисел из десятичной системы счисления в двоичную: сначала от десятичной системы переходят к восьмеричной, а затем уже к двоичной.