Выборочные распределения на шкале Nom
Напомним, что случайная величина X, принимающая одно из n допустимых значений A, B, C и т.д. имеет номинальную шкалу тогда, когда для любой пары этих значений применимы только понятия “равно” или “неравно”.
Для подобных СВ не существует понятий математического ожидания, как и других моментов распределения. Но понятие закона распределения имеет смысл – это ряд вероятностей PA = P(X=A) для каждого из допустимых значений. Соответственно, итоги наблюдения над такой СВ дадут нам частоты fA. Если у нас имеется всего N наблюдений за такой величиной, то иногда имеется возможность выдвинуть и проверить гипотезы о природе такой случайной величины, ее законе распределения и параметрах этого закона. Ситуации, когда это возможно сделать, не так уж и редки – всё зависит от понимания нами природы, сути случайных событий, от многозначности случайной величины и, конечно же, от количества наблюдений.
6.15.1 Случай двухзначной случайной величины, N<50
Пусть нам крайне важно оценить "симметричность" некоторой случайной величины на номинальной двухпозиционной шкале со значениями "+" и "–" по наблюдениям за этой величиной. Если таких наблюдений было N+ =15 и N– = 25 соответственно, то это вся информация, которая у нас есть. Что же можно узнать из нее? Оказывается – достаточно много и иногда … даже надёжно!
В конце концов, мы можем полагать вероятность значения "+" на данной номинальной шкале равной p и тогда q = (1 – p) даст нам вероятность положения "–" на этой же шкале. Таким образом, мы уже построили закон распределения и дело остается за оценкой его единственного параметра p.
По сути дела у нас есть одна дискретная случайная величина – число появлений X на "первой" позиции своей номинальной шкалы и это число составляет S= N+ .
Но совершенно ясно, что новая случайная величина S имеет биномиальный закон распределения и вероятность наблюдения N+ =15 вполне можно вычислить, если знать или задаться значением p.
Выдвинем вначале нулевую гипотезу о симметрии распределения X и альтернативную ненаправленную гипотезу –
Њ0: p=q= 0.5; Њ1: p#q# 0.5.
Как обычно, оценим вероятность имеющегося наблюдения при верной нулевой гипотезе. Используя формулы расчета вероятности P(S£15) или специальные таблицы биномиального распределения находим для 5%–го уровня значимости, что критическое значение S составляет 27, т.е. заметно больше наблюдаемого N+ =15. Следовательно, наши наблюдения статистически значимы – можно отвергнуть гипотезу Њ0, рискуя при этом ошибиться только в пяти случаях из 100.
Рассмотрим теперь несколько иной пример. Пусть нам необходимо проверить партию изделий в 50 штук при следующем правиле – вся партия бракуется, если доля бракованных изделий превышает 10%.
Выдвигаем гипотезы
Њ0: p £ 0.10 и q ³ 0.90; Њ1: q £ 0.90 и p ³ 0.10.
Можно сразу решить вопрос о количестве проверок N, достаточном для обоснованном решении об отбрасывании нулевой гипотезы. Поскольку мы имеем биномиальное распределение числа бракованных изделий в выборке из N наблюдений, то нам надо, прежде всего, установить порог значимости наблюдений – примем его традиционно, равным 0.05.
Теперь можно начинать наблюдения, накапливая результаты и по мере роста числа наблюдений контролировать их значимость. Покажем, как это делать в ситуации, когда N=48, а число бракованных изделий к этому времени составило 4.
По сути дела, нам надо вычислить вероятность появления 4 отрицательных исходов и всех еще менее вероятных в серии из 48 испытаний. Правда сделать это вручную слишком сложно – придется работать с биномом 48 степени. Поэтому при отсутствии компьютерной программы можно использовать специальные таблицы биномиального распределения.
В них можно найти значение числа событий с вероятностью 0.10 каждое, достаточное для отбрасывании нулевой гипотезы с вероятностью ошибки первого рода в 5%. В наших условиях это число равно 9, значит при наблюдаемом меньшем числе бракованных изделий (всего 4) гипотезу Њ0 следует принять и всю партию не браковать.
6.21.1 Случай двухзначной случайной величины, N>50
При достаточно больших выборках можно поступать и иначе. В качестве правила проверки гипотез используют так называемый критерий "хи–квадрат”
c2 = å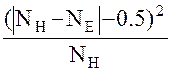 . {6–1}
. {6–1}
Эта непрерывная случайная величина была предложена видным статистиком Р.Фишером для проверки гипотез о соответствии выборочного распределения некоторому заданному закону. Для этого используются экспериментальные частости NE и вычисленные в соответствии Њ0 “теоретические” NH . Разумеется, суммирование ведется по всем допустимым значениям СВ. В нашем примере у нее всего лишь два значения (изделие годно или бракованное), поэтому в числителе надо иметь т.н. поправку на непрерывность. Она корректирует влияние природы распределений: дискретное у наблюдаемой величины и непрерывное у критерия Фишера.
Изменим условия предыдущего примера – пусть N= 100, число бракованных изделий составило NE–=12. Нетрудно определить NE+=88, но что касается "гипотетических" частостей NH– и NH+, то эти величины зависят от того, как мы сформулируем гипотезы. Если их оставить без изменения, то эти частости составят NH+ = 90 и NH– = 10. Вычисление выборочного значения c2–критерия не вызывает проблем, важнее знать – как использовать результат расчета. В нашем примере расчетное значение критерия составит 0.25. Кроме конкретного значения критерия надо учесть так называемое число степеней свободы. В нашем случае это 1, а в общем случае надо уменьшить число допустимых значений n на единицу. Ну, а далее требуется взять стандартные статистические таблицы, учесть пороговое значение ошибки первого рода – и получить ответ. Для примера приведем часть такой таблицы при a=0.05
Таблица 6–1
| Степеней свободы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Критическое c2 | 3.84 | 5.99 | 7.82 | 9.49 | 11.1 | 12.6 | 14.1 | 15.5 | 16.9 |
Если наблюдаемое значение c2 меньше критического, гипотеза Њ0 может быть принята.
В условиях нашего примера расчетное значение критерия c2 составляет всего лишь 0.25, что меньше критического 3.48 (для одной степени свободы) и отвергать гипотезу Њ0 (браковать всю партию) нет оснований. Но, если бы мы наблюдали не 12, а 17 случаев брака, то расчетное значение критерия составило бы около 4.62 и гипотезу Њ0 пришлось бы отвергнуть.