I §2. Предполные классы

Здесь мы рассмотрим 5 замкнутых классов, играющих особую роль в вопросе о функциональной полноте Они называются предполными. причина будет выявлена ниже.

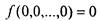1) Класс - класс функций, сохраняющих 0, т.е. функций, для которых. Замкнутость класса 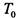очевидна: если в

функцию вместо некоторых переменных

подставить функции, принадлежащие , то на нулевом наборе

аргументов все они имеют значение 0, и для внешней функциинабор ее переменных будет также нулевым, откуда Z = 0.

2) Класс 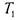- класс функций, сохраняющих 1, те функций, для

которыхЗамкнутость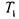устанавливается аналогично

предыдущему.

Примерами функций, принадлежащих классам 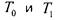, служат

функции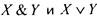, отрицаниене принадлежит ни

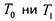
функция принадлежит, но не принадлежитимпликация

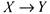напротив, не принадлежит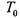, но принадлежит

3) Для определения следующего класса введем понятие двойственности. Двойственная функциядля функции

- функция . Если на

наборе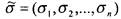функция 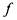принимает значение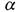, то

двойственная ей функция 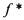на противоположном

ч

наборе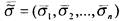принимает противоположное значение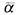

Упражнение.Проверьте, например, что двойственной функцией к

конъюнкции 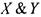является дизъюнкция , константа 1

двойственна константе 0.

Для булевых функций справедлив принцип двойственности -

если в формуле F , представляющей функцию, все знаки функций заменить соответственно на знаки двойственных функций, то полученная формула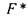будет представлять функцию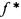, двойственную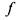

Класс S самодвойственных функций- то есть функций таких, что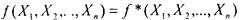. Из определения следует, что

двоичный набор значений самодвойственной функции антисимметричен относительно своей середины. Таким способом удобно проверять по таблице самодвойственность функции. Например, можно убедиться, что

одноместные функции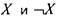- самодвойственные, а среди функций

двух переменных самодвойственными являются только функции с одной

несущественной переменной. Функция большинства 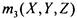(см

§1 гл.З) является самодвойственной

Из определения нетрудно вывести, что класс самодвойственных функций - замкнутый, поскольку в любой суперпозиции на противоположных наборах внутренние подформулы принимают противоположные значения, и, тем самым, наборы значений аргументов

внешней функции также противоположны. Пусть

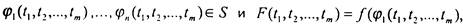
i - суперпозиция этих самодвойственных функций. Тогда [поскольку

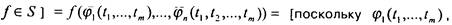
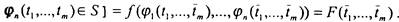
^!' 4) В начале §1 гл.4 мы убедились в возможности представления любой функции многочленом Жегалкина.

Подмножеством множества многочленов является класс L 'линейных функций- функции вида 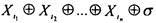. Здесь

- переменные, 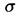- булева константа (0 или 1).

Очевидно, что класс линейных функций - замкнутый: подстановка сумм вместо переменных представляет собой сумму; при этом некоторые пары слагаемых могут взаимно сократиться ввиду эквивалентности

Пример:Пусть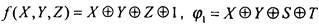

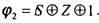Тогда суперпозиция [в

функцию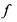подставляем функциювместо X и функцию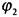вместо Y ] представляет собой линейную функцию:

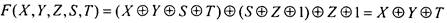
5) Введем отношение частичного порядка для булевых векторов:

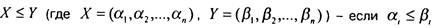для

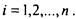Заметим, что для булевых переменных строгое неравенство 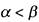означает, чтопоскольку других возможностей нет.

Равенство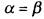добавляет варианты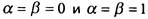. Поэтому

аргументов все они имеют значение 0, и для внешней функциинабор ее переменных будет также нулевым, откуда Z = 0.

2) Класс 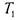- класс функций, сохраняющих 1, те функций, для

которыхЗамкнутость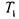устанавливается аналогично

предыдущему.

Примерами функций, принадлежащих классам , служат

функции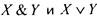, отрицание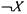не принадлежит ни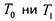

функция 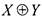принадлежит, но не принадлежитимпликация

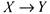напротив, не принадлежит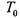, но принадлежит

3) Для определения следующего класса введем понятие двойственности. Двойственная функциядля функции

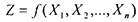- функция . Если на

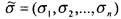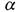наборефункция принимает значение, то

двойственная ей функция 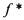на противоположном

ч

наборе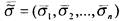принимает противоположное значение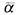

Упражнение.Проверьте, например, что двойственной функцией к

конъюнкции 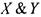является дизъюнкция , константа 1

двойственна константе 0.

Для булевых функций справедлив принцип двойственности -

если в формуле F , представляющей функцию, все знаки функций заменить соответственно на знаки двойственных функций, то полученная формула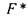будет представлять функцию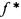, двойственную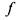

Класс S самодвойственных функций- то есть функций таких, что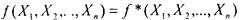. Из определения следует, что

двоичный набор значений самодвойственной функции антисимметричен относительно своей середины. Таким способом удобно проверять по таблице самодвойственность функции. Например, можно убедиться, что

одноместные функции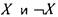- самодвойственные, а среди функций

двух переменных самодвойственными являются только функции с одной

несущественной переменной. Функция большинства 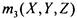(см

§1 гл.З) является самодвойственной

Из определения нетрудно вывести, что класс самодвойственных функций - замкнутый, поскольку в любой суперпозиции на противоположных наборах внутренние подформулы принимают противоположные значения, и, тем самым, наборы значений аргументов

внешней функции также противоположны. Пусть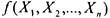

i - суперпозиция этих самодвойственных функций. Тогда [поскольку

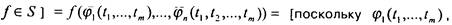
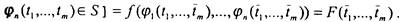
^!' 4) В начале §1 гл.4 мы убедились в возможности представления любой функции многочленом Жегалкина.

Подмножеством множества многочленов является класс L 'линейных функций- функции вида 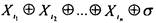. Здесь

- переменные, 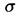- булева константа (0 или 1).

Очевидно, что класс линейных функций - замкнутый: подстановка сумм вместо переменных представляет собой сумму; при этом некоторые пары слагаемых могут взаимно сократиться ввиду эквивалентности

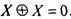
Пример:Пусть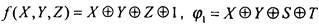

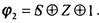Тогда суперпозиция 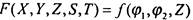[в

функцию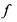подставляем функциювместо X и функцию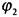вместо Y ] представляет собой линейную функцию:

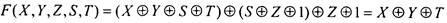
5) Введем отношение частичного порядка для булевых векторов:

для

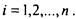Заметим, что для булевых переменных строгое неравенство 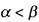означает, что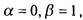поскольку других возможностей нет.

Равенство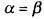добавляет варианты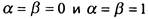. Поэтому

неравенствуудовлетворяют 3 пары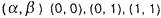и не

удовлетворяет только пара (1, 0) Можно заметить, что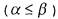эквивалентно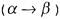

Класс М монотонных функций- это класс функций таких, что если , то , т е. функция на большем наборе

принимает не меньшее значение.

Среди заданных в табл 6 функций двух существенных переменных монотонными являются конъюнкция и дизъюнкция.

Покажем, что класс монотонных функций - замкнутый Пусть функции

что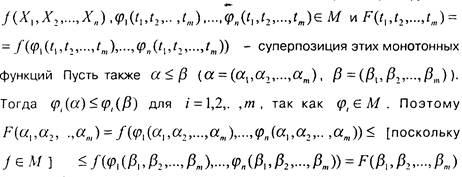и требовалось доказать.

Отметим, что для каждой упорядоченной пары (А, В) различных

классов из пяти рассмотренных предполных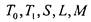существует

функция, входящая в А и не входящая в В . Таблица 8 содержит такие примеры каждая функция таблицы входит в класс, соответствующий строке и не входит в класс, соответствующий столбцу Например, входит

в Л/ , но не входит в S функция-константа 0; входит в S, но не входит в L функция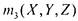Из этого замечания можно сделать важный

вывод никакой из пяти классов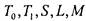не входит целиком ни в

какой из остальных четырех