Теоретические сведения.
Классификация задач.
Линейное уравнение второго порядка в частных производных в общем случае имеет вид:
 (1*)
(1*)
где a, b, c, d, e, g, f - известные функции от x и y. Если a, b, c, d, e, g – константы, то (1*) называется уравнением с постоянными коэффициентами. Если f(x, y)=0, то уравнение является однородным.
Уравнение (1) называется эллиптическим, если D < 0; гиперболическим,
если D > 0; параболическим, если D = 0. D - дискриминант квадратичной формы:
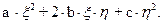

При помощи невырожденного преобразования U(x, y) 
уравнение (1) можно привести к одному из следующих канонических видов:
 - эллиптический
- эллиптический
 - гиперболический
- гиперболический
 - параболический
- параболический
Постановка задач. При математическом описании физического процесса надо, прежде всего, поставить задачу, т. е. сформулировать условия, достаточные для однозначного определения процесса. Дифференциальные уравнения имеют бесчисленное множество решений, поэтому для однозначного определения процесса необходимы также дополнительные условия - краевые и начальные. Краевые и начальные условия зависят от типа уравнения. Задача, в которой поставлены краевые и начальные условия называется смешанной задачей.
Краевые задачи для уравнения Пуассона.
Исследование стационарных процессов различной физической природы часто приводит к необходимости решать уравнения эллиптического типа. Простейшим и наиболее распространённым уравнением этого типа является уравнение Пуассона:

Однородное уравнение Пуассона (при 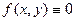 ) называется уравнением Лапласа. Такими уравнениями описываются явления электростатики или магнитостатики. В частности, потенциал
) называется уравнением Лапласа. Такими уравнениями описываются явления электростатики или магнитостатики. В частности, потенциал  электрического поля, образованного системой электродов и объёмным зарядом частиц с плотностью
электрического поля, образованного системой электродов и объёмным зарядом частиц с плотностью 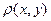 , удовлетворяет всюду внутри области, не занятой электродами, уравнению:
, удовлетворяет всюду внутри области, не занятой электродами, уравнению:
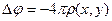 ,
, 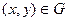 (1)
(1)
при условии, что на границе области (на электродах) поддерживаются заданные значения потенциала:
 ,
, 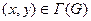 , (2)
, (2)
где 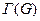 - граница области G,
- граница области G,  - функция, определённая на всех точках границы.
- функция, определённая на всех точках границы.
Уравнения (1) и (2) называют первой краевой задачей для уравнения Пуассона.
Подобной же постановке удовлетворяет задача стационарного двумерного распределения температуры в пластине конечной толщины, если внутри пластины распределены по заданному закону источники (стоки) тепла, описываемые функцией 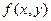 , а на границах пластины поддерживается заданная температура.
, а на границах пластины поддерживается заданная температура.
Возможны и другие постановки краевых задач для уравнения Пуассона. Например:
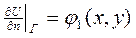 ,
, 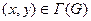 ,
,
где 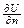 - производная по нормали к граничной кривой в точке
- производная по нормали к граничной кривой в точке  границы Г. Это есть вторая краевая задача, или задача Неймана.
границы Г. Это есть вторая краевая задача, или задача Неймана.
Метод сеток.
Метод сеток состоит в сведении решения краевой задачи к решению алгебраических уравнений для так называемой сеточной функции. Для этого область G непрерывного изменения аргумента заменяется областью дискретного его изменения. Дифференциальный оператор заменяется некоторым разностным оператором. Краевые и начальные условия заменяются на соответствующие разностные аналоги. Выберем в области, где ищется решение дифференциального уравнения, некоторое конечное множество точек, в которых и будем искать решение уравнения. Ясно, что чем больше мы возьмем таких точек, тем точнее решим уравнение. Множество таких точек называется сеткой, отдельные точки – узлы сетки. Функция, определенная в узлах сетки, называется сеточной функцией.
Пусть ωh – сетка в некоторой области G, Hh – линейное пространство сеточных функций, заданных на ωh ; H0 –линейное пространство гладких функций 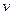 (x) ;
(x) ;  - норма в H0 ;
- норма в H0 ;  - норма в Hh. Предполагается, что:
- норма в Hh. Предполагается, что:
1) существует оператор проектирования Ph такой, что
Ph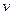 =
=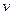 h
h Hh для любого
Hh для любого  H0
H0
2) нормы  и
и  согласованы, т. е.
согласованы, т. е.  ||Ph
||Ph 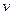 || =
|| = 
Рассмотрим некоторый дифференциальный оператор λ, заданный в H0, и оператор λh, преобразующий сеточную функцию 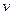 h в сеточную функцию λh
h в сеточную функцию λh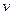 h, заданную на ωh.
h, заданную на ωh.
Погрешностью аппроксимации оператора λ разностным оператором λh называется сеточная функция ψh = λh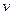 h – (λ
h – (λ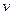 )h, в сеточном пространстве Hh , где
)h, в сеточном пространстве Hh , где 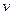 h= Ph
h= Ph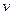 , (λ
, (λ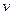 )h= Ph(λ
)h= Ph(λ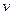 ),
), 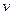 - любая функция из H0. Если при этом
- любая функция из H0. Если при этом
|| ψh ||h= ||λh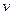 h - (λ
h - (λ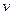 )h||h = O(hm), то разностный оператор λh аппроксимирует дифференциальный оператор λ с порядком m>0.
)h||h = O(hm), то разностный оператор λh аппроксимирует дифференциальный оператор λ с порядком m>0.
При формулировке соответствующей разностной задачи необходимо аппроксимировать не только дифференциальное уравнение, но и краевые и начальные условия.
Разностная аппроксимация простейших дифференциальных операторов.
Пусть дан линейный дифференциальный оператор L, действующий на функцию v=v(x). Заменяя входящие в Lv производные разностными отношениями, получим вместо Lv разностное выражение Lhvh, являющееся линейными комбинациями значений сеточной функции vh на некотором множестве узлов сетки, называемом шаблоном. Такая приближенная замена Lv на Lhvh называется аппроксимацией дифференциального оператора разностным оператором ( или разностной аппроксимацией оператора L).
Изучение разностных аппроксимаций оператора L вначале производят локально, т.е. в любой фиксированной точке x области wh. Прежде чем приступать к разностной аппроксимации оператора необходимо выбрать шаблон, т.е. указать множество соседних с узлом хi узлов, в которых значения сеточной функции vh(xi)=v(xi) могут быть использованы для аппроксимации оператора L.
Обозначим: y(x)=Lhv(x)-Lv(x) при h®0. Величина y(x) называется погрешностью разностной аппроксимации Lv в точке х.
Говорят, что Lh аппроксимирует дифференциальный оператор L с порядком m>0 в точке х, если
y(x)=Lhv(x)-Lv(x)=О(hm).