Решение задачи.
Задание: получить приблизительное решение данной краевой задачи уравнения в частных производных математической физики методом сеток.
 (1)
(1)
Классификация задачи.
Данное уравнение является уравнением эллиптического типа. Его можно интерпретировать как описание распределения температуры в пластине конечной толщины, на всех краях которой поддерживается постоянная во времени нулевая температура.
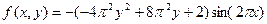 - функция, описывающая распределение внутри пластины источников (стоков) тепла.
- функция, описывающая распределение внутри пластины источников (стоков) тепла.
Применение метода сеток при решении уравнения Пуассона.
Аппроксимируем данное уравнение, используя пятиточечный шаблон "крест".
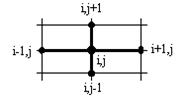 Аппроксимация дифференциального оператора
Аппроксимация дифференциального оператора 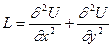 на этом шаблоне имеет вид:
на этом шаблоне имеет вид:
 ,
,
где 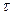 - шаг сетки по j , h - шаг сетки по i, или
- шаг сетки по j , h - шаг сетки по i, или 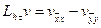 .
.
Погрешность данной аппроксимации 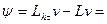
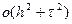 .
.
Если известна искомая функция U(x,y) в точках:
(i-1,j) ; (i+1,j) ; (i,j+1) ; (i,j-1),
то значение U(x,y) в точке (i,j) может быть приближенно найдено следующим образом:
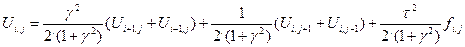 где
где 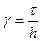 . (2)
. (2)
Это уравнение должно выполняться для всех внутренних узлов сетки, т.е. для  . Для того, чтобы система стала полностью определенной надо дополнить ее уравнениями, полученными при аппроксимации начальных и граничных условий. В нашем случае, начальные условия аппроксимируются следующим образом:
. Для того, чтобы система стала полностью определенной надо дополнить ее уравнениями, полученными при аппроксимации начальных и граничных условий. В нашем случае, начальные условия аппроксимируются следующим образом:
U0,j = Ui,0 = UM,j = Ui,N =0 i=0..M, j=0..N. (3)
Система уравнений (2) и (3) является полностью определённой линейной системой алгебраических уравнений для 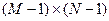 неизвестных значений сеточной функции Ui,j (i=1,2,…,M-1; j=1,2,…N-1). Порядок аппроксимации данной разностной схемы
неизвестных значений сеточной функции Ui,j (i=1,2,…,M-1; j=1,2,…N-1). Порядок аппроксимации данной разностной схемы 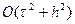 .
.
Метод верхней релаксации.
Для решения данной системы воспользуемся методом верхней релаксации, который является обобщением метода Зайделя и вырождается в него при параметре сходимости 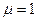 .
.
Применительно к нашей конечно-разностной схеме, метод верхней релаксации записывается в виде:
 (4)
(4)
В итерационной процедуре (4) сначала на (k+1)-ой итерации находится промежуточное значение 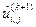 по уже известным на данном шаге значениям сеточной функции
по уже известным на данном шаге значениям сеточной функции 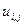 с помощью первой формулы, а затем окончательное значение
с помощью первой формулы, а затем окончательное значение  находится по второй формуле.
находится по второй формуле.
Процесс (4) сходиться для всех значений 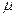 , удовлетворяющих неравенству
, удовлетворяющих неравенству 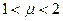 . Вопрос о выборе оптимального значения
. Вопрос о выборе оптимального значения 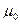 из этого промежутка является достаточно сложным в теоретическом отношении, но в результате машинного эксперимента можно получить значения, близкие к оптимальному. Программа epsilon, написанная в среде MatLab изучает скорость сходимости итерационной процедуры в зависимости от параметра сходимости. В основе лежит решение данного уравнения на сетке фиксированного размера за фиксированное число шагов (например, на сетке размерностью
из этого промежутка является достаточно сложным в теоретическом отношении, но в результате машинного эксперимента можно получить значения, близкие к оптимальному. Программа epsilon, написанная в среде MatLab изучает скорость сходимости итерационной процедуры в зависимости от параметра сходимости. В основе лежит решение данного уравнения на сетке фиксированного размера за фиксированное число шагов (например, на сетке размерностью 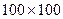 за 100 шагов). Результатом выполнения данной программы является погрешность, достигнутая на последнем итерационном шаге. Используя эту функцию можно получить значение параметра
за 100 шагов). Результатом выполнения данной программы является погрешность, достигнутая на последнем итерационном шаге. Используя эту функцию можно получить значение параметра 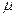 , близкое к оптимальному. Для этого написана функция definition, с помощью которой было получено
, близкое к оптимальному. Для этого написана функция definition, с помощью которой было получено 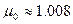 . Это значение использовалось при конечных вычислениях в программе main.
. Это значение использовалось при конечных вычислениях в программе main.
Модельная задача.
Для проверки сходимости метода верхней релаксации была рассмотрена следующая модельная задача:
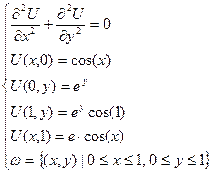
решением которой является функция 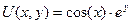 . Результаты выполнения соответствующей программы model приведены в Приложении. Также была рассмотрена зависимость ошибки численного решения данной системы от числа разбиений сетки.
. Результаты выполнения соответствующей программы model приведены в Приложении. Также была рассмотрена зависимость ошибки численного решения данной системы от числа разбиений сетки.
Метод матричной прогонки
Умножим все уравнения системы (2) на 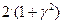 и перенесём все неизвестные в левую часть. Учитывая граничные условия (3), получим систему следующего вида:
и перенесём все неизвестные в левую часть. Учитывая граничные условия (3), получим систему следующего вида:
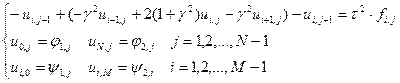
Введём векторные обозначения:
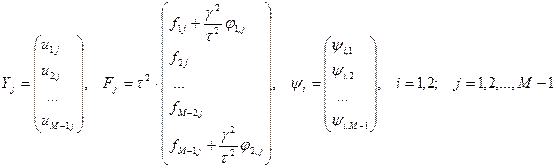
где 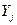 - j-я вектор строка матрицы неизвестных ((u));
- j-я вектор строка матрицы неизвестных ((u)); 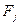 - j-й вектор правых частей с добавками в первой и последней компонентах.
- j-й вектор правых частей с добавками в первой и последней компонентах. 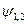 - сеточные векторы граничных условийсоответсвтенно на нижней и верхней сторонах прямоугольника. В этих обозначения система запишется в следующем векторно-матричном виде:
- сеточные векторы граничных условийсоответсвтенно на нижней и верхней сторонах прямоугольника. В этих обозначения система запишется в следующем векторно-матричном виде:
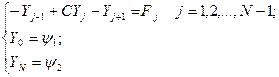
Матрица С размерностью (M-1)x(N-1) имеет следующий трёхдиагональный вид:
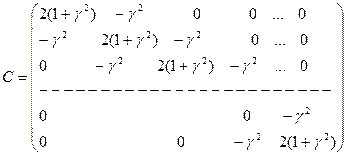 (5)
(5)
Полученную систему можно решать методом матричной прогонки, являющимся формальным обобщением метода обычной(скалярной) прогонки. При этом роль прогоночных коэффицентов 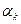 будут играть матрицы
будут играть матрицы 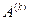 , а роль коэффицентов
, а роль коэффицентов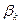 - векторы
- векторы  . Соответствующие формулы прогонки преобретают вид:
. Соответствующие формулы прогонки преобретают вид:

Где 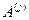 и С – матрицы порядка (M-1)x(N-1);
и С – матрицы порядка (M-1)x(N-1); 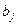 и
и 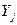 - векторы размерности M-1.
- векторы размерности M-1.
Достаточное условие устойчивости матричной прогонки для данной системы имеет вид 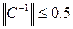 и автоматически выполняется для трёхдиагональной матрицы С вида (5).
и автоматически выполняется для трёхдиагональной матрицы С вида (5).