Численные методы решения разностных уравнений математической физики

Московский Государственный Институт Электронной Техники

( Технический Университет )

Курсовая работа по теме :

Численные методы решения разностных уравнений математической физики

 

Вариант №4.

 

Выполнил: Воронин А.Ю.

Группа: МП-33

Руководитель: Соколова Т.В.

 

МОСКВА 1999 г.

Постановка задачи.

 

Задание: получить приблизительное решение данной краевой задачи уравнения в частных производных математической

физики методом сеток.

 

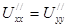
Данное уравнение является уравнением гиперболического типа и физически отражает процесс колебания струны. Искомое решение U(x,y) - вертикальное отклонение струны в точке x в момент времени t.

Данная краевая задача состоит в нахождении функции U(x,y), удовлетворяющей уравнению, а также заданным начальным и граничным условиям.

Граничное условие рода определяет закон движения правого конца струны так называемое условие «упругого закрепления».Для левого конца в качестве граничного условия задано условие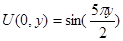

Начальные условия и 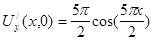задают начальную форму струны и распределение скоростей в начальный момент времени.

 

 

РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ ЯВНОЙ РАЗНОСТНОЙ СХЕМЫ

В явной разностной схеме значение сеточной функции на последующем слое полностью определяется значением её на предыдущем слое по рекуррентным формулам. В данной задаче аппроксимацию дифференциальных операторов проведём по следующим шаблонам

2.1 Аппроксимация дифференциального уравнения

Для сведения задачи к явной разностной схеме используем шаблон " крест".

Получаем конечно-разностную систему :

Обозначим 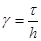и выразим через остальные значения сеточной функции,

входящие в уравнение:

i = 1,.....,m-1;

j = 1,.....,n-1.

 

Уравнение (1) должно выполняться для всех внутренних узлов сетки . Для того чтобы система стала полностью определенной , необходимо дополнить ее уравнениями получаемыми из аппроксимации краевых и начальных условий.

 

2.2 Аппроксимация 1-го начального условия.

2.3 Аппроксимация 1-го граничного условия.

Аппроксимация краевого условия второго рода используется только для нахождения решения на границе i=0 в явном виде:

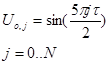(3)

2.4 Аппроксимация 2-го начального условия.

Для более точного аппроксимирования 2-го начального условия разложим 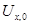в окрестности точки 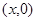по формуле Тейлора и используя начальные условия перейдем к конечным разностям:

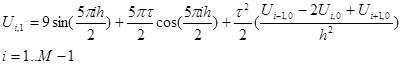(4)

Формула (4)используется на начальном этапе для вычисления значения функции U на первом слое, по известным значениям функции на нулевом слое и на границе .

 

2.5 Аппроксимация 2-го граничного условия.

Для более точного аппроксимирования 2-го граничного условия разложим в окрестности точки (1,y ) по формуле Тейлора:

Используя уравнение краевой задачи и второе граничное условие получаем:

Перейдя к конечным разностям, записываемыми в узле 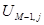, получаем:

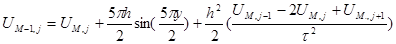(5)

Выражая из него получаем:

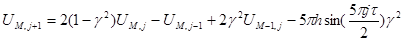(6)

Найдем необходимую точку. Из (4) , при

Откуда -

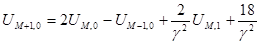(7)

Из (5) , при :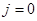

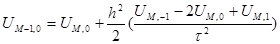
Откуда -

(8)

Из (1) , при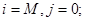

(9)

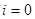Итак прииопределены. Включается рекуррентная процедура.

Порядок аппроксимации данной разностной схемы .

 

Устойчивость решения.

Для уравнений гиперболического типа метод спектральных гармоник

приводит к следующему условию устойчивости:

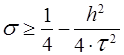(7),

т.е. если это условие устойчивости не будет выполнено, то в процессе рекуррентного решения возможно накапливание ошибок от слоя к слою.

Отсюда, в частности, получаем для явной схемы () условие устойчивости Куранта-Леви: .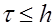

 

РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ НЕЯВНОЙ РАЗНОСТНОЙ СХЕМЫ.

Рассмотрим снова краевую задачу . Для аппроксимации уравнения используем Т-образный пятиточечный шаблон . Уравнение аппроксимируется следующими уравнениями :

 

3.1 Аппроксимация дифференциального уравнения

 

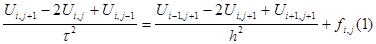
Обозначим 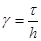и запишем (1) к виду удобному для применения метода прогонки:

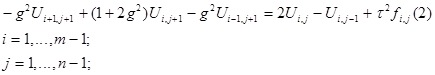
3.2 Аппроксимация 1-го начального условия

(3)

3.3 Аппроксимация 1-го граничного условия

(4)

 

3.4 Аппроксимация 2-го начального условия

Для более точного аппроксимирования 2-го начального условия разложим 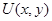в окрестности точки 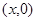по формуле Тейлора и используя 1-ое и 2-ое начальное условия перейдем к конечным разностям:

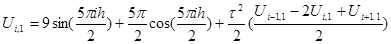(5)

Эта формула отличается от аналогичной для явной схемы тем, что аппроксимация разностной производной второго порядка по 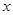производится на первом слое, а не на нулевом. Запишем (5) к виду удобному для применения метода прогонки:

(6)

3.5 Аппроксимация 2-го граничного условия.

При

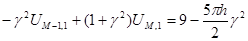(7)

При

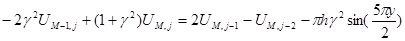
3.6 Вычисления прогоночных коэффициентов

 

Сначала найдем на слое . Определим прогоночные коэффициенты.

Учитывая 1-ое граничное условие и уравнение (6) получаем:

a_i = b_i =

C_i = 1 +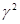

f_i =

b₀ = 0, C₀ = 1, f₀ =

Теперь вычислим граничные прогоночные коэффициенты

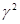a_M = , C_M = 1+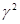, f_M =.

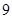Методом прогонки находим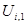где ;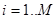

Теперь зная значения находим где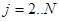

Используя уравнение (2) находим прогоночные коэффициенты:

a_i = b_i =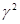

C_i = 1 +

f_i = 2U_i,j - U_i,j-1

b₀ = 0, C₀ = 1, f₀ = .

Теперь вычислим граничные прогоночные коэффициенты

a_M = , C_M = 1+, f_M =.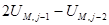

Методом прогонки находим где;

Тексты программ.

 

Явная схема.

 

clear

%----------------Число разбиений по осям-------------

M=50; N=55;

%------------------Вычисление шага сетки-------------

h=1/M; t=1/N;

%--------------------Константы-----------------------

 

if t>h,clc,for i=1:10,disp(' ');,end;

disp(' Возможна неустойчивость!!!');

disp(' (Не выполнено условие Куранта-Леви:t<=h)!!!');

pause,end;,g=(t/h)^2;

u=zeros(M+1,N+1);

g=t/h;

g2=g^2;

t2=t^2;

h2=h^2;

%------------первое начальное условие

for i=0:M, u(i+1,1)=9*sin(5*pi*i*h/2); end

%------------первое граничное условие

for j=1:N, u(1,j+1)=sin(5*pi*j*h/2); end

%%------------заполнение матрицы

for i=1:M-1, u(i+1,2)=9*sin(5*pi*i*h/2)+5*(pi/2)*t*cos(5*pi*i*h/2)+(t2/2)*((u(i,1)-2*u(i+1,1)+u(i+2,1))/h2); end

u(M+1,2) =g2*(u(M,1)-u(M+1,1))+9;

for j=1:N-1,

for i=1:M-1,

u(i+1,j+2)=2*(1-g2)*u(i+1,j+1)+g2*(u(i,j+1)+u(i+2,j+1))-u(i+1,j);

end;

u(M+1,j+2) =2*(1-g2)*u(M+1,j+1)-u(M+1,j)+2*g2*u(M,j+1)-5*h*pi*sin(5*pi*t*j/2)*g2;

end;

%-------------------построение графиков-----------

contour(u,40);pause;

mesh(u);pause;

for t=1:60:360

view(t,50);

pause;

end

 

Неявная схема.

 

%------ определение числа разбиений по осям x, t -----

M=50; N=60;

%--- определение шагов сетки по оси x или t

h=1/M; t=1/N;

%----------- определение рабочих констант ----------

u=zeros(M+1,N+1);

h2=h^2; t2=t^2; g2=t2/h2;

%-----заполнение матрицы U(x,t) 1-ым начальным условием -

for i=0:M, u(i+1,1)=9*sin(5*pi*i*h/2); end

A=zeros(M,1);C=zeros(M+1,1);B=A;A1=A;F=C;B1=C;

%--- этап заполнения матрицы U(x,t) 2-ым начальным условием

%----------1) Определение прогоночных коэффициентов---------

for i=1:M-1, A(i)=g2/2; B(i+1)=g2/2; C(i+1)=1+g2; F(i+1)=9*sin(5*pi*i*h/2)+t*5*(pi/2)*cos(5*pi*i*h/2);

end;

%-----2) Определение граничных прогоночных коэффициентов----

A(M)=g2; B(1)=0; C(1)=1; C(M+1)=1+g2;

F(1)=sin(5*pi*t/2); F(M+1)=9*sin(5*pi*M*h/2)+t*5*(pi/2)*cos(5*pi*M*h/2);

%------------ определение U(i,1) методом прогонки ---------

A1(1)=B(1)/C(1); B1(1)=F(1)/C(1);

for i=2:M

A1(i)=B(i)/(C(i)-A(i-1)*A1(i-1));

B1(i)=(F(i)+A(i-1)*B1(i-1))/(C(i)-A(i-1)*A1(i-1));

end;

B1(M+1)=(F(M+1)+A(M)*B1(M))/(C(M+1)-A(M)*A1(M));

u(M+1,2)=B1(M+1);

for i=M:-1:1,

u(i,2)=A1(i)*u(i+1,2)+B1(i);

end;

%------------ этап заполнения матрицы U(x,t) --------------

%-----------1) Определение прогоночных коэффициентов-------

for i=1:M-1, A(i)=g2; B(i+1)=g2; C(i+1)=1+2*g2; end

%-------2) Определение граничных прогоночных коэффициентов--

A(M)=2*g2; B(1)=0; C(1)=1; C(M+1)=1+2*g2;

%------- определение U(i,j) методом прогонки -------

A1(1)=B(1)/C(1);

for i=2:M,

A1(i)=B(i)/(C(i)-A(i-1)*A1(i-1));

end;

for j=2:N,

F(1)=sin(5*pi*j*t/2);

for i=1:M-1,

F(i+1)=2*u(i+1,j)-u(i+1,j-1)+8*t2*(t2*j^2+h2*i^2);

end;

F(M+1)=2*u(M+1,j)-u(M+1,j-1);

B1(1)=F(1)/C(1);

for i=2:M,

B1(i)=(F(i)+A(i-1)*B1(i-1))/(C(i)-A(i-1)*A1(i-1));

end;

B1(M+1)=(F(M+1)+A(M)*B1(M))/(C(M+1)-A(M)*A1(M));

u(M+1,j+1)=B1(M+1);

for i=M:-1:1,

u(i,j+1)=A1(i)*u(i+1,j+1)+B1(i);

end;

end;

contour(u,40);

pause;

mesh(u);

pause;

for t=1:60:360

view(t,50);

pause;

end

 

Результаты работы.

 

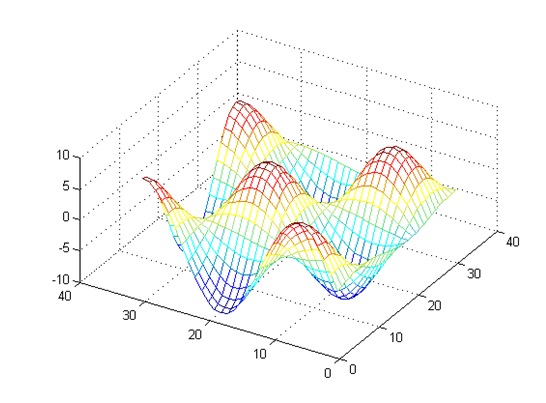Явная схема.

Columns 1 through 7

 

0 0.7071 1.0000 0.7071 0.0000 -0.7071 -1.0000

6.3640 5.9058 3.9916 1.0265 -2.4288 -5.5747 -7.4445

9.0000 7.8284 4.6187 0.2428 -4.1613 -7.5711 -9.2727

6.3640 5.1653 2.6218 -0.6042 -3.6568 -5.7239 -6.3161

0.0000 -0.5236 -0.9109 -1.0610 -0.9349 -0.5582 -0.0134

-6.3640 -5.9058 -3.9100 -0.8963 2.3508 4.9858 6.3260

-9.0000 -7.8284 -4.6187 -0.2065 4.2594 7.6164 8.9897

-6.3640 -5.1653 -2.6218 0.6042 3.6729 5.7837 6.3811

-0.0000 0.5236 0.9109 1.0610 0.9310 0.5459 0.0009

6.3640 5.9058 3.9100 0.8874 -2.3848 -5.0518 -6.4069

9.0000 7.8284 4.5988 0.1523 -4.3389 -7.6976 -9.0536

 

Columns 8 through 14

 

-0.7071 -0.0000 0.7071 1.0000 0.7071 0.0000 -0.7071

-7.2626 -4.8717 -0.9038 3.4214 6.7401 8.0198 6.9107

-8.8477 -6.1953 -1.7106 3.5779 8.1855 10.6647 10.1477

-5.4212 -3.3963 -0.7087 2.2022 4.8421 6.5682 6.7306

0.5477 0.8937 0.7957 0.2168 -0.5574 -1.0465 -0.9192

6.0326 4.1846 1.2181 -2.2080 -5.3155 -7.2744 -7.3599

8.0198 4.9588 0.6065 -3.9159 -7.4893 -9.2871 -8.9067

5.3023 2.8274 -0.3877 -3.4888 -5.6678 -6.3990 -5.5833

-0.5564 -0.9694 -1.1256 -0.9869 -0.5888 -0.0304 0.5271

-6.0904 -4.1883 -1.2000 2.0987 4.8509 6.3362 6.1639

-8.0569 -4.9631 -0.5761 3.9545 7.4401 8.9732 8.1622

 

Columns 15 through 16

 

-1.0000 -0.7071

3.8545 -0.1063

6.6733 1.2078

5.0118 1.6908

-0.2546 0.5215

-5.2704 -1.4367

-6.3619 -2.0728

-3.5289 -0.7768

0.8741 0.8199

4.3745 1.4078

5.2259 0.9282

 

 

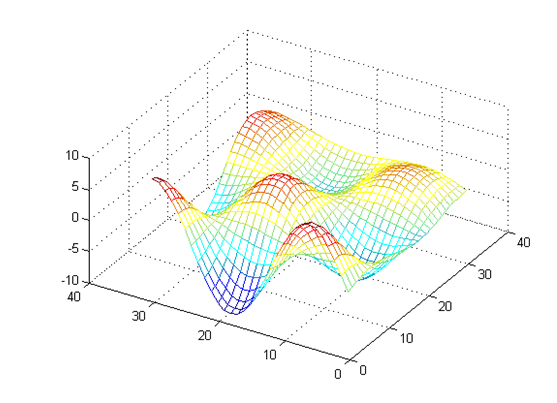
Неявная схема

Columns 1 through 7

 

0 0.5000 0.8660 1.0000 0.8660 0.5000 0.0000

6.3640 5.9643 4.4466 2.3626 0.2457 -1.4906 -2.5995

9.0000 7.9643 5.5092 2.4473 -0.4554 -2.6345 -3.8011

6.3640 5.3035 3.3734 1.1606 -0.8074 -2.1622 -2.7407

0.0000 -0.4633 -0.7276 -0.7726 -0.6214 -0.3265 0.0464

-6.3640 -5.9585 -4.3954 -2.2281 -0.0125 1.8107 2.9836

-9.0000 -7.9633 -5.4799 -2.3474 0.6793 3.0361 4.4250

-6.3640 -5.3029 -3.3394 -1.0382 1.0984 2.7168 3.6468

-0.0000 0.4659 0.7912 0.9882 1.1024 1.1835 1.2674

6.3640 5.9753 4.5527 2.6716 0.8634 -0.4846 -1.1695

9.0000 8.0693 5.9217 3.2553 0.7180 -1.1912 -2.1917

 

Columns 8 through 14

 

-0.5000 -0.8660 -1.0000 -0.8660 -0.5000 -0.0000 0.5000

-3.0032 -2.7633 -2.0352 -1.0204 0.0755 1.0731 1.8384

-3.9379 -3.2358 -2.0017 -0.5660 0.7895 1.8732 2.5932

-2.5760 -1.8466 -0.8033 0.3031 1.2772 2.0073 2.4662

0.4334 0.7833 1.0651 1.2714 1.4170 1.5337 1.6618

3.4443 3.2942 2.7389 2.0215 1.3644 0.9314 0.8102

4.8150 4.3881 3.4524 2.3509 1.3846 0.7619 0.5801

3.8923 3.5921 2.9635 2.2431 1.6368 1.2859 1.2530

1.3730 1.5065 1.6676 1.8541 2.0637 2.2939 2.5423

-1.1660 -0.5905 0.3537 1.4356 2.4482 3.2459 3.7613

-2.2387 -1.4880 -0.2239 1.2263 2.5691 3.5985 4.2201

 

Columns 15 through 16

 

0.8660 1.0000

2.2914 2.4083

2.9437 2.9793

2.6921 2.7583

1.8391 2.0909

1.0144 1.4980

0.8323 1.4337

1.5279 2.0466

2.8072 3.0886

4.0026 4.0367

4.4468 4.3738

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ :

 

 

1. В.Г. Долголаптев, В.Н. Земсков. Численные методы решения разностных

уравнений математической физики. Методические указания к курсовой работе

по высшей математике., МИЭТ 1987.

 

2. Сборник задач по математике. т.4 Методы оптимизации. Уравнения в

частных производных. Интегральные уравнения. под ред. А.В. Ефимова.,

М. Наука 1990.