Реакция систем на случайные сигналы [2,14].
Если сигнал на входе линейной системы является детерминированным, то, при известных параметрах системы, его соотношение с выходным сигналом является однозначным. Таким же однозначным является соотношение процессов на входе и выходе и для случайных сигналов, однако в силу природы последних явное представление, как входного сигнала, так и отклика системы, не представляется возможным. Для описания отклика системы необходимо использовать статистический подход. При рассмотрении данной темы ограничимся только физически реализуемыми системами с односторонним импульсным откликом h(t) (h(t)=0 при t<0) и соответствующей частотной характеристикой H(f). Если параметры входного сигнала специально не оговариваются, то по умолчанию принимается, что на вход системы поступает реализация случайного стационарного процесса x(t) с нулевым средним и вызывает сигнал y(t) на выходе системы.
Квазидетерминированный сигнал в какой-то мере позволяет оценить сохранение однозначности преобразования системой случайных сигналов.
Допустим, что система имеет импульсный отклик h(t) = exp(-at), t ³ 0. Квазидетерминированный случайный сигнал стационарен, не обладает свойством эргодичности, но может быть описан в явной математической форме. Зададим сигнал на входе системы следующего вида:
x(t) = A + cos(2t+j),
где A и j - взаимно независимые случайные величины, причем j равномерно распределена в интервале [0, 2p]. Выходной сигнал определится выражением:
y(t) = h(t) * x(t-t) º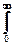 
h(t)×x(t-t) dt = A/3 + [3 cos(2t+j) + 2 sin(2t+j)]/13.
Из выражения следует, что выходной сигнал системы также является случайным процессом и содержит те же самые случайные параметры, что и входной сигнал, а, следовательно, для него также могут быть определены статистические характеристики.
Математическое ожиданиепроизвольного случайного стационарного сигнала x(t) на выходе линейной системы определится выражением:
= М{y(t)}= 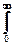M{x(t-t)}×h(t) dt =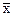
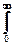h(t) dt = 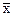Кпс. (11.5.1)
Отсюда следует, что математическое ожидание выходных сигналов системы равно математическому ожиданию входных сигналов, умноженному на коэффициент усиления системой постоянной составляющей. Если система не пропускает постоянную составляющую сигналов (площадь или сумма коэффициентов импульсного отклика системы равна нулю), то случайный выходной сигнал всегда будет иметь нулевое математическое ожидание.
Корреляционные соотношения.Для произведения выходных сигналов y(t) и y(t+t) линейной системы можно записать:
y(t)×y(t+t) =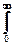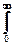h(a)h(b) x(t-a)x(t+t-b) da db.
Если взять математические ожидания от обеих частей этого равенства, то, с учетом соотношения в подынтегральном выражении
M{x(t-a) x(t+t-b)} = -Rx(t-a-t-t+b) = Rx(t+a-b),
получим:
Ry(t) =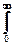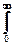h(a)h(b) Rx(t+a-b) da db º Rx(t) * h(t+a) * h(t-b). (11.5.2)
Таким образом, функция автокорреляции (АКФ) выходного сигнала равна АКФ входного сигнала, свернутой дважды, в прямом и обратном направлении, с импульсным откликом системы, что сохраняет четность АКФ выходного сигнала. Для нецентрированных процессов аналогичное заключение действительно и для ковариационных функций.
Заметим, что для свертки импульсных откликов, производя замену t-b = t, мы имеем равенство:
h(t+a) * h(t-b) = h(t+a+b) * h(t) = h(t) * h(t+g) = Kh(t),
где Kh(t) - функция ковариации импульсного отклика системы. Отсюда:
Ry(t) = Rx(t) * Kh(t). (11.5.2')
Это означает появление в случайном сигнале на выходе системы определенной корреляционной зависимости, вызванной инерционностью системы, причем радиус корреляции выходного сигнала обратно пропорционален верхней частоте, пропускаемой системой.
Для взаимной корреляционной функции (ВКФ) Rxy входного и выходного сигналов соответственно имеем:
x(t)×y(t+t) =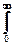h(a) x(t)y(t+t-a) da.
Rxy(t) =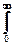h(a) Rx(t-a) da º Rx(t) * h(t-a). (11.5.3)
т.е. функция взаимной корреляции входного и выходного сигналов равна свертке АКФ входного сигнала с функцией импульсного отклика системы - фильтрации АКФ сигнала этим же фильтром. Заключение действительно и для функций ковариации.
Другая взаимно корреляционная функция Ryx может быть получена из соотношения:
Ryx(t) = Rxy(-t) º Rx(t) * h(t+a). (11.5.4)
Отметим, что для статистически независимых случайных величин при одностороннем импульсном отклике h(t)=0 при t<0 функция Rxy(t) также является односторонней и равна 0 при t<0, а функция Ryx соответственно равна 0 при t>0.