Проверка гипотезы о равенстве центров распределения математического ожидания 2-х нормальных генеральных совокупностей.

Задача имеет большой практический интерес. Достаточно часто наблюдается такая ситуация, что средний результат в одной серии эксперимента отличается от среднего результата в другой серии эксперимента.

Возникает вопрос: можно ли объяснить отличительное расхождение случайными ошибками эксперимента и относительно малыми объёмами выборки или это отклонение вызвано какими-либо неизвестными, незамеченными закономерностями.

Имеется две случайных величин Х и Y с нормальным законом распределения.

Получим 2-е независимых выборки объёмом n₁ и n₂ из указанных генеральных совокупностей.

Необходимо проверить: Н₀: М(X) = М(Y)

H₁: |M(X) – M(Y)| > 0

Рассмотрим два случая:

1. – известны дисперсия генеральной совокупности ;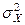

2. – дисперсия неизвестна .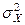

1 - 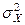,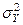M(X) и M(Y) - неизвестны, для их оценки мы используем средние выборочные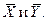

Относительно 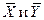известно, что они подчиняются нормальному закону распределения с параметрами:

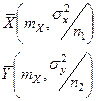
Рассмотрим случайную величину 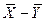. В силунезависимости выборок эта случайная величина подчиняется нормальному закону распределения.

Её дисперсия:

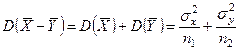
Если гипотез Н₀ верна(справедлива), то тогда: .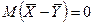

Величина:

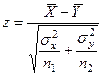с параметрами (0, 1)

Выбирая уровень значимости α или доверительную вероятность Р = 1- α можем записать:

; ;

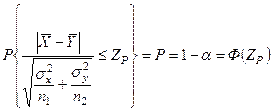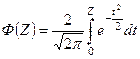Выбирая по величине интеграла вероятности значения Z_P мы тем самым делим выборочных данных на область допустимых значений и критическую область.

Для области, где выполняется неравенство |Z| ≤ Z_P – область допустимых значений(ОДЗ) Н₀ – принимается.

А, если |Z| > Z_P – критическая область(КО) Н₀ – отвергается, Н₁ – принимается.

Чем меньше α, тем меньше вероятность отклонить проверяемую гипотезе, если она верна. Но в этом случае увеличивается вероятность совершения ошибки II-го рода.

Чем меньше α, тем больше ОДЗ и тем больше вероятность принять проверяемую гипотезу, если она не верна, т.е. совершить ошибку II-го рода.

Методы проверки гипотез позволяют только отвергнуть проверяемую гипотезу, но они не могут доказать её справедливость.

2 -Дисперсия неизвестна.

Есть 2-е случайных величины X и Y, .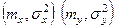

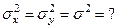m_x и m_y неизвестны берутся независимые выборки (n₁;n₂) и рассматривается гипотеза: Н₀: M(X) = M(Y)

H₁: |M(X) – M(Y)| > 0.

Для оценки математического ожидания M(X) и M(Y) используем среднее выборочное . Для оценки дисперсий используем:

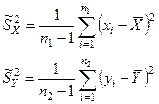- несмещённые, состоятельные оценки дисперсии.

Поскольку генеральные совокупности X и Y имеют одинаковые дисперсии, то для оценки дисперсии 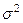целесообразно использовать результаты обеих выборок.

Наиболее целесообразной оценкой дисперсии является средняя взвешенная этих двух оценок.

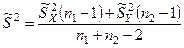
Если гипотеза Н₀ справедлива, то тогда случайная величина 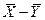подчиняется нормальному закону распределения с 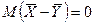и с дисперсией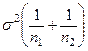

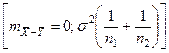
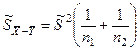
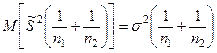
Если построить случайную величину:

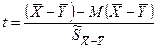
, то она будет подчиняться нормальному закону с параметрами (0; 1).

Т.к. 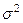неизвестна, то такая величина подчиняется t-распределению Стьюдента(со степенями свободы n₁+ n₂– 2).

Для α(Р = 1– α) подсчитывается критическое значение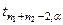

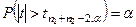
Если вычисленные значения 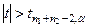, то гипотеза Н₀ отвергается и наоборот:

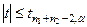Н₀ принимается.

Проверка гипотезы о совпадении 2-х дисперсий.

Задача имеет важное практическое значение. Возникает при наладке какого-либо оборудования при сравнении точности приборов, инструментов, методов измерений.

По 2-м независимым выборкам вычислены оценки дисперсий:

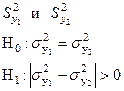
Для проверки гипотезы Н₀ используется критерий Фишера(F–критерий, F–распределение).

Вычисляется коэффициент:

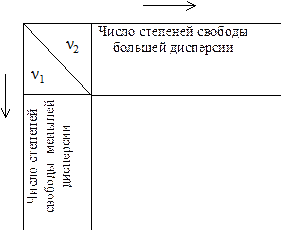
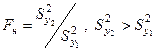
Вычисляется критическое значение F_кр(α (или Р = 1 - α))

,где: ν – число степеней свободы числителя и знаменателя.

Если F_н > F_кр, то Н₀ отвергается,

F_н < F_кр, то Н₀ принимается.

Анализ однородности дисперсий.

Понятие однородности является обобщением понятия равенства дисперсий в случае, если число выборок превосходит 2(N > 2).

Для проверки гипотезы H₀:

Н₀: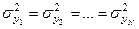

Н₁: дисперсия неоднородна.

Объёмы выборок n₁,n₂, … ,n_N различны.

Когда объёмы выборок различны для решения задачи является χ² с (N-1) степенями свободы.

На практике наиболее частым является когда объёмы выборок одинаковы.

При равных объёмах выборок используется критерий Кохрана для проверки Н₀.

Есть соответствующее распределение, но оно громоздко.

В начале вычисляется фактическое значение критерия:

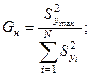
Отношение максимальной оценки дисперсии к сумме всех оценок дисперсий вычисленных по табличным данным.

Для Р = 1 – α вычисляется критическое значение критерия Кохрана G_кр.

При G_н ≤ G_кр - H₀ принимается;

G_н > G_кр - H₀ отвергается.

Проверка гипотез о законе распределения.

Имеется случайная величина Х, требуется проверить гипотезу Н₀:

Н₀: эта случайная величина подчиняется некоторому закону распределения F(x).

Для проверки гипотезы делается выборка состоящая из n независимых наблюдений над случайной величиной Х. По выборке строится эмпирическая функция распределения F*(x). Сравнивая эти распределения с помощью некоторого критерия(критерий согласия) делается вывод о том, что эти два распределения согласуются, т.е. Н₀ – принимается.

Существует несколько критериев согласия: χ² Пирсона, критерий Колмогорова и т.д.

Критерий согласия χ² Пирсона.

Имеется случайная величина Х, выдвигается гипотеза Н₀: F(x), делается выборка.

Диапазон Х_min – Х_max разбивается на ℓ интервалов. Размер интервала определяется по правилу Старджесса. D₁;D₂;D₃;…;D_ℓ.

Интервал D_i	D₁	D₂	D₃	…	D_ℓ
Эмпирическая частота m_i	m₁	m₂	m₃	…	m_ℓ
Теоретическая частота np_i	np₁	np₂	np₂	…	np_ℓ

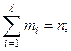
m_i > 3(в среднем 5 - 7).

При m_i < 3 укрупнить интервал.

Находим частоту попадания случайной величины внутрь каждого интервала.

Поскольку теоретическое распределение задано в гипотезе Н₀ всегда можно найти вероятность p_i попадания случайной величины внутрь каждого интервала.

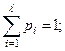
χ² Пирсона предполагает, что надо построить:

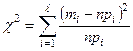
(имеет распределение χ² только при относительно больших n (n > 50)).

Порядок применения χ² Пирсона:

1. Рассчитывается эмпирическое значение критерия χ²;

2. Выбирается уровень значимости α (при Р = 1 - α);

3. По таблице подсчитывается ,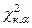

где: α – уровень значимости;

к – число степеней свободы.

В общем случае к = ℓ - r – 1,

где: ℓ - количество интервалов разбиения;

r – количество параметров распределения подсчитанных по выборке;

Здесь к = r – 1.

Если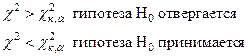

Критерий Колмогорова.

По результатам выборки объёмом n строится эмпирическая функция распределения F(х). Принимается гипотеза Н₀: случайная величина Х подчиняется распределению описанному функцией F(x).

За меру расхождения функций принимается величина:

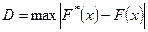
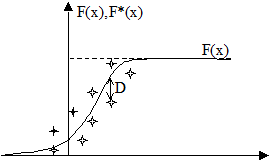
Существуют таблицы распределения Колмогорова в которых можно найти:

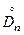- критическое значение. Оно зависит от уровня значимости α(Р = 1 - α), величины D и величины выборки n.

Если полученные из опыта значения коэффициента D оказывается больше критического 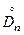, то Н₀ отвергается.

Если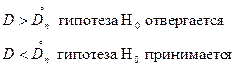

С помощью величины 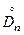можно построить доверительные границы для неизвестной функции F(x):

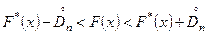
Колмогоров показал, что при n → ∞ величина:

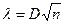
подчиняется распределению Колмогорова.

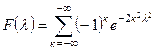
Критерий Колмогорова так же может быть использован для статистической проверки принадлежности двух выборок объёмом n₁ и n₂ к одной и той же генеральной совокупности. Вычисляется параметр λ:

где: 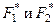- эмпирические функции распределения соответственно первой и второй выборки.

По величине λ судят о согласии.