Определение эмпирического корреляционного соотношения.

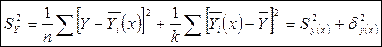
y – измеряемое значение зависимой переменной

n – общее количество измерений

- условное среднее (среднее значение зависимой переменной у в i-ом интервале св Х)

k – общее количество интервалов

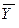- среднее всей совокупности измерений

В пределах каждого интервала, для всех тех значений Х, для которых есть экспериментальные результаты (значения Y), находим средние значения.

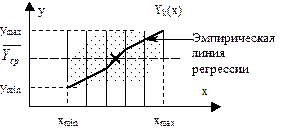S_y(x)² – составляющая полной дисперсии, характеризует дисперсию результатов измерений относительно эмпирической линии регрессии, т.е. влияние прочих факторов на зависимую переменную Y.

d_y(x­)² – характеризует дисперсию эмпирической линии регрессии относительно среднего всей совокупности, т.е. влияние исследуемого фактора на зависимую переменную Y.

- Эмпирическое корреляционное соотношение

Из сравнения с формулой для теоретического корреляционного соотношения видно: при расчете теоретического корреляционного соотношения необходимо знать форму связи между переменными.

При вычислении эмпирического корреляционного соотношения никакие предположения о форме связи не используются, нужна только эмпирическая линия регрессии.

Свойства:

1. 0 £ £ 1

2. если =1, все точки корреляционного поля лежат на линии регрессии – функциональная связь между Х и Y.

3. Если =0 (когда 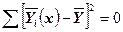), отсутствует изменчивость условных средних 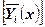, эмпирическая линия регрессии проходит параллельно оси абсцисс – свзи между Х и Y нет.

Эмпирическое корреляционное соотношение завышает тесноту связи между переменными и случайными величинами, причем тем сильнее, чем меньше число измерений, поэтому рекомендуется использовать для предварительной оценки тесноты связи, а для окончательной оценки – теоретическое корреляционное соотношение.

Коэфициент корреляции.

Рассмотрим случай вычисления теоретического корреляционного соотношения , когда связь между случайными величинами Х и Y является линейной.

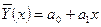
Такая форма связи между Х и Y имеет место в случае, когда случайные величины подчиняются двуменому нормальному закону распределения.

Подставив вместо Y и 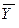их значения для случая линейной зависимости:

=

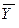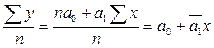
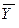(х)=а₀ + а₁х

=

Заменим а₁ ее значением, полученным из решения нормальных уравнений:

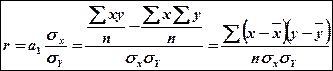
Коэфициент корреляции является частным случаем теоретического корреляционного соотношения , когда связь между СВ является линейной. В этом случае r является показателем тесноты связи.

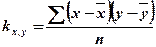- выборочный корреляционный момент

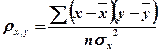
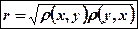
Выборочный коэфициент корреляции обладает свойствами:

1. r=0, если св Х и Y независимы

2. 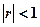- Для любых св Х и Y

3. 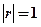- Для случая линейной зависимости св Х и Y.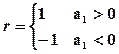

Коэфициент корреляции используется для оценки тесноты связи и в случае нелинейной зависимости между случайными величинами.

Если предварительный графический анализ поля корреляции указывает на какую либо тесноту связи, полезно вычислить коэфициент корреляции.

Если модуль коэфициента корреляции 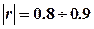, то независимо от вида связи можно считать, что она достаточно тесна, чтобы исследоват ее форму.

Двумерное нормальное распределение.

Его возникновение объясняется центральной предельной теоремой Ляпунова:

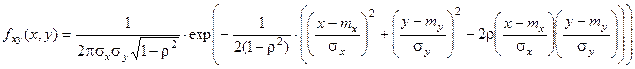
r – коэффициент корреляции. Х и У по отдельности распределены нормально (m_x,s_x) и (m_y,s_y).

В частном случае независимых СВ Х и У r=0:

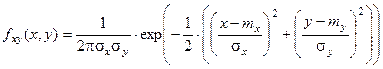
Исходные плотности одномерных нормальных распределений Х и У:

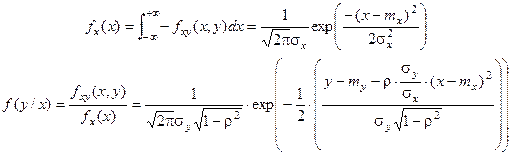
Условное распределение – нормальное с условиям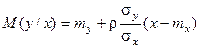и:

и .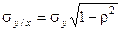

Первое условие является уравнением функции регресси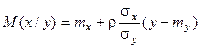и.

и .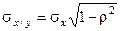

Нормальная регрессия прямолинейна. Точность оценки у/х одинакова для всех х. В качестве меры тесноты связи используется коэффициент корреляции, а форму связи при этом характеризует коэффициент регрессии.

Z=f_xy(x,y) – трехмерная поверхность, сечения которой плоскостями XZ и YZ представляют собой графики плотности одномерных распределений.