A1+A2+…+An=W

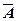-событие противоположное событию А, если оно состоит в не появлении события А.

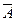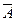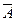А и - полная группа событий, т.к. А+=W, А=Æ.

 

Теорема сложения вероятностей.

 

Вероятность суммы несовместных событий равна сумме вероятностей событий:

Р(А+В+С+…) = Р(А) + Р(В) + Р(С) +…

Следствие. Если события A₁+A₂+…+A_n - полная группа событий, то сумма их вероятностей равна 1.

P(A+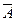) = P(A) + P(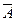) = 1

Вероятность наступления двух совместных событий равна:

Р(А+В) = Р(А) + Р(В) - Р(АВ)

 

Р(А+В+С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) – Р(АВС)

 

 

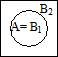
Теорема. Если АÌВ, то Р(А) £ Р(В).

В=В₁+В₂ (В₁=А) Р(В)=Р(В₁) + Р(В₂)= Р(А) + Р(В₂)

 

Теорема умножения вероятностей. Условные вероятности.

Опыт повторяется n раз, m_B раз наступает событие В, m_АВ раз наряду с событием В наступает событие А.

hn(B) = hn(AB) =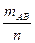

Рассмотрим относительную частоту наступления события А, когда событие В уже наступило:

- условная вероятность события А по событию В – вероятность события А, когда событие В уже наступило.

Свойства условных вероятностей.

Свойства условных вероятностей аналогичны свойствам безусловных вероятностей.

1. 0 £ Р(А/В) £ 1, т.к. 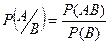; АВ Ì В, Р(АВ) £ Р(В)

2. Р(А/А)=1

3. ВÌА, è Р(А/В)=1

4.

5. Р[(A+C)/B] = Р(А/В) + Р(C/В) – Если события А и С несовместны

Р[(A+C)/B] = Р(А/В) + Р(C/В) - Р(АC/В) – Если события А и С совместны

 

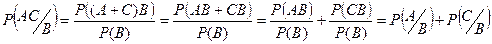
Теорема. Вероятность произведения двух событий равна произведению вероятности одного события на условную вероятность другого.

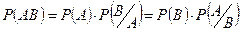
Свойства независимых событий.

Если события А и В независимы, то независимы и каждая из пар: А и В, А и , 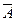и В, .

Если события Н₁, Н₂, …Н_n независимы, то заменяя любые из них на противоположные, вновь получаем независимые события.

 

Формула полной вероятности.

Вероятность события В, которое может произойти совместно только с одним из событий Н₁, Н₂, …Н_n , образующих полную группу событий, вычисляется по формуле:

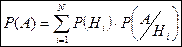
События А₁, А₂, …А_n называют гипотезами.

 

Теорема гипотез (формула Байеса).

Если до опыта вероятности гипотез были Р(Н₁), Р(Н₂)…Р(Н_N), а в результате опыта произошло событие А, то условные вероятности гипотез находятся по формуле:

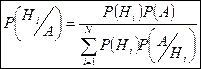
Пример. На трех технологических линиях изготавливаются микросхемы. Найти: 1) вероятность того, что случайно выбранное изделие оказывается бракованным; 2) вероятность того, что если изделие дефектно, то оно изготовлено на 1 линии.

№ линии	Количество изготавливаемых микросхем	Вероятность брака
	25%	5%;
	35%	4%
	40%	2%

Рассмотрим события: Н₁, Н₂,…Н_i,…,Н_N (полная группа событий)– изделие изготавливается i линией; А{изделие с браком}.

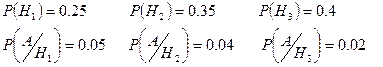
1) Р(А)=0,25*0,05+0,35*0,04+0,4*002=0,0345=3,45%

2)

 

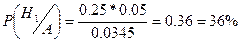
Схема последовательных испытаний Бернулли.

Проводится серия из n испытаний, в каждом из которых с вероятностью р может произойти событие А, с вероятностью q=1-р событие .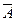

Вероятность наступления события А не зависит от числа испытаний n и результатов других испытаний.

Такая схема испытаний с двумя исходами (событие А наступило либо не наступило) называется схемой последовательных испытаний Бернулли.

Пусть при n испытаниях событие А наступило k раз, (n-k) раз событие .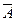

- число различных комбинаций события А

Вероятность каждой отдельной комбинации:

Вероятность того, что в серии из n испытаний событие А, вероятность которого равна р, появится k раз: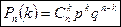

- условие нормировки.

Пример. Вероятность изготовления нестандартной детали равна р=0,25, q=0.75. Построить многоугольник распределения вероятностей числа нестандартных деталей среди 8 изготовленных.

N=8 p=0.25 q=0.75

 

Если k₀ – наивероятнейшее число, то оно находится в пределах:

np-q £ k₀ £ np+q