ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН

Лекция 7.

Основные числовые характеристики дискретных и непрерывных случайных величин: математическое ожидание, дисперсия и среднее квадратическое отклонение. Их свойства и примеры.

Закон распределения (функция распределения и ряд распределения или плотность веро-ятности) полностью описывают поведение случайной величины. Но в ряде задач доста-точно знать некоторые числовые характеристики исследуемой величины (например, ее среднее значение и возможное отклонение от него), чтобы ответить на поставленный во-прос. Рассмотрим основные числовые характеристики дискретных случайных величин.

 

Математическое ожидание.

М(Х) = х1р1 + х2р2 + … + хпрп . (7.1) Если число возможных значений случайной величины бесконечно, то , если… Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему…

Числовые характеристики непрерывных случайных величин.

  Определение 7.7. Математическим ожиданием непрерывной случайной величины… (7.13)

Стандартные законы распределения.

Для дискретной случайной величины Х, представляющей собой число появлений события А в серии из п независимых испытаний (см. лекцию 6), М(Х) можно… Следовательно, М(Хi) = p. Тогда Аналогичным образом вычислим дисперсию: D(Xi) = 0²·q + 1²·p – p²= p – p² = p(1 – p),…

Лекция 8.

Случайные векторы (системы нескольких случайных величин). Закон распределения веро-ятностей дискретной двумерной случайной величины. Функция распределения и плот-ность распределения двумерной случайной величины, их свойства. Вероятность попада-ния случайной точки в произвольную область. Отыскание плотностей вероятности со-ставляющих двумерной случайной величины. Равномерное распределение на плоскости.

Наряду с одномерными случайными величинами, возможные значения которых определяют-ся одним числом, теория вероятностей рассматривает и многомерные случайные величины. Каждое возможное значение такой величины представляет собой упорядоченный набор нескольких чисел. Геометрической иллюстрацией этого понятия служат точки п-мерного пространства, каждая координата которых является случайной величиной (дискретной или непрерывной), или п-мерные векторы. Поэтому многомерные случайные величины называют еще случайными векторами.

 

Двумерные случайные величины.

  Закон распределения дискретной двумерной случайной величины (Х, Y) имеет вид…  

Условные законы распределения составляющих

Дискретной двумерной случайной величины.

. Таким же образом можно найти вероятности возможных значений Х при условии, что… . (8.5)

Условные законы распределения составляющих

Дискретной двумерной случайной величины.

Определение 8.3. Условной плотностью φ(х/у)распределения составляющих Х при данном значении Y = у называется

. (8.6)

Аналогично определяется условная плотность вероятности Y при Х = х:

. (8.6`)

Равномерное распределение на плоскости.

Найдем двумерную функцию распределения: при a < x < b, c < y < d, F(x, y) = 0 при x ≤ a или y… Функции распределения составляющих, вычисленные по формулам, приведенным в свойстве 4 функции распределения, имеют…

Лекция 9.

Некоторые числовые характеристики одномерных случайных величин: начальные и центральные моменты, мода, медиана, квантиль, коэффициенты асимметрии и эксцесса. Числовые характеристики двумерных случайных величин: начальные и центральные моменты. Корреляционный момент и коэффициент корреляции. Коррелированность и зависимость случайных величин.

Определение 9.1. Начальным моментом порядка kслучайной величины Х называется матема-тическое ожидание величины X^k:

ν_k = M (X^k). (9.1)

В частности, ν₁ = М(Х), ν₂ = М(Х²). Следовательно, дисперсия D(X) = ν₂ – ν₁².

Определение 9.2. Центральным моментом порядка kслучайной величины Х называется мате-матическое ожидание величины (Х – М(Х))^k:

μ_k = M((Х – М(Х))^k). (9.2)

В частности, μ₁ = M(Х – М(Х)) = 0, μ₂ = M((Х – М(Х))²) = D(X).

Можно получить соотношения, связывающие начальные и центральные моменты:

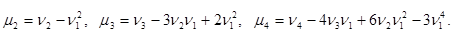
Мода и медиана.

Такая характеристика случайной величины, как математическое ожидание, называется иногда характеристикой положения, так как она дает представление о положении случайной величии-ны на числовой оси. Другими характеристиками положения являются мода и медиана.

Определение 9.3. Модой М дискретной случайной величины называется ее наиболее вероятное значение, модой Мнепрерывной случайной величины – значение, в котором плотность вероятности максимальна.

Пример 1.

Если ряд распределения дискретной случайной величины Х имеет вид:

Х
р	0,1	0,7	0,15	0,05

то М = 2.

Пример 2.

Для непрерывной случайной величины, заданной плотностью распределения 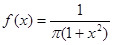, модой является абсцисса точки максимума: М = 0.

Замечание 1. Если кривая распределения имеет больше одного максимума, распределение называется полимодальным, если эта кривая не имеет максимума, но имеет минимум – анти-модальным.

Замечание 2. В общем случае мода и математическое ожидание не совпадают. Но, если распре-деление является симметричным и модальным (то есть кривая распределения симметрична от-носительно прямой х = М) и имеет математическое ожидание, оно совпадает с модой.

Определение 9.4. Медианой Ме непрерывной случайной величины называют такое ее значение, для которого

p( X < Me ) = p( X > Me ). (9.3)

Графически прямая х = Ме делит площадь фигуры, ограниченной кривой распределения, на две равные части.

Замечание. Для симметричного модального распределения медиана совпадает с математичес-ким ожиданием и модой.

Определение 9.5. Для случайной величины Х с функцией распределения F(X) квантилью порядка р (0 < p < 1) называется число К_р такое, что F(K_p) ≤ p, F(K_p + 0) ≥ p. В частности, если F(X) строго монотонна, К_р: F(K_p) = p.

Асимметрия и эксцесс.

Если распределение не является симметричным, можно оценить асимметрию кривой распреде-ления с помощью центрального момента 3-го порядка. Действительно, для симметричного распределения все нечетные центральные моменты равны 0 ( как интегралы от нечетных функ-ций в симметричных пределах), поэтому выбран нечетный момент наименьшего порядка, не тождественно равный 0. Чтобы получить безразмерную характеристику, его делят на σ³ (так как μ₃ имеет размерность куба случайной величины).

Определение 9.6. Коэффициентом асимметриислучайной величины называется

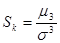
. (9.4)

Рис.1. Рис.2.

В частности, для кривой, изображенной на рис.1, S_k > 0, а на рис.2 - S_k < 0.

Для оценки поведения кривой распределения вблизи точки максимума (для определения того, насколько «крутой» будет его вершина) применяется центральный момент 4-го порядка.

Определение 9.7. Эксцессом случайной величины называется величина

(9.5)

Замечание. Можно показать, что для нормального распределения , и, соответственно, Ех = 0. Для кривых с более острой вершиной Ех >0, в случае более плоской вершины Ех < 0.

Числовые характеристики двумерных случайных величин.

Определение 9.8. Начальным моментом порядка k, s двумерной случайной величины (Х, Y) называется математическое ожидание произведения Xk на Ys: αk,s = M (XkYs). (9.6) Для дискретных случайных величин для непрерывных случайных величин

Корреляционный момент и коэффициент корреляции.

Kxy = μ1,1 = M((X – M(X))(Y – M(Y))). (9.8) Для дискретных случайных величин для непрерывных случайных величин Безразмерной характеристикой коррелированности двух случайных величин является коэффи-циент корреляции

Лекция 10.

Функции от случайных величин. Функция одного случайного аргумента, ее распределение и математическое ожидание. Функция двух случайных аргументов. Распределение суммы независимых слагаемых. Устойчивость нормального распределения.

В предыдущих лекциях рассматривались некоторые законы распределения случайных величин. При решении задач часто удобно бывает представить исследуемую случайную величину как функцию других случайных величин с известными законами распределения, что помогает уста-новить и закон распределения заданной случайной величины.

Определение 10.1. Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргу-мента Х:Y = φ(X). Выясним, как найти закон распределения функции по известному закону распределения аргумента.

1) Пусть аргумент Х – дискретная случайная величина, причем различным значениям Х соот-ветствуют различные значения Y. Тогда вероятности соответствующих значений Х и Y равны.

Пример 1. Ряд распределения для Х имеет вид: Х 5 6 7 8

р 0,1 0,2 0,3 0,4

Найдем закон распределения функции Y = 2X² - 3: Y 47 69 95 125

р 0,1 0,2 0,3 0,4

(при вычислении значений Y в формулу, задающую функцию, подставляются возможные значения Х).

2) Если разным значениям Х могут соответствовать одинаковые значения Y, то вероятности значений аргумента, при которых функция принимает одно и то же значение, складываются.

Пример 2. Ряд распределения для Х имеет вид: Х 0 1 2 3

р 0,1 0,2 0,3 0,4

Найдем закон распределения функции Y = X² - 2Х: Y -1 0 3

р 0,2 0,4 0,4

(так как Y = 0 при Х = 0 и Х = 2, то р(Y = 0) = р( Х = 0) + р(Х = 2) = 0,1 + 0,3 = 0,4 ).

3) Если Х – непрерывная случайная величина, Y = φ(X), φ(x) – монотонная и дифференцируемая функция, а ψ(у) – функция, обратная к φ(х), то плотность распределения g(y) случайно функции Y равна: (10.1)

Пример 3. 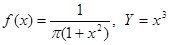. Тогда

Математическое ожидание функции одного случайного аргумента.

1) Если Х – дискретная случайная величина, то (10.2) Пример 3. Найдем M(Y) для примера 1: M(Y) = 47·0,1 + 69·0,2 + 95·0,3 + 125·0,4 = 97.

Функция двух случайных величин. Распределение суммы

Независимых слагаемых.

Определение 10.2. Если каждой паре возможных значений случайных величин Х и Y соответ-ствует одно возможное значение случайной величины Z, то Z… Рассмотрим в качестве такой функции сумму Х + Y. В некоторых случаях можно… 1) Если X и Y – дискретные независимые случайные величины, то для определения закона распределения Z = Х + Y нужно…

Устойчивость нормального распределения.

Определение 10.3. Закон распределения вероятностей называется устойчивым, если компози-ция таких законов есть тот же закон (возможно, отличающийся другими значениями парамет-ров).

В частности, свойством устойчивости обладает нормальный закон распределения: композиция нормальных законов тоже имеет нормальное распределение, причем ее математическое ожидание и дисперсия равны суммам соответствующих характеристик слагаемых.

 

 

Лекция 11.

Нормальный закон распределения на плоскости. Линейная регрессия. Линейная корреляция.

(11.1) Таким образом, нормальный закон на плоскости определяется 5 параметрами: а1,… Следовательно, из некоррелированности составляющих нормально распределенной двумерной случайной величины следует их…

Линейная регрессия.

Y ≈ g(Х) = α + βХ, (11.2) и определим параметры α и β с помощью метода наименьших квадратов. … Определение 11.2. Функция g(Х) = α + βХ называется наилучшим приближениемY в смысле метода наименьших…

Линейная корреляция.

(11.7) для непрерывной случайной величины – . (11.8)

Лекция 12.

Распределения «хи-квадрат», Стьюдента и Фишера. Связь этих распределений с нормаль-ным распределением.

Рассмотрим некоторые распределения, связанные с нормальным и широко применяющиеся в математической статистике.

Распределение «хи-квадрат».

(12.1) является случайной величиной, распределенной по так называемому закону… Плотность этого распределения

Распределение Стьюдента.

(12.3) имеет распределение, называемое t – распределением или распределением… С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.

Распределение F Фишера – Снедекора.

. (12.4) Ее распределение называют распределением F Фишера – Снедекорасо степенями… (12.5)