Разыгрывание случайных величин.

Определение 24.1. Случайными числами называют возможные значения r непрерывной случайной величины R, распределенной равномерно в интервале (0; 1).

 

1. Разыгрывание дискретной случайной величины.

Пусть требуется разыграть дискретную случайную величину Х, то есть получить последовательность ее возможных значений, зная закон распределения Х:

Х х₁ х₂ … х_п

р р₁ р₂ … р_п .

Рассмотрим равномерно распределенную в (0, 1) случайную величину R и разобьем интервал (0, 1) точками с координатами р_1, р₁ + р₂, …, р₁ + р₂ +… +р_п-1 на п частичных интервалов , длины которых равны вероятностям с теми же индексами.

Теорема 24.1. Если каждому случайному числу , которое попало в интервал 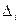, ставить в соответствие возможное значение , то разыгрываемая величина будет иметь заданный закон распределения:

Х х₁ х₂ … х_п

р р₁ р₂ … р_п .

Доказательство.

Возможные значения полученной случайной величины совпадают с множеством х₁ , х₂ ,… х_п, так как число интервалов равно п, а при попадании r_j в интервал 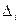случайная величина может принимать только одно из значений х₁ , х₂ ,… х_п.

Так как R распределена равномерно, то вероятность ее попадания в каждый интервал равна его длине, откуда следует, что каждому значению соответствует вероятность p_i. Таким образом, разыгрыываемая случайная величина имеет заданный закон распределения.

 

Пример. Разыграть 10 значений дискретной случайной величины Х, закон распределения которой имеет вид: Х 2 3 6 8

р 0,1 0,3 0,5 0,1

Решение. Разобьем интервал (0, 1) на частичные интервалы: D₁- (0; 0,1), D₂ – (0,1; 0,4), D₃ - (0,4; 0,9), D₄ – (0,9; 1). Выпишем из таблицы случайных чисел 10 чисел: 0,09; 0,73; 0,25; 0,33; 0,76; 0,52; 0,01; 0,35; 0,86; 0,34. Первое и седьмое числа лежат на интервале D₁, следовательно, в этих случаях разыгрываемая случайная величина приняла значение х₁ = 2; третье, четвертое, восьмое и десятое числа попали в интервал D₂, что соответствует х₂ = 3; второе, пятое, шестое и девятое числа оказались в интервале D₃ – при этом Х = х₃ = 6; на последний интервал не попало ни одного числа. Итак, разыгранные возможные значения Х таковы: 2, 6, 3, 3, 6, 6, 2, 3, 6, 3.

 

2. Разыгрывание противоположных событий.

Пусть требуется разыграть испытания, в каждом из которых событие А появляется с известной вероятностью р. Рассмотрим дискретную случайную величину Х, принимающую значения 1 (в случае, если событие А произошло) с вероятностью р и 0 (если А не произошло) с вероятностью q = 1 – p. Затем разыграем эту случайную величину так, как было предложено в предыдущем пункте.

 

Пример. Разыграть 10 испытаний, в каждом из которых событие А появляется с вероятностью 0,3.

Решение. Для случайной величины Х с законом распределения Х 1 0

р 0,3 0,7

получим интервалы D₁ – (0; 0,3) и D₂ – (0,3; 1). Используем ту же выборку случайных чисел, что и в предыдущем примере, для которой в интервал D₁ попадают числа №№1,3 и 7, а остальные – в интервал D₂. Следовательно, можно считать, что событие А произошло в первом, третьем и седьмом испытаниях, а в остальных – не произошло.

 

3. Разыгрывание полной группы событий.

Если события А₁, А₂, …, А_п, вероятности которых равны р₁ , р₂ ,… р_п, образуют полную группу, то для из разыгрывания (то есть моделирования последовательности их появлений в серии испытаний) можно разыграть дискретную случайную величину Х с законом распределения Х 1 2 … п, сделав это так же, как в пункте 1. При этом считаем, что

р р₁ р₂ … р_п

если Х принимает значение х_i = i, то в данном испытании произошло событие А_i.

 

4. Разыгрывание непрерывной случайной величины.

а) Метод обратных функций.

Пусть требуется разыграть непрерывную случайную величину Х, то есть получить последовательность ее возможных значений x_i (i = 1, 2, …, n), зная функцию распределения F(x).

Теорема 24.2. Если r_i – случайное число, то возможное значение x_i разыгрываемой непрерывной случайной величины Х с заданной функцией распределения F(x), соответствующее r_i , является корнем уравнения

F(x_i) = r_i. (24.1)

Доказательство.

Так как F(x) монотонно возрастает в интервале от 0 до 1, то найдется (причем единственное) значение аргумента x_i , при котором функция распределения примет значение r_i . Значит, уравнение (24.1) имеет единственное решение: х_i = F^-1(r_i ), где F^-1- функция, обратная к F. Докажем, что корень уравнения (24.1) является возможным значением рассматриваемой случайной величины Х. Предположим вначале, что x_i – возможное значение некоторой случайной величины x, и докажем, что вероятность попадания x в интервал (с, d) равна F(d) – F(c). Действительно, 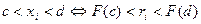в силу монотонности F(x) и того, что F(x_i) = r_i. Тогда

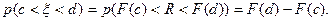, следовательно, Значит, вероятность попадания x в интервал (c, d) равна приращению функции распределения F(x) на этом интервале, следовательно, x = Х.

 

Пример.

Разыграть 3 возможных значения непрерывной случайной величины Х, распределенной равномерно в интервале (5; 8).

Решение.

F(x) = 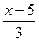, то есть требуется решить уравнение 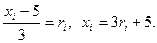Выберем 3 случайных числа: 0,23; 0,09 и 0,56 и подставим их в это уравнение. Получим соответствующие возможные значения Х:

б) Метод суперпозиции.

Если функция распределения разыгрываемой случайной величины может быть представлена в виде линейной комбинации двух функций распределения:

, (24.2)

то , так как при х®¥ F(x) ® 1.

Введем вспомогательную дискретную случайную величину Z с законом распределения

Z 1 2 . Выберем 2 независимых случайных числа r₁ и r₂ и разыграем возможное

p C₁ C₂

значение Z по числу r₁ (см. пункт 1). Если Z = 1, то ищем искомое возможное значение Х из уравнения 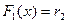, а если Z = 2, то решаем уравнение .

Можно доказать, что при этом функция распределения разыгрываемой случайной величины равна заданной функции распределения.

в) Приближенное разыгрывание нормальной случайной величины.

Так как для R, равномерно распределенной в (0, 1), , то для суммы п независимых, равномерно распределенных в интервале (0,1) случайных величин . Тогда в силу центральной предельной теоремы нормированная случайная величина при п ® ¥ будет иметь распределение, близкое к нормальному, с параметрами а = 0 и s =1. В частности, достаточно хорошее приближение получается при п = 12: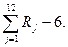

Итак, чтобы разыграть возможное значение нормированной нормальной случайной величины х, надо сложить 12 независимых случайных чисел и из суммы вычесть 6.