Однофакторный дисперсионный анализ.
Пусть генеральные совокупности Х1, Х2,…, Хр распределены нормально и имеют одинаковую дисперсию, значение которой неизвестно. Найдем выборочные средние по выборкам из этих генеральных совокупностей и проверим при заданном уровне значимо-сти нулевую гипотезу Н0: М(Х1) = М(Х2) = … = М(Хр) о равенстве всех математических ожиданий. Для решения этой задачи применяется метод, основанный на сравнении дисперсий и названный поэтому дисперсионным анализом.
Будем считать, что на случайную величину Х воздействует некоторый качественный фактор F, имеющий р уровней: F1, F2, …, Fp. Требуется сравнить «факторную дисперсию», то есть рассеяние, порождаемое изменением уровня фактора, и «остаточную дисперсию», обусловленную случайными причинами. Если их различие значимо, то фактор существенно влияет на Х и при изменении его уровня групповые средние различаются значимо.
Будем считать, что количество наблюдений на каждом уровне фактора одинаково и равно q. Оформим результаты наблюдений в виде таблицы:
| Номер испытания | Уровни фактора Fj | |||
| F1 | F2 | … | Fp | |
| … q | x11 x21 … xq1 | x12 x22 … xq2 | … … … … | x1p x2p … xqp |
| Групповое среднее | 
| 
| … | 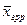
|
Определим общую, факторную и остаточную суммы квадратов отклонений от среднего:
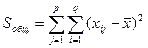 - (23.1)
- (23.1)
- общая сумма квадратов отклонений наблюдаемых значений от общего среднего  ;
;
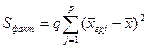 - (23.2)
- (23.2)
- факторная сумма отклонений групповых средних от общей средней, характеризующая рассеяние между группами;
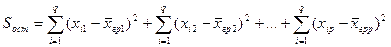 - (23.3)
- (23.3)
- остаточная сумма квадратов отклонений наблюдаемых значений группы от своего группового среднего, характеризующая рассеяние внутри групп.
Замечание. Остаточную сумму можно найти из равенства
Sост = Sобщ – Sфакт .
Вводя обозначения 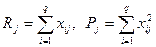 , получим формулы, более удобные для расчетов:
, получим формулы, более удобные для расчетов:
 , (23.1`)
, (23.1`)
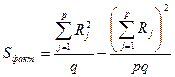 . (23.2`)
. (23.2`)
Разделив суммы квадратов на соответствующее число степеней свободы, получим общую, факторную и остаточную дисперсии:
 . (23.4)
. (23.4)
Если справедлива гипотеза Н0, то все эти дисперсии являются несмещенными оценками генеральной дисперсии. Покажем, что проверка нулевой гипотезы сводится к сравнению факторной и остаточной дисперсии по критерию Фишера-Снедекора (см. лекцию 12).
1. Пусть гипотеза Н0 правильна. Тогда факторная и остаточная дисперсии являются несмещенными оценками неизвестной генеральной дисперсии и, следовательно, различаются незначимо. Поэтому результат оценки по критерию Фишера-Снедекора F покажет, что нулевая гипотеза принимается. Таким образом, если верна гипотеза о равенстве математических ожиданий генеральных совокупностей, то верна и гипотеза о равенстве факторной и остаточной дисперсий.
2. Если нулевая гипотеза неверна, то с возрастанием расхождения между математичес-кими ожиданиями увеличивается и факторная дисперсия, а вместе с ней и отношение 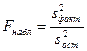 . Поэтому в результате Fнабл окажется больше Fкр, и гипотеза о равенстве дисперсий будет отвергнута. Следовательно, если гипотеза о равенстве математических ожиданий генеральных совокупностей ложна, то ложна и гипотеза о равенстве факторной и остаточной дисперсий.
. Поэтому в результате Fнабл окажется больше Fкр, и гипотеза о равенстве дисперсий будет отвергнута. Следовательно, если гипотеза о равенстве математических ожиданий генеральных совокупностей ложна, то ложна и гипотеза о равенстве факторной и остаточной дисперсий.
Итак, метод дисперсионного анализа состоит в проверке по критерию F нулевой гипотезы о равенстве факторной и остаточной дисперсий.
Замечание. Если факторная дисперсия окажется меньше остаточной, то гипотеза о равенстве математических ожиданий генеральных совокупностей верна. При этом нет необходимости использовать критерий F.
Если число испытаний на разных уровнях различно (q1 испытаний на уровне F 1, q 2 – на уровне F 2 , …, qр - на уровне F р ), то
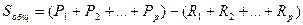 ,
,
где 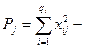 сумма квадратов наблюдавшихся значений признака на уровне Fj,
сумма квадратов наблюдавшихся значений признака на уровне Fj,
 сумма наблюдавшихся значений признака на уровне Fj . При этом объем выборки, или общее число испытаний, равен
сумма наблюдавшихся значений признака на уровне Fj . При этом объем выборки, или общее число испытаний, равен 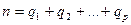 .
.
Факторная сумма квадратов отклонений вычисляется по формуле
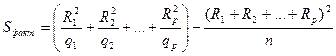 .
.
Остальные вычисления проводятся так же, как в случае одинакового числа испытаний:
 .
.