УЧЕБНО-МАТЕРИАЛЬНОЕ ОБЕСПЕЧЕНИЕ

 

 

1. Наглядные пособия: Формирующий фильтр для марковского случайного процесса.. Алгоритм фильтрации Калмана. Алгоритм оптимального управления.

2. ТСО: ___ Лектор – 2000 .________________________________________

3. Приложения: _____ Раздаточный материал.________________________

 

 

СОДЕРЖАНИЕ

Введение

К особенностям теории стохастического оптимального управления относятся: использование для описания объектов методов теории переменных состояния; использование средне-квадратических целевых функций, записанных в рекуррентной форме; фундаментальная роль принципа разделения; построение алгоритмов стохастического оценивания состояния объекта на основе фильтров Калмана; а также использование известных детерминированных методов при отыскании управляющих воздействий.

В основе постановки и решения задачи оптимального управления лежат ответы на следующие вопросы. Какой класс моделей может быть использован для описания состояния управляемых переменных и процесса функционирования стохастического объекта в целом? Какой физический смысл и математическую форму должна иметь целевая функция управления(критерий оптимальности) в условиях вероятностно – временных изменений состояния объекта? Какой метод оптимизации управляющих воздействий может быть использован для решения задачи рассматриваемого класса?

 

Вопрос№1. Проблемы векторной оптимизации процесса функционирования ТКС.

 

Качество процесса функционирования ТКС оценивается на основе сформулированной в соответствии с целью исследования системой показателей 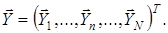Формализованная цель исследования- критерий оптимальности I_n= min L(Y,Y_тр) формулируется на основе целевой функции L(Y,Y_тр), включающей систему показателей (требований), а также указания по поиску ее экстремума (min, max, min max, max min и др.).

В настоящее время используются следующие основные виды целевых функций:

-простая ;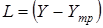

-модульная ;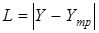

-квадратичная .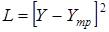

Наличие множества различных и зачастую противоречивых критериев оптимальности ТКС порождает проблему многокритериальной (векторной) оптимизации процесса ее функционирования. Основными трудностями на пути ее разрешения являются необходимость сокращения размерности векторного критерия оптимальности (ВКО), нормализации и последующей скаляризации (свертки) его компонент.

 

Редукция системы критериев оптимальности.

Уменьшение размерности системы показателей (критериев оптимальности) значительно упрощает решение задачи ВКО. Одним из наиболее распространенных методов редукции является метод, основанный на оценке степени линейной независимости отдельных компонент векторного критерия.

Вычисление матрицы коэффициентов корреляции ВКО проводится на основе следующего выражения [ ]:

M_;

=

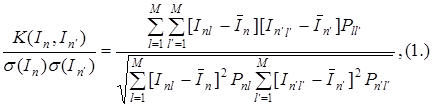
где 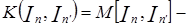матричная взаимная корреляционная функция n-го и -го критериев диагональные члены которой являются дисперсиями n-х критериев, а остальные члены характеризуют степень линейной независимости любой пары критериев;

рn,- номера критериев оптимальности;

l=1,…,M- номера дискретных значений критериев;

среднее значение критерия;

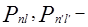вероятности принятия n(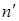)-м критерием значения l;

совместная вероятность принятия n-м критерием l-го значения и м критерием 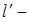го значения.

Редукция системы критериев осуществляется путем удаления из исходной системы тех критериев 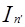, которым в матрице коэффициентов корреляции {} соответствуют такие недиагональные элементы, которые превышают величину 0,95. Следует отметить, что критерии оптимальности в исходной системе должны быть предварительно ранжированы по степени их важности для пользователя ТКС. Для случая непрерывнозначных критериев вероятности в выражении (1.) должны быть заменены на плотности распределения, а суммы на интегралы.

 

Нормализация компонент векторного критерия.

Процесс нормализации включает этапы перехода к единой размерности (безразмерности), сведения к одной точке отсчета и переход к равноценным шкалам (одному масштабу). Достаточно полно все перечисленные этапы могут быть выполнены при использовании следующего линейного преобразования:

где 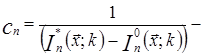масштабный коэффициент;

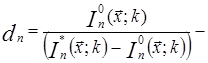коэффициент сдвига, корректирующий начало отсчета;

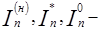нормированное, наибольшее и наименьшее значения критериев.

Использование преобразования (1.5.2.) позволяет привести все критерии к нулевой точке отсчета, их изменение ограничивается отрезком [0,1], а также делает все критерии безразмерными. Для изменения цели в критерии с max на min необходимо заменить знаки при коэффициентах c_n и d_n на обратные в выражении (1.5.2.).

 

Скаляризация (свертка) векторного критерия оптимальности.

Задача оптимизации по векторному критерию состоит в отыскании решений, удовлетворяющих экстремуму одновременно всех компонент ВКО. Существует два основных пути решения данной задачи: поиск компромиссных решений, оптимальных по Парето и поиск решений, оптимальных в смысле обобщенного скалярного критерия, полученного путем свертки (скаляризации) всех компонент ВКО. Первый путь связан с трудностями использования строгих математических методов оптимизации для широкого круга задач, а также отсутствием, как правило, единственности искомого решения[ ]. В связи с этим этап поиска компромиссных решений имеет вспомогательное значение и используется лишь для предварительного уменьшения размерности исходного множества решений до этапа свертки ВКО.

Суть второго метода заключается в сведении векторной задачи оптимизации к скалярной. При этом формируется обобщенный критерий, значение которого для различных вариантов управления является проекцией всех компонент ВКО на одну числовую ось, что значительно облегчает окончательный выбор оптимального решения, так как существует множество конструктивных скалярных методов оптимизации. К основным методам свертки ВКО ( рис.2.) относятся:

- методы, основанные на последовательной оптимизации по частным критериям (метод ведущей компоненты, оптимизация по ранжированной последовательности критериев, метод последовательных уступок, методы «Электра-1»);

- методы, основанные на получении обобщенных скалярных критериев (метод аддитивной свертки компонент ВКО с весовыми коэффициентами, метод идеальной (утопической) точки, метод вероятностной свертки).

Особенностями первой группы методов является последовательный (по всем компонентам ВКО) характер решения задачи оптимизации, что приводит к возможности потери компромиссно- оптимального решения уже на первых шагах оптимизации. Основным недостатком метода взвешенной суммы является субъективный характер выбора весовых коэффициентов определяющих важность различных компонент ВКО и, как следствие, субъективность получаемых решений.

Свободным от большинства указанных недостатков является метод идеальной точки, в котором формирование обобщенного критерия оптимальности осуществляется согласно выражению:

где q= 1,2,…- степень целевой функции;

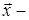вектор, оптимизируемых по ВКО параметров.

Следует отметить, что в качестве идеальных значений критериев 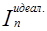могут выступать либо экстремальные значения n-х критериев, либо требования к их значениям со стороны пользователей ТКС.

Для случая стохастических систем в выражении (1.5.3.) выборочные значения критериев должны быть заменены на их средние значения 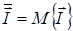. Здесь M{ . }- знак математического ожидания.

Кроме того, при наличии косвенных наблюдений за состоянием ТКС эти средние становятся условными по их выборочным значениям:

 

где среднее значение обобщенного критерия условное по наблюдениям .

 

Вопрос №2. Принцип разделения в задаче стохастического оптимального управления.

 

Сведение векторной задачи оптимизации к скалярной, выполняемой по обобщенному критерию(1.5.4), делает целесообразным рассмотрение общего подхода к решению задач скалярной динамической оптимизации [ ].

Для линейных стохастических процессов, описываемых уравнениями состояния и наблюдения вида:

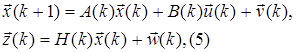
а также при квадратичном критерии оптимальности типа:

где и Q₁- неотрицательно определенные матрицы;

R₁- положительно определенная матрица. Остальные параметры имеют введенный выше смысл.

Как показано в работах [ ], для линейной постановки задачи (3,4.) справедлив принцип разделения, который разбивает решение общей стохастической динамической задачи управления на два раздельно выполняемых, но взаимоувязанных этапа:

- этап получения стохастической оптимальной оценки 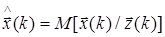состояния процесса 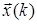на основе наблюдений ;

- этап формирования детерминированных управляющих воздействий , линейно связанных с оценкой состояния.

 

 

Вопрос №3. Алгоритм фильтрации Калмана случайных процессов и последовательностей.

 

Можно показать [ ], что для случая модели состояния и наблюдения (5.) текущая оценка, оптимальная в смысле критерия МСКО (6),может быть найдена из следующего рекуррентного алгоритма Калмана:

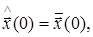
где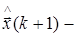оценка процесса на k+1-м шаге;

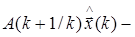предсказанное значение оценки на k+1-й шаг;

матрица коэффициентов усиления фильтра Калмана;

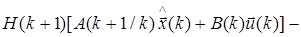измерение, предсказанное на основе прежней оценки на k+1- й шаг.

Отметим, что для линейной постановки задачи матрица коэффициентов не зависит от измеряемых сигналов, а поэтому может быть вычислена заранее в соответствии с выражением:

где R(k+1)- ковариационная матрица шумов наблюдения;

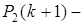ковариационная матрица (дисперсий) ошибок оценивания, определяемая следующим выражением:

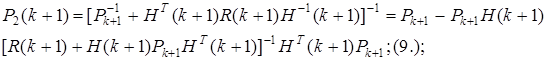
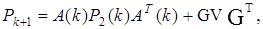(10.)-ковариационная матрица оценки с начальным условием = .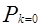

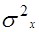Для установившегося режима работы фильтра выражения (8,9,10.) принимают вид:

K=P₂H^TR^-1;(11.)

P= A P₂A^T+ GVG^T ;(12.)

P₂(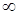)=,(12б.)

где V- ковариационная матрица шумов возбуждения, а остальные матрицы имеют ранее введенный смысл.

 

Вопрос №4. Динамическое программирование Беллмана. Принципы инвариантного погружения и оптимальности.

 

Основным методами решения задачи на втором этапе являются методы динамического программирования Беллмана. Особенностями методов динамического программирования являются использование для их реализации принципов инвариантного погружения и оптимальности. Принцип инвариантного погружения предполагает замену общей задачи на эквивалентную совокупность более простых (пошаговых) задач. Принцип оптимальности определяет возможность получения глобально-оптимальных стратегий (решений) на основе решений пошаговых задач оптимизации. Методы динамического программирования позволяют существенно сократить число анализируемых вариантов решений в процессе определения глобально-оптимального решения за счет учета априорной информации о решениях, не являющихся допустимыми, и использования информации, полученной на предыдущих шагах оптимизации.

Функция Беллмана, подлежащая минимизации, имеет вид следующего рекуррентного уравнения:

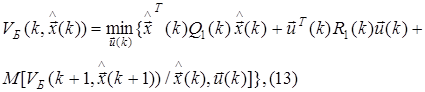
с граничным условием

Можно показать [ ], что использование данного подхода в линейном случае обеспечивает аналитический закон формирования оптимальных управляющих воздействий на k-м шаге:

где L(k)- матрица операторов управления (обратной связи).

Строгое решение задачи определения матричного оператора обратной связи для линейной и квадратичной целевой функции дано в работах [ ]. При этом полученное в них выражение для оператора имеет следующий вид:

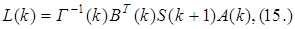
где матрица S(k) определяется рекуррентным уравнением

S(k)=

Г(k)=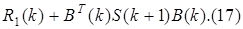

Граничное условие для момента времени k=K имеет вид: S(K)=, а остальные матрицы, входящие в выражения (14.-15.), имеют обычный смысл.