ЛИНЕЙНОЕ ПРОСТРАНСТВО

Множество 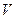элементов любой природы называется линейным или векторным пространством, а его элементы – векторами, если выполнены следующие условия.

1. Имеется операция сложения векторов, по которой каждой упорядоченной паре векторов ставится в соответствие третий вектор, что обозначается как .

2. Имеется операция умножения числа на вектор, по которой каждой упорядоченной паре из числа и вектора ставится в соответствие вектор, что обозначается как .

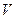3. Для любых векторов из и чисел указанные операции удовлетворяют следующим восьми аксиомам:

Сложение коммутативно, т. е. ;

Сложение ассоциативно, т. е. ;

Существует нулевой вектор 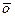такой, что для любого вектора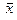выполняется ;

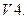Для любого вектора 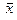существует противоположный вектортакой, что выполняется ;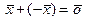

Умножение вектора на число дистрибутивноотносительно сложения чисел, т. е. ;

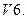Умножение вектора на число дистрибутивноотносительно сложения векторов, т. е.;

Умножение на число ассоциативно, т. е.;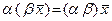

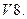При умножении на единицу вектор не изменяется, т. е. .

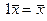Знак равенства, используемый в представленных аксиомах и во всех последующих выражениях, означает, что слева и справа от знака стоят одни и те же векторы, представленные в различных формах записи.

Подчеркнем, что, определяя линейное пространство, мы абстрагируемся как от природы изучаемых объектов, так и конкретного вида основных операций.

Таким образом, математическая структура линейной алгебры имеет вид

,

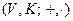причем элементы из множества 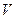называются векторами, элементы из множества 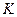являются числами (вещественными или комплексными), а операции сложения векторов и умножения числа на вектор должны удовлетворять восьми указанным выше аксиомам.

Если природа изучаемых объектов и правила выполнения двух основных операций указаны в явном виде, то соответствующее линейное пространство называют конкретным.

Рассмотрим примеры конкретных линейных пространств.

1. Множество арифметических векторов.

Всякая конечная упорядоченная последовательность из вещественных чисел называется вещественным арифметическим - мерным вектором и обозначается в виде 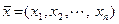. Числа называются компонентами арифметического вектора.

Сложение арифметических векторов и умножение их на число выполняется по правилам сложения соответствующих компонент и умножения каждой компоненты на число, т.е.

, .

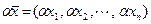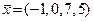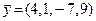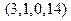Например, если даны четырехмерные арифметические векторы и , то их сумма равна вектору, а произведение вектора 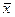на число -2 равно вектору . Так как аксиомы линейного пространства выполняются для чисел, а операци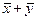и и осуществляются в виде покомпонентного сложения и умножения чисел, то и для арифметических векторов любой размерности выполняются постулаты Таким образом, множество всех вещественных арифметических -мерных векторов с введенными выше операциями есть линейное пространство, нулевым вектором которого является вектор 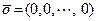, а противоположным для каждого вектора 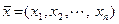является вектор 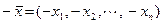. Это пространство называютвещественным - мерным арифметическим пространством и обозначают 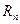.При мы получаем вещественное одномерное арифметическое пространство 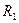,которое совпадает со множеством вещественных чисел .