Доказательство.
В соответствии с теоремой о существовании и единственности обратной матрицы, для невырожденной матрицы коэффициентов нашей системы существует единственная обратная матрица  . Умножая нашу систему, имеющую в матричной форме вид
. Умножая нашу систему, имеющую в матричной форме вид 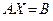 , слева на обратную матрицу
, слева на обратную матрицу  , получим:
, получим: 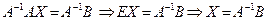 .
.
Таким образом, доказано, что матричным способом вектор – столбец решений 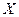 находится в единственном виде по формуле
находится в единственном виде по формуле  .
.
Если далее формулу  представить в покомпонентной записи, то для компонент
представить в покомпонентной записи, то для компонент 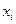 вектора неизвестных
вектора неизвестных 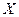 будем иметь формулы
будем иметь формулы
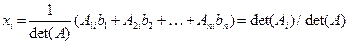 ,
,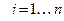 ,
,
так как суммы в круглых скобках представляют собой разложения определителей 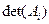 по
по  -тым столбцам матриц
-тым столбцам матриц 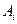 .
.
Таким образом, теорема Крамера полностью доказана.
Решим для примера следующую систему уравнений: 
Матрица коэффициентов этой системы 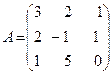 неособенная, так как
неособенная, так как 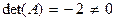 . Присоединенная матрица
. Присоединенная матрица 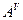 имеет вид
имеет вид 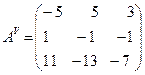 . Отсюда
. Отсюда 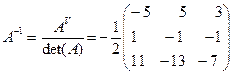 ,
, 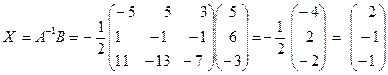 ,
,
т. е. 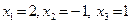 .
.
Если ту же систему уравнений решать с помощью формул Крамера, то:
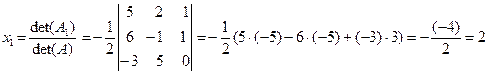 ,
,
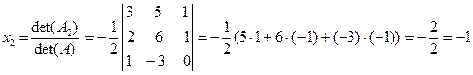 ,
,
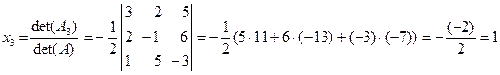 .
.
Отметим, что в нашем примере мы находили определители в числителях формул Крамера, используя разложения по столбцам свободных членов. Однако, как следует из теоремы о разложении определителя по любым строкам или столбцам, можно было выбрать любые удобные строки или столбцы.
Для исследования и решения систем линейных уравнений в общем виде введем предварительно понятие о ранге матрицы.
Пусть в матрице  размера
размера 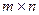 произвольно выбраны
произвольно выбраны 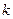 строк и
строк и 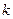 столбцов. Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу
столбцов. Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу 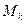 порядка
порядка 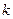 , определитель которой
, определитель которой 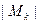 называется минором порядка
называется минором порядка 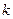 матрицы
матрицы  .
.
Базисным минором произвольной матрицы  размера
размера 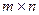 называют любой ее минор порядка
называют любой ее минор порядка 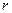 , если он отличен от нуля, а все миноры порядка
, если он отличен от нуля, а все миноры порядка  либо равны нулю, либо не существуют (выходят за размеры исходной матрицы
либо равны нулю, либо не существуют (выходят за размеры исходной матрицы  ). Порядок базисного минора называется рангом матрицы
). Порядок базисного минора называется рангом матрицы  и обозначается
и обозначается 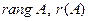 .
.
Строки и столбцы, на пересечении которых находится базисный минор, называются базисными строками и базисными столбцами.
Отметим, что у матрицы может быть несколько базисных миноров, причем каждому из них соответствуют свои базисные строки и столбцы. Если матрица  является квадратной порядка
является квадратной порядка  и невырожденной, то по определению ее ранг равен числу
и невырожденной, то по определению ее ранг равен числу  , то есть
, то есть 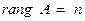 , так как определитель порядка
, так как определитель порядка  отличен от нуля, а других определителей более высокого порядка не существует. Все строки и все столбцы такой матрицы являются базисными.
отличен от нуля, а других определителей более высокого порядка не существует. Все строки и все столбцы такой матрицы являются базисными.
Если размеры 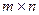 матрицы
матрицы  не очень большие, то ранг матрицы вычисляют, пользуясь методом окаймляющих миноров.
не очень большие, то ранг матрицы вычисляют, пользуясь методом окаймляющих миноров.
Пусть в матрице найден некоторый минор порядка 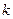 , отличный от нуля. Рассмотрим лишь те миноры порядка
, отличный от нуля. Рассмотрим лишь те миноры порядка 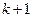 , которые содержат в себе (окаймляют) выделенный минор. Если все окаймляющие миноры равны нулю, то ранг матрицы равен
, которые содержат в себе (окаймляют) выделенный минор. Если все окаймляющие миноры равны нулю, то ранг матрицы равен 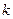 . Если же среди окаймляющих миноров найдется ненулевой минор порядка
. Если же среди окаймляющих миноров найдется ненулевой минор порядка 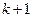 , то процедура повторяется, пока ранг не будет найден.
, то процедура повторяется, пока ранг не будет найден.
Пример.Найдем методом окаймляющих миноров ранг следующей матрицы
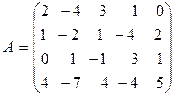 .
.
Фиксируем минор порядка два, отличный от нуля, 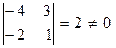 , стоящий в первых двух строках, и в третьем и четвертом столбцах матрицы.
, стоящий в первых двух строках, и в третьем и четвертом столбцах матрицы.
Минор порядка три, стоящий в левом верхнем углу, 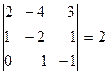 окаймляет предшествующий минор и также отличен от нуля. Однако, оба возможных окаймляющих минора порядка четыре равны нулю:
окаймляет предшествующий минор и также отличен от нуля. Однако, оба возможных окаймляющих минора порядка четыре равны нулю:
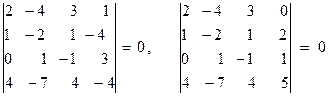 .
.
Таким образом, ранг матрицы  найден по методу окаймляющих миноров и равен трем.
найден по методу окаймляющих миноров и равен трем.
Рассмотрим далее основополагающие в линейной алгебре понятие о линейной зависимости и независимости векторов, а также определение базиса системы векторов.
Любую конечную последовательность векторов 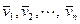 будем называть системой векторов, а любую ее подпоследовательность – подсистемой векторов. Линейной комбинацией векторов
будем называть системой векторов, а любую ее подпоследовательность – подсистемой векторов. Линейной комбинацией векторов 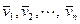 назовем вектор
назовем вектор 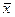 , равный сумме произведений произвольных чисел
, равный сумме произведений произвольных чисел 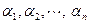 на векторы системы, т.е.
на векторы системы, т.е. 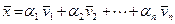 .
.
Система векторов 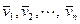 называется линейно независимой, если их линейная комбинация равна нулевому вектору только в том случае, когда все числа
называется линейно независимой, если их линейная комбинация равна нулевому вектору только в том случае, когда все числа 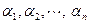 равны нулю. В обратном случае система векторов называется линейно зависимой. Отсюда, система векторов является линейно зависимой в том случае, когда линейная комбинация векторов равна нулевому вектору, а хотя бы один числовой коэффициент отличен от нуля.
равны нулю. В обратном случае система векторов называется линейно зависимой. Отсюда, система векторов является линейно зависимой в том случае, когда линейная комбинация векторов равна нулевому вектору, а хотя бы один числовой коэффициент отличен от нуля.
Линейная зависимость и независимость есть свойства системы векторов. Однако часто соответствующие прилагательные относят и к самим векторам. Поэтому вместо «линейно независимая система векторов» допустимо говорить «линейно независимые векторы».
Например, двумерные арифметические векторы 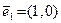 и
и 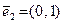 линейно независимы. Их линейная комбинация
линейно независимы. Их линейная комбинация 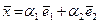 равна вектору
равна вектору 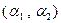 , который обращается в нулевой вектор
, который обращается в нулевой вектор 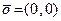 только тогда, когда
только тогда, когда 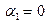 и
и 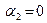 .
.
Если взять векторы 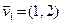 и
и 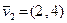 , то они являются линейно зависимыми, так как их линейная комбинация равна нулевому вектору при
, то они являются линейно зависимыми, так как их линейная комбинация равна нулевому вектору при 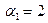 и
и 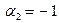 , не равных нулю.
, не равных нулю.
Из определения линейной зависимости (независимости) системы векторов вытекают следующие утверждения.
1) Если некоторая система векторов содержит нулевой вектор, то она является линейно зависимой.
Пусть для определенности первый вектор системы является нулевым, т.е. 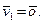
Тогда линейная комбинация векторов вида 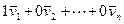 равна нулевому вектору, что и доказывает наше утверждение.
равна нулевому вектору, что и доказывает наше утверждение.
2) Если среди векторов системы есть такие, которые сами образуют линейно зависимую подсистему, то вся система также линейно зависима.
Так как исходная подсистема линейно зависима, то среди коэффициентов линейной комбинации векторов подсистемы имеется хотя бы один отличный от нуля. Добавим к этой линейной комбинацию линейную комбинацию векторов, не вошедших в исходную подсистему, с числовыми коэффициентами, равными нулю. Мы получим линейную комбинацию из векторов полной системы, которая равна нулевому вектору, причем имеется хотя бы один коэффициент отличный от нуля. Таким образом, наше утверждение доказано.
3) Если система векторов линейно независима, то и любая ее подсистема также линейно независима.
Если предположить обратное, т.е. существование некоторой линейно зависимой подсистемы, то по предыдущему утверждению отсюда следует зависимость исходной системы, что противоречит условию доказываемой теоремы. Полученное противоречие доказывает сформулированное утверждение.
4) Для того чтобы система из  ненулевых векторов была линейно зависима необходимо и достаточно, чтобы хотя бы один из векторов системы мог быть представлен как линейная комбинация предшествующих векторов.
ненулевых векторов была линейно зависима необходимо и достаточно, чтобы хотя бы один из векторов системы мог быть представлен как линейная комбинация предшествующих векторов.
Необходимость.Пусть система векторов 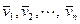 линейно зависима. Тогда равенство
линейно зависима. Тогда равенство 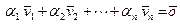 выполняется при том условии, что хотя бы одно из чисел в левой части равенства отлично от нуля. Будем перебирать эти числа, начиная с большего номера, и остановимся на некотором номере
выполняется при том условии, что хотя бы одно из чисел в левой части равенства отлично от нуля. Будем перебирать эти числа, начиная с большего номера, и остановимся на некотором номере 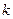 таком, что соответствующий коэффициент отличен от нуля, т.е.
таком, что соответствующий коэффициент отличен от нуля, т.е. 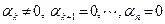 . Номер
. Номер 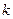 не может быть равен единице, так как иначе из условий
не может быть равен единице, так как иначе из условий 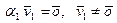 и теоремы о нулевом произведении следовало бы равенство
и теоремы о нулевом произведении следовало бы равенство 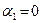 , что противоречит правилу выбора номера
, что противоречит правилу выбора номера 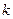 и условию теоремы. Таким образом
и условию теоремы. Таким образом 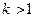 , и справедливо равенство
, и справедливо равенство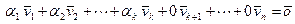 . Отсюда находим вектор
. Отсюда находим вектор 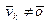 таким образом, чтобы он является линейной комбинацией предшествующих ему векторов, а именно
таким образом, чтобы он является линейной комбинацией предшествующих ему векторов, а именно 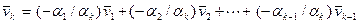 .
.
Достаточность.Пусть имеется некоторый вектор 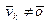 , который представлен в виде линейной комбинации предшествующих ему векторов
, который представлен в виде линейной комбинации предшествующих ему векторов 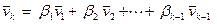 . Тогда выполняется условие
. Тогда выполняется условие 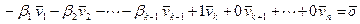 , что по определению означает линейную независимость исходной системы векторов.
, что по определению означает линейную независимость исходной системы векторов.
По аналогичной схеме доказывается следующее утверждение.
5) Система векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов системы может быть представлен в виде линейной комбинации остальных векторов.