Доказательство.
Покажем достаточность условия второго следствия. Если строки матрицы линейно зависимы, то по свойству системы зависимых векторов одна из строк является линейной комбинацией остальных строк. Вычитая из этой строки указанную линейную комбинацию, мы, не изменяя величины определителя, получим матрицу, содержащую нулевую строку. Определитель такой матрицы всегда равен нулю, что и требовалось доказать.
Покажем, что условие линейной зависимости столбцов квадратной матрицы является необходимымдля равенства нулю определителя матрицы. Если определитель порядка  равен нулю, то его базисный минор имеет порядок, заведомо меньший
равен нулю, то его базисный минор имеет порядок, заведомо меньший  . Но тогда хотя бы одна из строк является не базисной. По теореме о базисном миноре эта строка может быть представлена в виде линейной комбинации базисных строк, что и означает линейную зависимость всех строк исходной матрицы. Следствие полностью доказано.
. Но тогда хотя бы одна из строк является не базисной. По теореме о базисном миноре эта строка может быть представлена в виде линейной комбинации базисных строк, что и означает линейную зависимость всех строк исходной матрицы. Следствие полностью доказано.
Если размеры 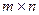 матрицы
матрицы  большие, то ранг матрицы вычисляют, пользуясь методом элементарных преобразований. Этот метод является универсальным и используется также для исследования и решения систем уравнений, вычисления определителей и обращения матриц.
большие, то ранг матрицы вычисляют, пользуясь методом элементарных преобразований. Этот метод является универсальным и используется также для исследования и решения систем уравнений, вычисления определителей и обращения матриц.
Элементарными преобразованиями матрицы называют следующие:
1) перестановка строк (столбцов) матрицы;
2) умножение строки (столбца) на число отличное от нуля;
3) прибавление к элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.
Целью элементарных преобразований является приведение исходной матрицы к ступенчатой форме. Матрица называется ступенчатой, если для нее выполняются следующие условия:
1) если какая – либо строка матрицы состоит из нулей, то и все последующие строки также состоят из нулей;
2) если первый, отличный от нуля, элемент какой – либо строки расположен в одном из столбцов данной матрицы, то все элементы этого столбца, расположенные ниже, являются нулевыми.
Матрица из одной строки считается ступенчатой по определению.
Например, матрица 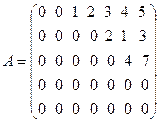 является ступенчатой.
является ступенчатой.