Доказательство.
Ранг матрицы коэффициентов системы 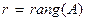 по определению всегда меньше или равен числа уравнений или числа неизвестных исходной системы:
по определению всегда меньше или равен числа уравнений или числа неизвестных исходной системы: 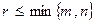 . Ранг расширенной матрицы за счет добавления одного столбца правой части системы может быть на единицу большим. Таким образом, для рангов рассматриваемых матриц всегда выполняется условие
. Ранг расширенной матрицы за счет добавления одного столбца правой части системы может быть на единицу большим. Таким образом, для рангов рассматриваемых матриц всегда выполняется условие 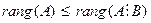 . Выполнив конечное число элементарных преобразований в соответствии с прямым ходом метода Гаусса, приведем расширенную матрицу системы к стандартному ступенчатому виду
. Выполнив конечное число элементарных преобразований в соответствии с прямым ходом метода Гаусса, приведем расширенную матрицу системы к стандартному ступенчатому виду
 .
.
С точностью до обозначения неизвестных, полученной ступенчатой матрице соответствует ступенчатая система уравнений, равносильная исходной системе. Назовем неизвестные, стоящие в первых 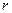 столбцах преобразованной матрицы базисными и обозначим их для конкретности как
столбцах преобразованной матрицы базисными и обозначим их для конкретности как  . Оставшиеся неизвестные общим числом
. Оставшиеся неизвестные общим числом 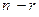 , назовем свободными и обозначим
, назовем свободными и обозначим 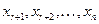 . Отметим, что свободные переменные появятся только в том случае, когда ранг матрицы коэффициентов строго меньше числа неизвестных.
. Отметим, что свободные переменные появятся только в том случае, когда ранг матрицы коэффициентов строго меньше числа неизвестных.
Покажем необходимость условия теоремы, т. е. положим, что система совместна и докажем, что  . Если система совместна, то в
. Если система совместна, то в 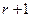 -ой строке полученной ступенчатой матрицы число
-ой строке полученной ступенчатой матрицы число  должно быть равно нулю. Иначе в уравнении, соответствующем этой строке, слева от знака равенства стоит число, равное нулю, а справа стоит число отличное от нуля. Таким образом, число ненулевых строк в преобразованной расширенной матрице равно
должно быть равно нулю. Иначе в уравнении, соответствующем этой строке, слева от знака равенства стоит число, равное нулю, а справа стоит число отличное от нуля. Таким образом, число ненулевых строк в преобразованной расширенной матрице равно 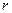 и по теореме о ранге матриц выполняются условия
и по теореме о ранге матриц выполняются условия  . Так как элементарные преобразования над расширенной матрицей не изменили ее ранга, то справедливо равенство
. Так как элементарные преобразования над расширенной матрицей не изменили ее ранга, то справедливо равенство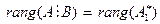 , и, следовательно
, и, следовательно  , что и требовалось доказать.
, что и требовалось доказать.
Покажем достаточность условия теоремы, т. е. положим, что  и докажем, что система совместна. Воспользуемся логическим законом контрпозиции и докажем утверждение, равносильное исходному утверждению: «если система несовместна, то
и докажем, что система совместна. Воспользуемся логическим законом контрпозиции и докажем утверждение, равносильное исходному утверждению: «если система несовместна, то  ». Если система несовместна, то в
». Если система несовместна, то в 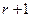 -ой строке, полученной ступенчатой матрицы, число
-ой строке, полученной ступенчатой матрицы, число  должно быть отличным от нуля. Таким образом, число ненулевых строк в преобразованной расширенной матрице
должно быть отличным от нуля. Таким образом, число ненулевых строк в преобразованной расширенной матрице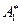 равно
равно  , и по теореме о ранге матриц выполняются условия
, и по теореме о ранге матриц выполняются условия . Так как ранг матрицы коэффициентов системы равен
. Так как ранг матрицы коэффициентов системы равен 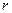 , то справедливо
, то справедливо  , что доказывает достаточность условия теоремы.
, что доказывает достаточность условия теоремы.
Таким образом, теорема Кронекера – Капелли полностью доказана.
Элементарные преобразования расширенной матрицы системы по методу Гаусса, использованные при доказательстве теоремы Кронекера – Капелли, позволяют эффективно исследовать и решать любые линейные системы.
Пример.Исследуем следующую систему уравнений:
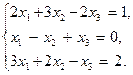
Расширенная матрица этой системы имеет вид
 .
.
Первые три столбца этой матрицы образуют матрицу  коэффициентов системы. Проводя элементарные преобразования расширенной матрицы, мы одновременно проводим соответствующие элементарные преобразования матрицы коэффициентов системы. Преобразуем расширенную матрицу системы в соответствии с прямым ходом метода Гаусса: переставим первую и вторую строки; последовательно умножим новую первую строку на (-2) и на (-3) и сложим со второй и третьей строками; из третьей строки вычтем вторую и затем разделим вторую строку на число 5
коэффициентов системы. Проводя элементарные преобразования расширенной матрицы, мы одновременно проводим соответствующие элементарные преобразования матрицы коэффициентов системы. Преобразуем расширенную матрицу системы в соответствии с прямым ходом метода Гаусса: переставим первую и вторую строки; последовательно умножим новую первую строку на (-2) и на (-3) и сложим со второй и третьей строками; из третьей строки вычтем вторую и затем разделим вторую строку на число 5
 .
.
Третье уравнение преобразованной по методу Гаусса системы, которое соответствует третьей строке преобразованной расширенной матрицы, не имеет решения. Поэтому не имеет решений (несовместна) и равносильная ей исходная система уравнений. При этом преобразованная матрица коэффициентов системы имеет две ненулевых строки и соответственно 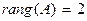 , а преобразованная расширенная матрица имеет три ненулевых строки и
, а преобразованная расширенная матрица имеет три ненулевых строки и 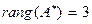 . Таким образом, условия теоремы Кронекера – Капелли не выполняются и исходная система из трех уравнений с тремя неизвестными – несовместна.
. Таким образом, условия теоремы Кронекера – Капелли не выполняются и исходная система из трех уравнений с тремя неизвестными – несовместна.
Следствие 1. Если система линейных уравнений совместна ( ) и число неизвестных системы равно рангу матрицы системы
) и число неизвестных системы равно рангу матрицы системы 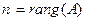 , то система уравнений всегда имеет единственное решение.
, то система уравнений всегда имеет единственное решение.
Доказательство.Действительно, если условия следствия выполняются, то в 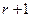 -ой строке полученной ступенчатой матрицы
-ой строке полученной ступенчатой матрицы 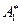 число
число  равно нулю, так что в матрице
равно нулю, так что в матрице 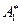 (
(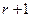 ) -ая строка и все последующие (если эти строки имеются) являются нулевыми. Уравнения, отвечающие нулевым строкам, не влияют на множество решений и их можно не включать в преобразованную систему. Таким образом, независимо от числа уравнений
) -ая строка и все последующие (если эти строки имеются) являются нулевыми. Уравнения, отвечающие нулевым строкам, не влияют на множество решений и их можно не включать в преобразованную систему. Таким образом, независимо от числа уравнений 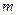 в исходной системе, равносильная ей система уравнений, отвечающая ступенчатой матрице
в исходной системе, равносильная ей система уравнений, отвечающая ступенчатой матрице 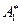 , является квадратной и невырожденной. По теореме Крамера такая система имеет единственное решение, что и требовалось доказать.
, является квадратной и невырожденной. По теореме Крамера такая система имеет единственное решение, что и требовалось доказать.
Отметим, что указанное в следствие единственное решение не обязательно искать по формулам Крамера. Более экономно продолжить преобразования матрицы 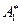 , отбросив предварительно нулевые строки, и выполнить обратный ход метода Гаусса.
, отбросив предварительно нулевые строки, и выполнить обратный ход метода Гаусса.
Пример.Решим методом Гаусса следующую систему уравнений:
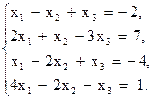
Выпишем расширенную матрицу этой системы и выполним ее элементарные преобразования по методу Гаусса. Умножим первую строку последовательно на числа 2, 1, 4 и вычтем результаты соответственно из второй, третьей и четвертой строк; далее третью строку умножим на число (-1) и переставим вторую и третью строки местами:

Умножим теперь вторую строку на числа 3, 2 и вычтем результат последовательно из третьей и четвертой строк; из четвертой строки вычтем третью, а третью строку разделим на (-5).
 .
.
На этом заканчивается прямой ход метода Гаусса. Анализируя полученную ступенчатую матрицу, можно сделать вывод о том, что и в преобразованной матрице коэффициентов, и в преобразованной расширенной матрице имеются по три ненулевых строки, так что 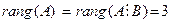 . Число неизвестных в решаемой системе также равно трем, так что по следствию 1 исследуемая система имеет единственное решение. Это решение найдем, выписав систему уравнений, соответствующую ступенчатой матрице
. Число неизвестных в решаемой системе также равно трем, так что по следствию 1 исследуемая система имеет единственное решение. Это решение найдем, выписав систему уравнений, соответствующую ступенчатой матрице 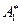 :
:

и выполняя обратный ход метода Гаусса. Для этого последовательно определим неизвестные, начиная с последнего уравнения и выполняя необходимые подстановки. Таким образом: 
Следствие 2. Если система линейных уравнений совместна ( ) и ранг матрицы системы
) и ранг матрицы системы  строго меньше числа неизвестных системы:
строго меньше числа неизвестных системы: 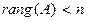 , то система уравнений всегда имеет бесконечно много решений.
, то система уравнений всегда имеет бесконечно много решений.
Действительно, если условия следствия выполняются, то отбросим в ступенчатой матрице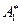 нулевые строки, которые не влияют на множество решений. Далее представим систему уравнений, отвечающую матрице
нулевые строки, которые не влияют на множество решений. Далее представим систему уравнений, отвечающую матрице 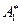 , в следующем виде:
, в следующем виде:

В этой системе слагаемые с базисными неизвестными  оставлены в левых частях уравнений, а слагаемые со свободными неизвестными
оставлены в левых частях уравнений, а слагаемые со свободными неизвестными 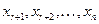 перенесены со знаком минус в правые части. Отметим, что разделение неизвестных на базисные и свободные возможно и в других комбинациях. В каждом случае получится одно и то же множество решений, представленное в различных формах записи. Обязательно только, чтобы неизвестные, выбранные как базисные, находились на пересечении базисных строк и базисных столбцов матрицы
перенесены со знаком минус в правые части. Отметим, что разделение неизвестных на базисные и свободные возможно и в других комбинациях. В каждом случае получится одно и то же множество решений, представленное в различных формах записи. Обязательно только, чтобы неизвестные, выбранные как базисные, находились на пересечении базисных строк и базисных столбцов матрицы 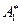 . Так как ранг матрицы
. Так как ранг матрицы 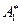 равен
равен 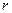 , то определитель матрицы коэффициентов, представленной системы, отличен от нуля и по теореме Крамера при любых значениях правых частей, система имеет единственное решение относительно базисных неизвестных. Свободные неизвестные могут принимать любые числовые значения и при записи общего решения исходной системы уравнений их полагают равными произвольным постоянным, так что
, то определитель матрицы коэффициентов, представленной системы, отличен от нуля и по теореме Крамера при любых значениях правых частей, система имеет единственное решение относительно базисных неизвестных. Свободные неизвестные могут принимать любые числовые значения и при записи общего решения исходной системы уравнений их полагают равными произвольным постоянным, так что  . Базисные неизвестные находятся из представленной выше системы либо по формулам Крамера, либо по полной схеме метода Гаусса, и зависят от правых частей системы
. Базисные неизвестные находятся из представленной выше системы либо по формулам Крамера, либо по полной схеме метода Гаусса, и зависят от правых частей системы 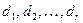 и произвольных постоянных:
и произвольных постоянных:

Отметим, что формулы, выражающие все  неизвестных
неизвестных  в виде функций от
в виде функций от 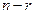 произвольных постоянных
произвольных постоянных 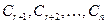 , называют общим решением исходной системы. Напомним, что множество всех решений системы также обычно называют общим решением системы уравнений, и оно совпадает с общим решением, представленным с помощью произвольных постоянных.
, называют общим решением исходной системы. Напомним, что множество всех решений системы также обычно называют общим решением системы уравнений, и оно совпадает с общим решением, представленным с помощью произвольных постоянных.