Доказательство.
Необходимость.Пусть 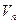 есть конечномерное пространство размерности
есть конечномерное пространство размерности  ,
,  есть произвольная линейно независимая система векторов из этого пространства, а
есть произвольная линейно независимая система векторов из этого пространства, а 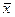 есть любой вектор из
есть любой вектор из 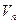 . По определению базиса достаточно показать, что вектор
. По определению базиса достаточно показать, что вектор 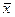 может быть разложен по векторам этой системы. Согласно определению размерности линейного пространства система, содержащая
может быть разложен по векторам этой системы. Согласно определению размерности линейного пространства система, содержащая 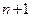 вектор,
вектор, 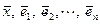 линейно зависима.
линейно зависима.
Тогда по определению линейной зависимости векторов справедливо равенство  , причем среди коэффициентов линейной комбинации в правой части равенства имеется хотя бы один не равный нулю. Коэффициент
, причем среди коэффициентов линейной комбинации в правой части равенства имеется хотя бы один не равный нулю. Коэффициент 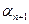 не может быть равен нулю, так как в обратном случае получается, что векторы
не может быть равен нулю, так как в обратном случае получается, что векторы  являются линейно зависимыми. Поэтому можно разделить полученное равенство на
являются линейно зависимыми. Поэтому можно разделить полученное равенство на 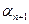 и получить разложение вектора
и получить разложение вектора 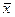 в виде:
в виде:  . Таким образом, мы получили, что векторы
. Таким образом, мы получили, что векторы  образуют базис пространства
образуют базис пространства  - мерного линейного пространства, что и требовалось доказать.
- мерного линейного пространства, что и требовалось доказать.
Достаточность. Пусть векторы  образуют базис некоторого линейного пространства. По определению размерности пространства требуется доказать, что любая система
образуют базис некоторого линейного пространства. По определению размерности пространства требуется доказать, что любая система  , содержащая
, содержащая 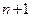 вектор, линейно зависима.
вектор, линейно зависима.
Разложим эти векторы по исходному базису в следующем виде:

Далее составим линейную комбинацию векторов  с коэффициентами
с коэффициентами 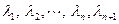 в виде
в виде  , приравняем ее нулевому вектору и сгруппируем коэффициенты при каждом из векторов
, приравняем ее нулевому вектору и сгруппируем коэффициенты при каждом из векторов  :
:
 =
= 

Так как векторы  линейно независимы, то коэффициенты при каждом из них в нашем равенстве должны быть равны нулю. Отсюда, получается линейная, однородная система из
линейно независимы, то коэффициенты при каждом из них в нашем равенстве должны быть равны нулю. Отсюда, получается линейная, однородная система из  уравнений относительно коэффициентов
уравнений относительно коэффициентов 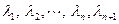 в следующем виде:
в следующем виде:

Однородная система уравнений имеет нетривиальное решение, если ранг матрицы коэффициентов строго меньше числа неизвестных. В нашем случае матрица коэффициентов имеет размеры  , а ранг любой матрицы всегда меньше наибольшего из ее размеров, так что
, а ранг любой матрицы всегда меньше наибольшего из ее размеров, так что  . Таким образом, среди наборов чисел
. Таким образом, среди наборов чисел 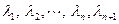 всегда имеется хотя бы один отличный от нулевого, что и доказывает достаточность условия теоремы.
всегда имеется хотя бы один отличный от нулевого, что и доказывает достаточность условия теоремы.