ВЕКТОРНАЯ АЛГЕБРА
Под векторной алгеброй обычно понимают раздел линейной алгебры, изучающий геометрические векторы на плоскости и реальном пространстве. В математике и ее приложениях встречаются различные величины. Некоторые из них (длина, площадь, объем, масса тела) полностью определяются вещественным числом. Такие величины называют скалярными величинами или скалярами. Для определения других величин необходимо указать не только числовое значение, но и присущее им направление. К таким величинам относятся сила, скорость, ускорение и так далее. Такого рода величины в математике моделируются направленными отрезками и геометрическими векторами.
В данном разделе изучаются геометрические векторы на плоскости и реальном пространстве. Предварительно приведем необходимые определения и теоремы, справедливые для любых линейных пространств.
Определение. Два линейных пространства 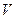 и
и  называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие, согласованное с основными операциями в этих пространствах, таким образом, что если два любых элемента
называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие, согласованное с основными операциями в этих пространствах, таким образом, что если два любых элемента  из
из 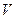 преобразуются в
преобразуются в 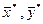 из
из  , то их сумма
, то их сумма  преобразуется в
преобразуется в 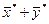 , а произведение любого числа на вектор
, а произведение любого числа на вектор 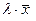 преобразуется в
преобразуется в 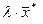 .
.
По существу, два изоморфных пространства ничем не отличаются друг от друга. Для конечномерных пространств этот факт устанавливается следующей теоремой.
Теорема (об изоморфизме).Любое  - мерное линейное пространство
- мерное линейное пространство 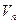 изоморфно арифметическому пространству
изоморфно арифметическому пространству 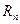 .
.
Доказательство. Как следует из определения изоморфизма, необходимо вначале установить взаимно однозначное соответствие между векторами из 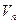 и
и 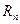 . Зафиксируем какой- либо базис в пространстве
. Зафиксируем какой- либо базис в пространстве 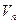 , например
, например 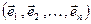 , и разложим произвольный вектор
, и разложим произвольный вектор  из
из 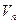 по этому базису:
по этому базису:  . Вектору
. Вектору  из
из 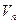 поставим в соответствие арифметический вектор
поставим в соответствие арифметический вектор 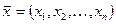 из
из 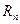 . Обратно, каждому арифметическому вектору
. Обратно, каждому арифметическому вектору 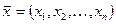 из
из 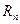 поставим в соответствие вектор
поставим в соответствие вектор 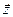 из
из 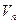 с координатами
с координатами  в базисе
в базисе 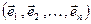 . В силу единственности разложения вектора по базису, векторы
. В силу единственности разложения вектора по базису, векторы  и
и 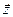 совпадают, т.е. взаимно однозначное соответствие установлено.
совпадают, т.е. взаимно однозначное соответствие установлено.
Согласованность операций сложения векторов и умножения вектора на число с данным соответствием проверяется непосредственно по теореме о свойствах координат вектора.
Поскольку при доказательстве теоремы пространство было выбрано произвольно, то и любые два пространства одинаковой размерности изоморфны между собой. Отсюда следует очень важный вывод о том, что для изучения свойств любых конечномерных пространств достаточно рассмотреть соответствующее арифметическое пространство 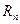 .
.